安徽省滁州市定远县民族中学2021-2022学年七年级下学期期中考试数学试题(word解析版)
文档属性
| 名称 | 安徽省滁州市定远县民族中学2021-2022学年七年级下学期期中考试数学试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 322.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-11 20:12:46 | ||
图片预览




文档简介
2021-2022学年度第二学期七年级期中考试卷
数学试题
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列说法中正确的是
A.的平方根是 B.1的立方根是
C. D.是5的平方根的相反数
2.下列各数中:3.1415926,-π,,,0.131 131 113…(每两个3之间依次多一个1),,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列实数中,最小的正数是( )
A.10-3 B.3-10 C.51-10 D.18-5
4.若,则下列各式不成立的是( )
A. B. C. D.
5.不等式组的解集在数轴上表示正确的是( )
A.B.C.D.
6.下列运算正确的是( )
A. B.
C. D.
7.如果a<b,那么下列不等式成立的是( )
A.-3a>-3b B.a-3>b-3 C. D.a-b >0
8.若am=4,an=3,则a2m+n的值为( )
A.7 B.12 C.24 D.48
9.如果,那么a,b,c三数的大小为( )
A. B. C. D.
10.若关于的一元一次不等式组无解,且方程的解是非负数,则满足条件的整数的值有( )个.
A.1 B.2 C.3 D.4
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构,使用此技术测定细菌蛋白结构的分辨率达到0.22纳米,也就是0.00000000022米.将0.00000000022用科学记数法表示为 _____.
12.若实数x、y满足,则以x、y的值为边长的等腰三角形的周长为_____.
13.已知某正数的两个平方根分别是和,b的立方根是,求_________.
14.已知是方程ax﹣2y=2的一个解,那么a的值是___.
三、解答题(本大题共8小题,满分90分)
15.(5分)计算:.
16.(6分)先化简,再求值:,其中,.
17.(8分)解不等式组,并把解集在数轴上表示出.
18.(8分)已知的立方根是3,的算术平方根是4,是的整数部分.
(1)求,,的值;
(2)求的平方根.
19.(12分)观察下列一组等式:
(1)以上这些等式中,你有何发现?利用你的发现填空.
①__________;
②( );
③( ).
(2)利用你发现的规律来计算:.
20.(12分)阅读:我们知道,于是要解不等式,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当,即时:
解这个不等式,得:
由条件,有:
(2)当,即时,
解这个不等式,得:
由条件,有:
∴如图,综合(1)、(2)原不等式的解为
根据以上思想,请探究完成下列2个小题:
(1);
(2).
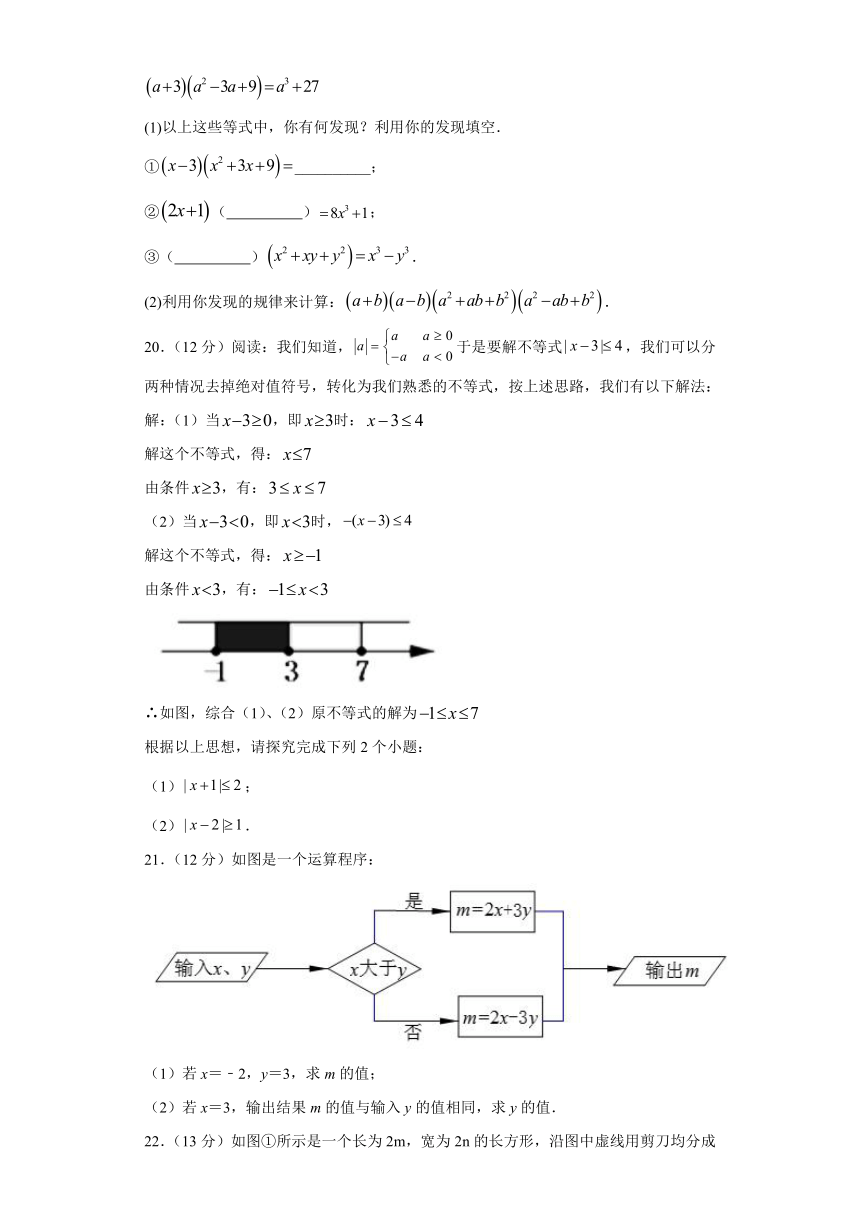
21.(12分)如图是一个运算程序:
(1)若x=﹣2,y=3,求m的值;
(2)若x=3,输出结果m的值与输入y的值相同,求y的值.
22.(13分)如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1: ;
方法2: ;
③观察图②,直接写出三个代数式(m+n)2,(m﹣n)2, mn之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若m+n=6,mn=4,求(m﹣n)2的值.
23.(14分)某公司有A,B两种型号的客车共15辆,它们的载客量、每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
型号客车 型号客车
载客量(人/辆)
租金(元/辆)
车辆数(辆)
(1)求表中a,b的值;
(2)某中学计划租用A,B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元
①求最多能租用多少辆A型客车?
②若七年级的师生共有195人,请写出所有可能的租车方案
参考答案
1.A
【解析】A、,9的平方根是,故A选项正确;
B、1的立方根是它本身1,故B选项错误;
C、,故C选项错误;
D、是5的一个平方根,故D选项错误,故选A.
2.C
【解析】无理数有:-π,,0.131131113…(每两个3之间依次多一个1),共3个.
故选C.
3.C
【解析】∵,,
∴A.,
B.,
C.,
D.,
综上所述,最小的正数是0.01,故选:C.
4.D
【解析】A、根据不等式的性质(2),不等式两边同乘以3,不等号的方向不变.故该选项成立;
B、根据不等式的性质(1),不等式两边同加上5,不等号的方向不变.故该选项成立;
C、根据不等式的性质(1)和(2),不等式的两边同乘以,再同减去1,不等号的方向不变.故该选项成立;
D、根据不等式的性质(1)和(3),不等式两边同乘以-1,则不等号的方向改变,再同加上
5.B
【解析】
解不等式①得:,
解不等式②得:,
∴不等式组的解集是,
解集在数轴上表示如图:
故选B.
6.D
【解析】A、x2、x3不是同类项,不能合并运算,故此选项错误;
B、,故此选项错误;
C、,故此选项错误;
D、,故此选项正确,故选:D.
7.A
【解析】根据不等式的基本性质1可得,选项B、D错误;
根据不等式的基本性质1,2可得,选项C错误;
根据不等式的基本性质3可得,选项A正确.故选A.
8.D
【解析】∵am=4,an=3,
∴a2m+n=(am)2×an=42×3=48.
故选:D.
9.C
【解析】, ,,
∴,故选C.
10.C
【解析】
,
由①得:x>a,
由②得:x<1,
由于不等式组无解,
所以a≥1;
解方程得
x=,
由方程的解是非负数,则有
≥0,
解得:a≤,
所以a的取值范围为1≤a≤,
所以满足条件的整数a为1、2、3,共3个,故选C.
11.2.2×10-10
【解析】0.000 000 000 22=2.2×10-10,
故答案为:2.2×10-10.
12.18或21.
【解析】根据题意得,x﹣5=0,y﹣8=0,
解得x=5,y=8,
①5是腰长时,三角形的三边分别为5、5、8,
∵5+5>8,
∴能组成三角形,周长为18;
②5是底边时,三角形的三边分别为5、8、8,
能组成三角形,
周长=8+8+5=21.
综上所述,等腰三角形的周长是18或21.
故答案为18或21.
13.20
【解析】∵某正数的两个平方根分别是a+3和2a-15,b的立方根是-2,
∴a+3+2a-15=0,b=(-2)3=8,
解得,3a=12,b=8,
∴;故答案为:20.
14.4
【解析】根据题意,将x=3,y=5代入方程得:3a﹣10=2,
解得:a=4,
故答案为:4.
15.5﹣π
【解析】原式=4﹣1﹣(π﹣3)+(﹣1)
=3﹣π+3﹣1
=5﹣π.
16.2x-3y;7.
【解析】原式=(4x2-y2-6xy+y2)÷(2x)
=(4x2-6xy) ÷(2x)
=2x-3y
当x=2,y=-1时,原式=4+3=7.
17. 解:解不等式x-3(x-2)≥4,得:x≤1,
解不等式得:x<4,
则不等式组的解集为x≤1,
将不等式组的解集表示在数轴上如下:
18.(1),,;(3)
【解析】
(1)∵的立方根是3,的算术平方根是4,
∴,,
∴,;
∵,是的整数部分,
∴;
(2)当,,时,
,16的平方根是
∴的平方根是.
19.(1)①;②;③
(2)
【解析】(1)①(x 3)(x2+3x+9)=x3 27;
②(2x+1)(4x2 2x+1)=8x3+1;
③(x y)(x2+xy+y2)=x3 y3.
故答案为①;②;③;
(2)原式
20.(1)-3≤x≤1;(2)x≥3或x≤1.
【解析】(1)|x+1|≤2,
①当x+1≥0,即x≥-1时:x+1≤2,
解这个不等式,得:x≤1
由条件x≥-1,有:-1≤x≤1;
②当x+1<0,即 x<-1时:-(x+1)≤2
解这个不等式,得:x≥-3
由条件x<-1,有:-3≤x<-1
∴综合①、②,原不等式的解为:-3≤x≤1.
(2)|x-2|≥1
①当x-2≥0,即x≥2时:x-2≥1
解这个不等式,得:x≥3
由条件x≥2,有:x≥3;
②当x-2<0,即 x<2时:-(x-2)≥1,
解这个不等式,得:x≤1,
由条件x<2,有:x≤1,
∴综合①、②,原不等式的解为:x≥3或x≤1.
21.(1)-13;(2)
【解析】(1)∵,,,
∴,
∴;
(2)∵,输出结果m的值与输入y的值相同,
∴,
①当时,
∴,
∴,
解得,符合题意;
②当时,
∴,
∴,
∴,
解得,不符合题意;
∴.
22.(1)①;②,,③;(2)20.
【解析】(1)①观察图②中的阴影部分的正方形的边长为:m﹣n.
故答案为m﹣n;
②两种不同的方法表示图②中阴影部分的面积:
方法1:;
方法2: -4mn
故答案为: 、-4mn;
③观察图②,三个代数式,,mn之间的等量关系:
=-4mn
故答案为: =-4mn;
(2)根据(1)题中的等量关系:
把m+n=6,mn=4代入: =-4mn
∴=36-16=20.
答:的值为20.
23.(1);(2)①最多能租用4辆A型客车;②所有的租车方案为:方案一:租用A种型号的客车3辆,租用B种型号的客车2辆;方案二:租用A种型号的客车4辆,租用B种型号的客车1辆
【解析】(1)由题意得:,
解得:,
即;
(2)①设计划租用A种型号客车x辆,则计划租用B种型号客车(5﹣x)辆,
根据题意得:400x+280(5﹣x)≤1900,
解得:x≤,
∵x为正整数,
∴x最大取4,
故最多能租用4辆A型客车;
②根据题意得:45x+30(5﹣x)≥195,
解得:x≥3,
∵x取正整数,
∴x=3、4,
故所有的租车方案为
方案一:租用A种型号的客车3辆,租用B种型号的客车2辆;
方案二:租用A种型号的客车4辆,租用B种型号的客车1辆.
数学试题
第I卷(选择题 40分)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列说法中正确的是
A.的平方根是 B.1的立方根是
C. D.是5的平方根的相反数
2.下列各数中:3.1415926,-π,,,0.131 131 113…(每两个3之间依次多一个1),,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列实数中,最小的正数是( )
A.10-3 B.3-10 C.51-10 D.18-5
4.若,则下列各式不成立的是( )
A. B. C. D.
5.不等式组的解集在数轴上表示正确的是( )
A.B.C.D.
6.下列运算正确的是( )
A. B.
C. D.
7.如果a<b,那么下列不等式成立的是( )
A.-3a>-3b B.a-3>b-3 C. D.a-b >0
8.若am=4,an=3,则a2m+n的值为( )
A.7 B.12 C.24 D.48
9.如果,那么a,b,c三数的大小为( )
A. B. C. D.
10.若关于的一元一次不等式组无解,且方程的解是非负数,则满足条件的整数的值有( )个.
A.1 B.2 C.3 D.4
第II卷(非选择题110分)
二、填空题(本大题共4小题,每小题5分,满分20分)
11.科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构,使用此技术测定细菌蛋白结构的分辨率达到0.22纳米,也就是0.00000000022米.将0.00000000022用科学记数法表示为 _____.
12.若实数x、y满足,则以x、y的值为边长的等腰三角形的周长为_____.
13.已知某正数的两个平方根分别是和,b的立方根是,求_________.
14.已知是方程ax﹣2y=2的一个解,那么a的值是___.
三、解答题(本大题共8小题,满分90分)
15.(5分)计算:.
16.(6分)先化简,再求值:,其中,.
17.(8分)解不等式组,并把解集在数轴上表示出.
18.(8分)已知的立方根是3,的算术平方根是4,是的整数部分.
(1)求,,的值;
(2)求的平方根.
19.(12分)观察下列一组等式:
(1)以上这些等式中,你有何发现?利用你的发现填空.
①__________;
②( );
③( ).
(2)利用你发现的规律来计算:.
20.(12分)阅读:我们知道,于是要解不等式,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当,即时:
解这个不等式,得:
由条件,有:
(2)当,即时,
解这个不等式,得:
由条件,有:
∴如图,综合(1)、(2)原不等式的解为
根据以上思想,请探究完成下列2个小题:
(1);
(2).
21.(12分)如图是一个运算程序:
(1)若x=﹣2,y=3,求m的值;
(2)若x=3,输出结果m的值与输入y的值相同,求y的值.
22.(13分)如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1: ;
方法2: ;
③观察图②,直接写出三个代数式(m+n)2,(m﹣n)2, mn之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若m+n=6,mn=4,求(m﹣n)2的值.
23.(14分)某公司有A,B两种型号的客车共15辆,它们的载客量、每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
型号客车 型号客车
载客量(人/辆)
租金(元/辆)
车辆数(辆)
(1)求表中a,b的值;
(2)某中学计划租用A,B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元
①求最多能租用多少辆A型客车?
②若七年级的师生共有195人,请写出所有可能的租车方案
参考答案
1.A
【解析】A、,9的平方根是,故A选项正确;
B、1的立方根是它本身1,故B选项错误;
C、,故C选项错误;
D、是5的一个平方根,故D选项错误,故选A.
2.C
【解析】无理数有:-π,,0.131131113…(每两个3之间依次多一个1),共3个.
故选C.
3.C
【解析】∵,,
∴A.,
B.,
C.,
D.,
综上所述,最小的正数是0.01,故选:C.
4.D
【解析】A、根据不等式的性质(2),不等式两边同乘以3,不等号的方向不变.故该选项成立;
B、根据不等式的性质(1),不等式两边同加上5,不等号的方向不变.故该选项成立;
C、根据不等式的性质(1)和(2),不等式的两边同乘以,再同减去1,不等号的方向不变.故该选项成立;
D、根据不等式的性质(1)和(3),不等式两边同乘以-1,则不等号的方向改变,再同加上
5.B
【解析】
解不等式①得:,
解不等式②得:,
∴不等式组的解集是,
解集在数轴上表示如图:
故选B.
6.D
【解析】A、x2、x3不是同类项,不能合并运算,故此选项错误;
B、,故此选项错误;
C、,故此选项错误;
D、,故此选项正确,故选:D.
7.A
【解析】根据不等式的基本性质1可得,选项B、D错误;
根据不等式的基本性质1,2可得,选项C错误;
根据不等式的基本性质3可得,选项A正确.故选A.
8.D
【解析】∵am=4,an=3,
∴a2m+n=(am)2×an=42×3=48.
故选:D.
9.C
【解析】, ,,
∴,故选C.
10.C
【解析】
,
由①得:x>a,
由②得:x<1,
由于不等式组无解,
所以a≥1;
解方程得
x=,
由方程的解是非负数,则有
≥0,
解得:a≤,
所以a的取值范围为1≤a≤,
所以满足条件的整数a为1、2、3,共3个,故选C.
11.2.2×10-10
【解析】0.000 000 000 22=2.2×10-10,
故答案为:2.2×10-10.
12.18或21.
【解析】根据题意得,x﹣5=0,y﹣8=0,
解得x=5,y=8,
①5是腰长时,三角形的三边分别为5、5、8,
∵5+5>8,
∴能组成三角形,周长为18;
②5是底边时,三角形的三边分别为5、8、8,
能组成三角形,
周长=8+8+5=21.
综上所述,等腰三角形的周长是18或21.
故答案为18或21.
13.20
【解析】∵某正数的两个平方根分别是a+3和2a-15,b的立方根是-2,
∴a+3+2a-15=0,b=(-2)3=8,
解得,3a=12,b=8,
∴;故答案为:20.
14.4
【解析】根据题意,将x=3,y=5代入方程得:3a﹣10=2,
解得:a=4,
故答案为:4.
15.5﹣π
【解析】原式=4﹣1﹣(π﹣3)+(﹣1)
=3﹣π+3﹣1
=5﹣π.
16.2x-3y;7.
【解析】原式=(4x2-y2-6xy+y2)÷(2x)
=(4x2-6xy) ÷(2x)
=2x-3y
当x=2,y=-1时,原式=4+3=7.
17. 解:解不等式x-3(x-2)≥4,得:x≤1,
解不等式得:x<4,
则不等式组的解集为x≤1,
将不等式组的解集表示在数轴上如下:
18.(1),,;(3)
【解析】
(1)∵的立方根是3,的算术平方根是4,
∴,,
∴,;
∵,是的整数部分,
∴;
(2)当,,时,
,16的平方根是
∴的平方根是.
19.(1)①;②;③
(2)
【解析】(1)①(x 3)(x2+3x+9)=x3 27;
②(2x+1)(4x2 2x+1)=8x3+1;
③(x y)(x2+xy+y2)=x3 y3.
故答案为①;②;③;
(2)原式
20.(1)-3≤x≤1;(2)x≥3或x≤1.
【解析】(1)|x+1|≤2,
①当x+1≥0,即x≥-1时:x+1≤2,
解这个不等式,得:x≤1
由条件x≥-1,有:-1≤x≤1;
②当x+1<0,即 x<-1时:-(x+1)≤2
解这个不等式,得:x≥-3
由条件x<-1,有:-3≤x<-1
∴综合①、②,原不等式的解为:-3≤x≤1.
(2)|x-2|≥1
①当x-2≥0,即x≥2时:x-2≥1
解这个不等式,得:x≥3
由条件x≥2,有:x≥3;
②当x-2<0,即 x<2时:-(x-2)≥1,
解这个不等式,得:x≤1,
由条件x<2,有:x≤1,
∴综合①、②,原不等式的解为:x≥3或x≤1.
21.(1)-13;(2)
【解析】(1)∵,,,
∴,
∴;
(2)∵,输出结果m的值与输入y的值相同,
∴,
①当时,
∴,
∴,
解得,符合题意;
②当时,
∴,
∴,
∴,
解得,不符合题意;
∴.
22.(1)①;②,,③;(2)20.
【解析】(1)①观察图②中的阴影部分的正方形的边长为:m﹣n.
故答案为m﹣n;
②两种不同的方法表示图②中阴影部分的面积:
方法1:;
方法2: -4mn
故答案为: 、-4mn;
③观察图②,三个代数式,,mn之间的等量关系:
=-4mn
故答案为: =-4mn;
(2)根据(1)题中的等量关系:
把m+n=6,mn=4代入: =-4mn
∴=36-16=20.
答:的值为20.
23.(1);(2)①最多能租用4辆A型客车;②所有的租车方案为:方案一:租用A种型号的客车3辆,租用B种型号的客车2辆;方案二:租用A种型号的客车4辆,租用B种型号的客车1辆
【解析】(1)由题意得:,
解得:,
即;
(2)①设计划租用A种型号客车x辆,则计划租用B种型号客车(5﹣x)辆,
根据题意得:400x+280(5﹣x)≤1900,
解得:x≤,
∵x为正整数,
∴x最大取4,
故最多能租用4辆A型客车;
②根据题意得:45x+30(5﹣x)≥195,
解得:x≥3,
∵x取正整数,
∴x=3、4,
故所有的租车方案为
方案一:租用A种型号的客车3辆,租用B种型号的客车2辆;
方案二:租用A种型号的客车4辆,租用B种型号的客车1辆.
同课章节目录
