4.2全反射同步练习 (word版含答案)
文档属性
| 名称 | 4.2全反射同步练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-11 00:00:00 | ||
图片预览




文档简介
4.2 全反射 同步练习
一、单选题
1.单镜头反光相机简称单反相机,它用一块放置在镜头与感光部件之间的透明平面镜把来自镜头的图像投射到对焦屏上。对焦屏上的图像通过五棱镜的反射进入人眼中。图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直AB射入,分别在CD和EA上发生全反射,且两次反射的入射角相等,最后光线重直BC射出。则下列说法正确的是( )
A.五棱镜的A、C两个角一定相等
B.五棱镜的E、D两个角一定相等
C.这个五棱镜的折射率最小值为
D.光线在CD边界的入射角为
2.如图是同一单色光从介质a斜射向空气时的光路图,下列说法正确的是( )
A.介质a的折射率为
B.增大入射角,光在界面不可能发生全反射
C.光在空气中的频率大于在介质a中的频率
D.光在空气中的传播速度大于在介质a中的传播速度
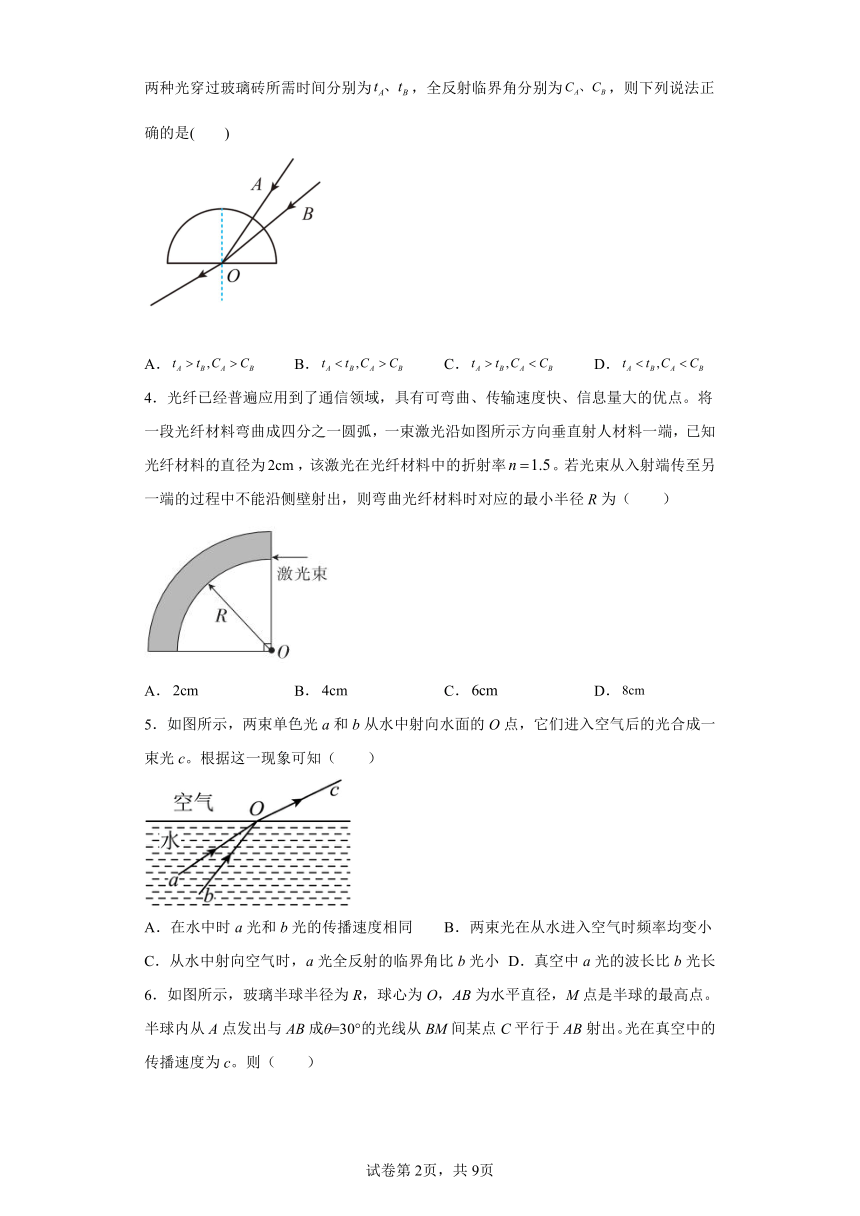
3.如图所示,某学校探究性学习小组的同学用两种颜色的激光以不同的角度同时沿不同的半径方向射入同一块半圆形玻璃砖,其折射光线由圆心O点射出后重合。两种光穿过玻璃砖所需时间分别为,全反射临界角分别为,则下列说法正确的是( )
A. B. C. D.
4.光纤已经普遍应用到了通信领域,具有可弯曲、传输速度快、信息量大的优点。将一段光纤材料弯曲成四分之一圆弧,一束激光沿如图所示方向垂直射人材料一端,已知光纤材料的直径为,该激光在光纤材料中的折射率。若光束从入射端传至另一端的过程中不能沿侧壁射出,则弯曲光纤材料时对应的最小半径R为( )
A. B. C. D.
5.如图所示,两束单色光a和b从水中射向水面的O点,它们进入空气后的光合成一束光c。根据这一现象可知( )
A.在水中时a光和b光的传播速度相同 B.两束光在从水进入空气时频率均变小
C.从水中射向空气时,a光全反射的临界角比b光小 D.真空中a光的波长比b光长
6.如图所示,玻璃半球半径为R,球心为O,AB为水平直径,M点是半球的最高点。半球内从A点发出与AB成θ=30°的光线从BM间某点C平行于AB射出。光在真空中的传播速度为c。则( )
A.此玻璃的折射率为
B.光从A到C的时间为
C.若增大θ,光线不可能在C与M间发生全反射
D.若θ为某个不为零的值,光从A到B的时间为
7.一束单色光从空气射入水中,下列说法中正确的是( )
A.光的频率不会变化 B.光的传播速度变大
C.折射角大于入射角 D.有可能发生全反射
8.半径为R、长为L的半圆柱形玻璃砖置于水平桌面上,玻璃砖的上表面水平。O为半圆形截面的圆心,一单色平行光束从半圆柱体的矩形上表面射入,该光束平行于半圆形截面并与上表面成45°,如图所示。已知该玻璃砖的折射率为,光在真空中传播速度为c,不考虑光线在玻璃砖内的多次反射,下列说法正确的是( )
A.从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
B.从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
C.该光束射入玻璃砖后,有光线射出的圆柱面的面积为
D.该光束射入玻璃砖后,有光线射出的圆柱面的面积为
9.一束单色光从介质内射入空气,其光路如图所示,下列说法中正确的是( )
A.光从介质射入空气后,光的波长变小
B.此介质的折射率等于
C.入射角大于时一定发生全反射现象
D.入射角小于时可能发生全反射现象
10.如图所示。半径为R的透明球体固定在水平地面上,其上方恰好与一足够大的水平光屏接触。O为球心,其底部S点有一点光源,透明球体对光的折射率。不考虑光在透明球体中的反射。则光屏上被光照亮区域的面积为( )
A. B. C. D.
11.某班同学在探究光发生全反射的条件,将两束光线(红光和绿光)以相同的方向由空气射入半圆形玻璃砖,半圆形玻璃对红光和绿光的折射率分别为n1,n2(n2>n1),下列哪种情况是在探究实验中可能发生的(图中O点是半圆形玻璃砖的圆心)( )
A. B.
C. D.
12.半径为R的半圆柱体玻璃砖的横截面如图所示,两束单色光垂直直径射向圆心O处。若将单色光a向上平移至距圆心处,将单色光b向下平移至距圆心处,玻璃砖右侧面恰好没有光线射出,不考虑光的多次反射。则该玻璃砖对单色光的折射率的比值为( )
A. B. C. D.2
二、填空题
13.在北方寒冷的冬天,有时会出现“多个太阳”的“幻日”奇观,这时由于空气中的水蒸气在集冷的大气里凝结成了小冰晶,太阳通过冰晶折射的缘故.如图所示为太阳光照射到六角冰晶上折射的光路图,a、b是太阳光中的两种单色光,由此可以判断,冰晶对单色光a的折射率_________(填“大于”或“小于”)冰晶对单色光b的折射率,单色光a在冰晶中的传播速度比单色光b在冰晶中的传播速度_________(填“大”或“小”).如果让太阳光从水中射向空气,逐渐增大入射角,则a、b两种单色光中,单色光_________(填“a”或“b”)更容易发生全反射.
14.观察全反射现象
如图让光沿着半圆形玻璃砖的半径射到它的平直的边上,在这个边与空气的界面上会发生反射和折射。逐渐增大入射角,观察反射光线和折射光线的变化。
实验现象
随着入射角的逐渐增大的过程中
折射角逐渐___________;
折射光线亮度逐渐___________;
反射角逐渐___________;
反射光线亮度逐渐___________;
当入射角增大到某一角度时,折射光线消失,___________。
全反射的定义
全反射:___________,___________,光线全部被反射回原光密介质的现象。
临界角:当光从光密介质射入光疏介质时,折射角等于90°角时的入射角叫做临界角。用C表示。
发生全反射的条件
(1)光从光密介质射入光疏介质;
(2)入射角等于或大于临界角;
临界角C的大小由折射率可得:___________
临界角的正弦值:___________
15.如图所示,ABCD为某棱镜的横截面,其中∠B=∠C=90°,∠D=75°,某同学想测量该棱镜的折射率,他用激光笔从BC边上的P点射入一束激光,激光从Q点射出时与AD边的夹角为45°,已知QE⊥BC,∠PQE=15°,则该棱镜的折射率为_____,若改变入射激光的方向,使激光在AD边恰好发生全反射,其反射光直接射到CD边后_____(能或不能)从CD边射出。
16.如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出。
(1)则该玻璃棒的折射率n=________;
(2)若将入射光向N端平移,当第一次射到弧面EF上时________ (填“能”“不能”或“无法确定能否”)发生全反射。
17.玻璃片形状如图示,为直角,,玻璃材料折射率为1.5,细光束从HM边垂直入射,第一次经HN边__________(填“会”或“不会”)发生全反射。光线第一次射到MN边,出射光线与法线夹角___________60°(填“大于”“等于”或“小于”)。
三、解答题
18.如图,正方体玻璃砖边长,和点分别为玻璃砖上、下表面的中点。现有一束单色光与玻璃砖上表面成角射向点。单色光经玻璃砖折射后沿着射到的中点。已知光在真空中的传播速度。求:(结果可用根式表示)
(1)玻璃砖的折射率;
(2)单色光在玻璃砖内从传播到的时间。
19.有两个半径均为R的不同透明材料制成的半圆形砖甲和乙,CD是半圆的直径,O为圆心。某单色光分别垂直射到半圆形砖甲和乙的CD表面的A点和B点,如图所示(乙图未画出)。半圆形砖甲和乙对该单色光的折射率分别为和,已知。求:该单色光分别在甲、乙中传播的时间t1和t2之比。
20.图所示,阴影部分为一均匀透明材料做成的柱形光学元件的横截面,是一半径为R的圆弧,D为圆弧的圆心,构成正方形,在D处有一单色线光源。当光从中点E射出时,折射光线的反向延长线过中点F,不考虑二次反射和折射。求:
①该材料对该光的折射率;
②当光的入射点由A点旋转到C点过程中,边有光射出的区域的长度。
21.如图所示,P、Q是两条平行的、相同的单色光线,入射到半径为R的半圆柱形玻璃砖上表面,玻璃砖下表面AB水平,在AB下方与AB相距h=R的水平光屏MN足够大,已知玻璃砖对P、Q光线的折射率均为。光线P沿半径DO方向射入,恰好在圆心O点发生全反射;光线Q从最高点E射入玻璃砖,经折射从下表面AB穿出并打在光屏MN上的F点(图中未画出)。求:
(1)临界角;
(2)O点与F点的水平距离。
22.一水池宽d=1.2m,深h=1.6m,在水池边上直立一根高H=0.8m的木杆AB,一光源D发射激光束,光源D位于水池口部F正下方0.8m处。当水池中没有水时,光源发出的光刚好照到B点。不改变光源的方向,当池内装满水时,光源发出的光照到木杆上的E点,AE=0.45m。
(1)求水的折射率;
(2)将光源移到底部的G点,当池内装满水时,改变发射激光束的方向,光束能否在水面发生全反射?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【详解】
根据题意画出光路图如图
根据光路图和反射定律可知
解得
由四边形内角和为360°和角度关系可得
由图中几何关系不能得出五棱镜的E、D两个角一定相等,光线在CD和AE界面上恰好发生全反射时,对应着五棱镜折射率的最小值n,则
解得
故A正确,BCD错误。
故选A。
2.D
【详解】
A.由图可知,介质的折射率为
故A错误;
B.由介质进入空气,增大入射角,当入射角达到临界角时,光在界面能发生全反射,故B错误;
C.光在空气中的频率等于在介质a中的频率,故C错误;
D.设光在介质a中的传播速度为,根据公式
可得
由图可知
则光在空气中的传播速度大于在介质a中的传播速度,故D正确。
故选D。
3.C
【详解】
由图知A光的折射率n更大,光在介质中的速度为
可知A光在玻璃砖中的速度比B光的小,根据
A、B光的光程一样,所以A光穿过玻璃砖所需时间较长,即
由全发射临界角公式
可知A光的全反射临界角比B光的小,即
故C正确,ABD错误。
故选C。
4.B
【详解】
当光纤材料内侧弯曲达到最小半径R时,光线恰好在材料中发生全反射,光路图如图
根据全反射条件有
根据几何关系有
联立整理代入数据可得
R=4cm
故选B。
5.D
【详解】
A.由光的可逆性可知,如果光从空气射入水中时,则a光偏折的程度较小,可知a光在水中的折射率小,由可知,在水中时a光比b光的传播速度大,A错误;
B.光的频率由光源决定,与传播的介质无关,所以两束光在从水进入空气时频率均保持不变,B错误;
C.从水中射向空气时,由可知,a光全反射的临界角比b光大,C错误;
D.a光在水中的折射率小,由折射率与光的频率关系可知,a光的频率小,由公式可知,a光的波长大, D正确。
故选D。
6.D
【详解】
A.如图所示
由几何关系可得
根据折射定律有
A错误;
B.光从A到C的时间为
联立解得
B错误;
C.若增大θ,入射角增大,由光密到光疏,当入射角大于临界角时,光线可能在C与M间发生全反射,C错误;
D.如图所示当光的入射角为时
光在M点的反射光线经过B点,光从A到B的时间为
D正确。
故选D。
7.A
【详解】
A.光的频率由光源而定,在传播过程中不会变化,故A正确;
B.因介质的折射率为
其中n为介质相对于真空的折射率且大于1, c为光在真空中的速度,v为光在介质中的速度,可知光从空气射入水中时,光的传播速度变小,故B错误;
C.因介质的折射率定义为
可知光从空气射入水中时,折射角小于入射角,故C错误;
D.发生全反射的条件之一是从光密介质到光疏介质,而相对于空气和水而言,水是光密介质,则光从空气射入水中,不可能发生全反射,故D错。
故选A。
8.D
【详解】
AB.根据折射定律得
得
根据
从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
选项AB错误;
CD.根据
得
所以临界角
因,所有折射光线与法线的夹角均为30°。对于从AO间入射的光线,某折射光线刚好在D点发生全反射,则有
所以
当∠AOD<75°时,发生全反射不能从AD间玻璃下表面射出。对于从OB间入射的光线,设折射光线刚好在C点发生全反射,此时
故能够从半圆柱球面上出射的光束范围限制在圆弧DC区域上,设其对应的圆心角为φ,则
所以玻璃砖下表面有光线射出部分的面积
选项C错误,D正确。
故选D。
9.B
【详解】
A.光从介质射到空气中,光的速度变快,但频率不变,根据
可知光的波长变长,A错误;
B.该介质的折射率
B正确;
CD.当折射角等于时,发生全反射,此时入射角为C,则有
解得
即入射角大于等于时才能发生全反射,CD错误。
故选B。
10.B
【详解】
设透明介质的临界角为C,则
解得
如图所示
光屏上光照面是以D为圆心,BD为半径的圆。光线恰好在球体内发生全反射时的入射角等于临界角C,由几何关系可得其半径
光屏上光照面积
故B正确。
故选B。
11.C
【详解】
AB.图中两束光线(红光和绿光)以相同的方向由空气射入半圆形玻璃砖,反生反射的同时会发生折射,折射角小于入射角,故AB错误;
CD.发生全反射的条件之一是光从光密介质射入光疏介质,根据
红光的临界角较大,所以当入射角大于等于红光的临界角时,两光会同时发生全反射,不可能出现红光发生全反射而绿光不发生全反射的情况,故C正确,D错误。
故选C。
12.C
【详解】
玻璃砖右侧面恰好没有光线射出,说明光在玻璃砖的右侧面均恰好发生全反射,入射角等于全反射临界角。结合几何关系,对单色光a有
由临界角公式
解得
同理,对单色光b有
解得
可知
C正确。
13. 小于 大 b
根据偏折程度可确定折射率大小关系,由可分析出光线在冰晶中传播速度的关系;根据知单色光b的临界角大小关系,从而判断更容易发生全反射的光;
【详解】
解:光从空气斜射到冰晶上,由于折射率不同,由图可知,单色b光偏折较大,单色a光偏折较小,所以此冰晶对a光的折射率小于b光的折射率;
根据可知单色光a在冰晶中的传播速度比单色光b在冰晶中的传播速度大;
根据知单色光b的临界角较小,所以单色光b比单色光a更容易发生全反射.
14. 增大 变暗 增大 变亮 光线将全部反射回光密介质中 当入射角增大到某一角度时 折射光线消失
【详解】
[1][2][3][4][5] 随着入射角的逐渐增大的过程中
折射角逐渐增大;
折射光线亮度逐渐变暗;
反射角逐渐增大;
反射光线亮度逐渐变亮;
当入射角增大到某一角度时,折射光线消失,光线将全部反射回光密介质中
[6][7] 全反射:当入射角增大到某一角度时,折射光线消失,光线全部被反射回原光密介质的现象。临界角:当光从光密介质射入光疏介质时,折射角等于90°角时的入射角叫做临界角。用C表示。
[8][9] 发生全反射的条件
(1)光从光密介质射入光疏介质;
(2)入射角等于或大于临界角;
临界角C的大小由折射率可得
临界角的正弦值
15. 激光能够从CD边出射
【详解】
[1]如图1所示,FG为法线
因,,则
根据折射定律有
[2]设全发射临界角为C,如图2所示
根据全反射条件有
解得
根据几何知识可得
因而
激光在CD边的入射角,因而激光能够从CD边出射。
16. 能
【详解】
(1)[1]发生全反射的临界角
得
(2)[2]将入射光向N端平移,由于入射角变大,在弧面EF上仍发生全反射。
17. 会
【详解】
根据题意可知
由图可知
因为
所以会发生全反射,根据几何关系及反射规律可得光线第一次射到MN边,出射光线与法线夹角
18.(1);(2)
【详解】
(1)由可知,入射角,则
所以
由
得
(2)由
得
光由O传播到M的时间
19.
【详解】
根据全反射原理
所以光线在甲砖内发生全反射的临界角
在乙砖内发生全反射的临界角
由题意可知,光线射到半圆面的入射角
所以光线在甲砖内恰好发生全反射,其光路图如图所示,根据几何关系可得,单色光在甲砖中传播的距离
速度
所以该单色光在甲砖内传播的时间
由题意可知,光射到半圆面乙的入射角
光线在乙砖内也发生全反射,光路图如图所示,根据几何关系可得,光在乙砖内传播的距离
速度
所以光在乙砖内传播的时间
所以
20.① ;②
【详解】
① 由几何关系易得折射角
入射角满足
该材料对该光的折射率为
② 该材料的全反射临界角满足
得
设光线在AB边上恰好发生全反射时的位置离A点距离为,则
得边有光射出的区域的长度
21.(1)45°;(2)
【详解】
(1)设临界角为C,由折射定律有
代入数据解得
C=45°
(2)设光线Q在E点的入射角和折射角分别为θ1和θ2,在AB面上的折射角为θ3,则
θ1=C=45°
光路如图所示
由折射定律
解得
θ2=30°
由折射定律
解得
θ3=45°
由几何关系知
且
h=R
解得O点与F点的水平距离
22.(1);(2)不会
【详解】
(1)光路图如图
由几何关系知
所以折射率为
(2)如图
当激光束照射A点时入射角最大,此时
临界角满足
由于,所以光束不会在水面发生全反射。
答案第1页,共2页
答案第1页,共2页
一、单选题
1.单镜头反光相机简称单反相机,它用一块放置在镜头与感光部件之间的透明平面镜把来自镜头的图像投射到对焦屏上。对焦屏上的图像通过五棱镜的反射进入人眼中。图为单反照相机取景器的示意图,ABCDE为五棱镜的一个截面,AB⊥BC。光线垂直AB射入,分别在CD和EA上发生全反射,且两次反射的入射角相等,最后光线重直BC射出。则下列说法正确的是( )
A.五棱镜的A、C两个角一定相等
B.五棱镜的E、D两个角一定相等
C.这个五棱镜的折射率最小值为
D.光线在CD边界的入射角为
2.如图是同一单色光从介质a斜射向空气时的光路图,下列说法正确的是( )
A.介质a的折射率为
B.增大入射角,光在界面不可能发生全反射
C.光在空气中的频率大于在介质a中的频率
D.光在空气中的传播速度大于在介质a中的传播速度
3.如图所示,某学校探究性学习小组的同学用两种颜色的激光以不同的角度同时沿不同的半径方向射入同一块半圆形玻璃砖,其折射光线由圆心O点射出后重合。两种光穿过玻璃砖所需时间分别为,全反射临界角分别为,则下列说法正确的是( )
A. B. C. D.
4.光纤已经普遍应用到了通信领域,具有可弯曲、传输速度快、信息量大的优点。将一段光纤材料弯曲成四分之一圆弧,一束激光沿如图所示方向垂直射人材料一端,已知光纤材料的直径为,该激光在光纤材料中的折射率。若光束从入射端传至另一端的过程中不能沿侧壁射出,则弯曲光纤材料时对应的最小半径R为( )
A. B. C. D.
5.如图所示,两束单色光a和b从水中射向水面的O点,它们进入空气后的光合成一束光c。根据这一现象可知( )
A.在水中时a光和b光的传播速度相同 B.两束光在从水进入空气时频率均变小
C.从水中射向空气时,a光全反射的临界角比b光小 D.真空中a光的波长比b光长
6.如图所示,玻璃半球半径为R,球心为O,AB为水平直径,M点是半球的最高点。半球内从A点发出与AB成θ=30°的光线从BM间某点C平行于AB射出。光在真空中的传播速度为c。则( )
A.此玻璃的折射率为
B.光从A到C的时间为
C.若增大θ,光线不可能在C与M间发生全反射
D.若θ为某个不为零的值,光从A到B的时间为
7.一束单色光从空气射入水中,下列说法中正确的是( )
A.光的频率不会变化 B.光的传播速度变大
C.折射角大于入射角 D.有可能发生全反射
8.半径为R、长为L的半圆柱形玻璃砖置于水平桌面上,玻璃砖的上表面水平。O为半圆形截面的圆心,一单色平行光束从半圆柱体的矩形上表面射入,该光束平行于半圆形截面并与上表面成45°,如图所示。已知该玻璃砖的折射率为,光在真空中传播速度为c,不考虑光线在玻璃砖内的多次反射,下列说法正确的是( )
A.从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
B.从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
C.该光束射入玻璃砖后,有光线射出的圆柱面的面积为
D.该光束射入玻璃砖后,有光线射出的圆柱面的面积为
9.一束单色光从介质内射入空气,其光路如图所示,下列说法中正确的是( )
A.光从介质射入空气后,光的波长变小
B.此介质的折射率等于
C.入射角大于时一定发生全反射现象
D.入射角小于时可能发生全反射现象
10.如图所示。半径为R的透明球体固定在水平地面上,其上方恰好与一足够大的水平光屏接触。O为球心,其底部S点有一点光源,透明球体对光的折射率。不考虑光在透明球体中的反射。则光屏上被光照亮区域的面积为( )
A. B. C. D.
11.某班同学在探究光发生全反射的条件,将两束光线(红光和绿光)以相同的方向由空气射入半圆形玻璃砖,半圆形玻璃对红光和绿光的折射率分别为n1,n2(n2>n1),下列哪种情况是在探究实验中可能发生的(图中O点是半圆形玻璃砖的圆心)( )
A. B.
C. D.
12.半径为R的半圆柱体玻璃砖的横截面如图所示,两束单色光垂直直径射向圆心O处。若将单色光a向上平移至距圆心处,将单色光b向下平移至距圆心处,玻璃砖右侧面恰好没有光线射出,不考虑光的多次反射。则该玻璃砖对单色光的折射率的比值为( )
A. B. C. D.2
二、填空题
13.在北方寒冷的冬天,有时会出现“多个太阳”的“幻日”奇观,这时由于空气中的水蒸气在集冷的大气里凝结成了小冰晶,太阳通过冰晶折射的缘故.如图所示为太阳光照射到六角冰晶上折射的光路图,a、b是太阳光中的两种单色光,由此可以判断,冰晶对单色光a的折射率_________(填“大于”或“小于”)冰晶对单色光b的折射率,单色光a在冰晶中的传播速度比单色光b在冰晶中的传播速度_________(填“大”或“小”).如果让太阳光从水中射向空气,逐渐增大入射角,则a、b两种单色光中,单色光_________(填“a”或“b”)更容易发生全反射.
14.观察全反射现象
如图让光沿着半圆形玻璃砖的半径射到它的平直的边上,在这个边与空气的界面上会发生反射和折射。逐渐增大入射角,观察反射光线和折射光线的变化。
实验现象
随着入射角的逐渐增大的过程中
折射角逐渐___________;
折射光线亮度逐渐___________;
反射角逐渐___________;
反射光线亮度逐渐___________;
当入射角增大到某一角度时,折射光线消失,___________。
全反射的定义
全反射:___________,___________,光线全部被反射回原光密介质的现象。
临界角:当光从光密介质射入光疏介质时,折射角等于90°角时的入射角叫做临界角。用C表示。
发生全反射的条件
(1)光从光密介质射入光疏介质;
(2)入射角等于或大于临界角;
临界角C的大小由折射率可得:___________
临界角的正弦值:___________
15.如图所示,ABCD为某棱镜的横截面,其中∠B=∠C=90°,∠D=75°,某同学想测量该棱镜的折射率,他用激光笔从BC边上的P点射入一束激光,激光从Q点射出时与AD边的夹角为45°,已知QE⊥BC,∠PQE=15°,则该棱镜的折射率为_____,若改变入射激光的方向,使激光在AD边恰好发生全反射,其反射光直接射到CD边后_____(能或不能)从CD边射出。
16.如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出。
(1)则该玻璃棒的折射率n=________;
(2)若将入射光向N端平移,当第一次射到弧面EF上时________ (填“能”“不能”或“无法确定能否”)发生全反射。
17.玻璃片形状如图示,为直角,,玻璃材料折射率为1.5,细光束从HM边垂直入射,第一次经HN边__________(填“会”或“不会”)发生全反射。光线第一次射到MN边,出射光线与法线夹角___________60°(填“大于”“等于”或“小于”)。
三、解答题
18.如图,正方体玻璃砖边长,和点分别为玻璃砖上、下表面的中点。现有一束单色光与玻璃砖上表面成角射向点。单色光经玻璃砖折射后沿着射到的中点。已知光在真空中的传播速度。求:(结果可用根式表示)
(1)玻璃砖的折射率;
(2)单色光在玻璃砖内从传播到的时间。
19.有两个半径均为R的不同透明材料制成的半圆形砖甲和乙,CD是半圆的直径,O为圆心。某单色光分别垂直射到半圆形砖甲和乙的CD表面的A点和B点,如图所示(乙图未画出)。半圆形砖甲和乙对该单色光的折射率分别为和,已知。求:该单色光分别在甲、乙中传播的时间t1和t2之比。
20.图所示,阴影部分为一均匀透明材料做成的柱形光学元件的横截面,是一半径为R的圆弧,D为圆弧的圆心,构成正方形,在D处有一单色线光源。当光从中点E射出时,折射光线的反向延长线过中点F,不考虑二次反射和折射。求:
①该材料对该光的折射率;
②当光的入射点由A点旋转到C点过程中,边有光射出的区域的长度。
21.如图所示,P、Q是两条平行的、相同的单色光线,入射到半径为R的半圆柱形玻璃砖上表面,玻璃砖下表面AB水平,在AB下方与AB相距h=R的水平光屏MN足够大,已知玻璃砖对P、Q光线的折射率均为。光线P沿半径DO方向射入,恰好在圆心O点发生全反射;光线Q从最高点E射入玻璃砖,经折射从下表面AB穿出并打在光屏MN上的F点(图中未画出)。求:
(1)临界角;
(2)O点与F点的水平距离。
22.一水池宽d=1.2m,深h=1.6m,在水池边上直立一根高H=0.8m的木杆AB,一光源D发射激光束,光源D位于水池口部F正下方0.8m处。当水池中没有水时,光源发出的光刚好照到B点。不改变光源的方向,当池内装满水时,光源发出的光照到木杆上的E点,AE=0.45m。
(1)求水的折射率;
(2)将光源移到底部的G点,当池内装满水时,改变发射激光束的方向,光束能否在水面发生全反射?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【详解】
根据题意画出光路图如图
根据光路图和反射定律可知
解得
由四边形内角和为360°和角度关系可得
由图中几何关系不能得出五棱镜的E、D两个角一定相等,光线在CD和AE界面上恰好发生全反射时,对应着五棱镜折射率的最小值n,则
解得
故A正确,BCD错误。
故选A。
2.D
【详解】
A.由图可知,介质的折射率为
故A错误;
B.由介质进入空气,增大入射角,当入射角达到临界角时,光在界面能发生全反射,故B错误;
C.光在空气中的频率等于在介质a中的频率,故C错误;
D.设光在介质a中的传播速度为,根据公式
可得
由图可知
则光在空气中的传播速度大于在介质a中的传播速度,故D正确。
故选D。
3.C
【详解】
由图知A光的折射率n更大,光在介质中的速度为
可知A光在玻璃砖中的速度比B光的小,根据
A、B光的光程一样,所以A光穿过玻璃砖所需时间较长,即
由全发射临界角公式
可知A光的全反射临界角比B光的小,即
故C正确,ABD错误。
故选C。
4.B
【详解】
当光纤材料内侧弯曲达到最小半径R时,光线恰好在材料中发生全反射,光路图如图
根据全反射条件有
根据几何关系有
联立整理代入数据可得
R=4cm
故选B。
5.D
【详解】
A.由光的可逆性可知,如果光从空气射入水中时,则a光偏折的程度较小,可知a光在水中的折射率小,由可知,在水中时a光比b光的传播速度大,A错误;
B.光的频率由光源决定,与传播的介质无关,所以两束光在从水进入空气时频率均保持不变,B错误;
C.从水中射向空气时,由可知,a光全反射的临界角比b光大,C错误;
D.a光在水中的折射率小,由折射率与光的频率关系可知,a光的频率小,由公式可知,a光的波长大, D正确。
故选D。
6.D
【详解】
A.如图所示
由几何关系可得
根据折射定律有
A错误;
B.光从A到C的时间为
联立解得
B错误;
C.若增大θ,入射角增大,由光密到光疏,当入射角大于临界角时,光线可能在C与M间发生全反射,C错误;
D.如图所示当光的入射角为时
光在M点的反射光线经过B点,光从A到B的时间为
D正确。
故选D。
7.A
【详解】
A.光的频率由光源而定,在传播过程中不会变化,故A正确;
B.因介质的折射率为
其中n为介质相对于真空的折射率且大于1, c为光在真空中的速度,v为光在介质中的速度,可知光从空气射入水中时,光的传播速度变小,故B错误;
C.因介质的折射率定义为
可知光从空气射入水中时,折射角小于入射角,故C错误;
D.发生全反射的条件之一是从光密介质到光疏介质,而相对于空气和水而言,水是光密介质,则光从空气射入水中,不可能发生全反射,故D错。
故选A。
8.D
【详解】
AB.根据折射定律得
得
根据
从O点正下方射出玻璃砖的光线在玻璃砖中传播的时间为
选项AB错误;
CD.根据
得
所以临界角
因,所有折射光线与法线的夹角均为30°。对于从AO间入射的光线,某折射光线刚好在D点发生全反射,则有
所以
当∠AOD<75°时,发生全反射不能从AD间玻璃下表面射出。对于从OB间入射的光线,设折射光线刚好在C点发生全反射,此时
故能够从半圆柱球面上出射的光束范围限制在圆弧DC区域上,设其对应的圆心角为φ,则
所以玻璃砖下表面有光线射出部分的面积
选项C错误,D正确。
故选D。
9.B
【详解】
A.光从介质射到空气中,光的速度变快,但频率不变,根据
可知光的波长变长,A错误;
B.该介质的折射率
B正确;
CD.当折射角等于时,发生全反射,此时入射角为C,则有
解得
即入射角大于等于时才能发生全反射,CD错误。
故选B。
10.B
【详解】
设透明介质的临界角为C,则
解得
如图所示
光屏上光照面是以D为圆心,BD为半径的圆。光线恰好在球体内发生全反射时的入射角等于临界角C,由几何关系可得其半径
光屏上光照面积
故B正确。
故选B。
11.C
【详解】
AB.图中两束光线(红光和绿光)以相同的方向由空气射入半圆形玻璃砖,反生反射的同时会发生折射,折射角小于入射角,故AB错误;
CD.发生全反射的条件之一是光从光密介质射入光疏介质,根据
红光的临界角较大,所以当入射角大于等于红光的临界角时,两光会同时发生全反射,不可能出现红光发生全反射而绿光不发生全反射的情况,故C正确,D错误。
故选C。
12.C
【详解】
玻璃砖右侧面恰好没有光线射出,说明光在玻璃砖的右侧面均恰好发生全反射,入射角等于全反射临界角。结合几何关系,对单色光a有
由临界角公式
解得
同理,对单色光b有
解得
可知
C正确。
13. 小于 大 b
根据偏折程度可确定折射率大小关系,由可分析出光线在冰晶中传播速度的关系;根据知单色光b的临界角大小关系,从而判断更容易发生全反射的光;
【详解】
解:光从空气斜射到冰晶上,由于折射率不同,由图可知,单色b光偏折较大,单色a光偏折较小,所以此冰晶对a光的折射率小于b光的折射率;
根据可知单色光a在冰晶中的传播速度比单色光b在冰晶中的传播速度大;
根据知单色光b的临界角较小,所以单色光b比单色光a更容易发生全反射.
14. 增大 变暗 增大 变亮 光线将全部反射回光密介质中 当入射角增大到某一角度时 折射光线消失
【详解】
[1][2][3][4][5] 随着入射角的逐渐增大的过程中
折射角逐渐增大;
折射光线亮度逐渐变暗;
反射角逐渐增大;
反射光线亮度逐渐变亮;
当入射角增大到某一角度时,折射光线消失,光线将全部反射回光密介质中
[6][7] 全反射:当入射角增大到某一角度时,折射光线消失,光线全部被反射回原光密介质的现象。临界角:当光从光密介质射入光疏介质时,折射角等于90°角时的入射角叫做临界角。用C表示。
[8][9] 发生全反射的条件
(1)光从光密介质射入光疏介质;
(2)入射角等于或大于临界角;
临界角C的大小由折射率可得
临界角的正弦值
15. 激光能够从CD边出射
【详解】
[1]如图1所示,FG为法线
因,,则
根据折射定律有
[2]设全发射临界角为C,如图2所示
根据全反射条件有
解得
根据几何知识可得
因而
激光在CD边的入射角,因而激光能够从CD边出射。
16. 能
【详解】
(1)[1]发生全反射的临界角
得
(2)[2]将入射光向N端平移,由于入射角变大,在弧面EF上仍发生全反射。
17. 会
【详解】
根据题意可知
由图可知
因为
所以会发生全反射,根据几何关系及反射规律可得光线第一次射到MN边,出射光线与法线夹角
18.(1);(2)
【详解】
(1)由可知,入射角,则
所以
由
得
(2)由
得
光由O传播到M的时间
19.
【详解】
根据全反射原理
所以光线在甲砖内发生全反射的临界角
在乙砖内发生全反射的临界角
由题意可知,光线射到半圆面的入射角
所以光线在甲砖内恰好发生全反射,其光路图如图所示,根据几何关系可得,单色光在甲砖中传播的距离
速度
所以该单色光在甲砖内传播的时间
由题意可知,光射到半圆面乙的入射角
光线在乙砖内也发生全反射,光路图如图所示,根据几何关系可得,光在乙砖内传播的距离
速度
所以光在乙砖内传播的时间
所以
20.① ;②
【详解】
① 由几何关系易得折射角
入射角满足
该材料对该光的折射率为
② 该材料的全反射临界角满足
得
设光线在AB边上恰好发生全反射时的位置离A点距离为,则
得边有光射出的区域的长度
21.(1)45°;(2)
【详解】
(1)设临界角为C,由折射定律有
代入数据解得
C=45°
(2)设光线Q在E点的入射角和折射角分别为θ1和θ2,在AB面上的折射角为θ3,则
θ1=C=45°
光路如图所示
由折射定律
解得
θ2=30°
由折射定律
解得
θ3=45°
由几何关系知
且
h=R
解得O点与F点的水平距离
22.(1);(2)不会
【详解】
(1)光路图如图
由几何关系知
所以折射率为
(2)如图
当激光束照射A点时入射角最大,此时
临界角满足
由于,所以光束不会在水面发生全反射。
答案第1页,共2页
答案第1页,共2页
