5.3导数在研究函数中的应用 同步练习(Word版含解析)
文档属性
| 名称 | 5.3导数在研究函数中的应用 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 252.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 05:29:26 | ||
图片预览

文档简介
选择性必修第二册 5.3导数在研究函数中的应用
一、单选题
1.已知函数,则不等式的解集是( )
A. B. C. D.
2.已知偶函数的定义域为,导函数为,,,则不等式的解集为( )
A.或 B.或
C.或 D.或
3.若不等式对恒成立,则实数a的取值范围是( )
A. B. C. D.
4.已知函数在,上单调递增,在上单调递减,则实数a的取值范围为( )
A. B.
C. D.
5.函数的图象大致为( )
A. B. C. D.
6.已知函数的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为( )
A. B. C. D.1
7.若点不在函数的图象上,且过点仅能作一条直线与的图象相切,则的取值范围为( )
A. B. C. D.
8.已知函数,则“”是“有极值”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
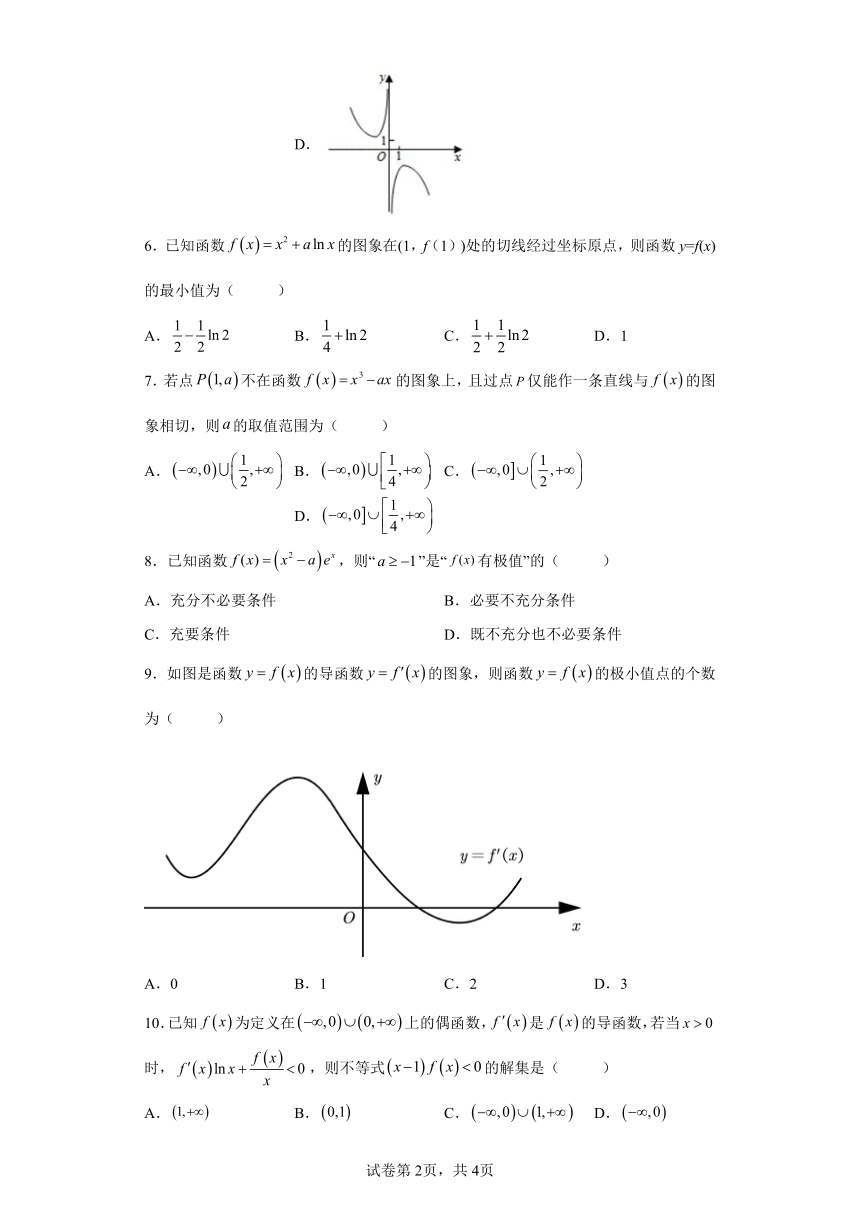
9.如图是函数的导函数的图象,则函数的极小值点的个数为( )
A.0 B.1 C.2 D.3
10.已知为定义在上的偶函数,是的导函数,若当时,,则不等式的解集是( )
A. B. C. D.
11.某莲藕种植塘每年的固定成本是2万元,每年最大规模的种植量是10万千克,每种植1万千克莲藕,成本增加1万元销售额(单位:万元)与莲藕种植量(单位:万千克)满足(为常数),若种植3万千克,销售利润是万元,则要使销售利润最大,每年需种植莲藕( )
A.6万千克 B.8万千克 C.7万千克 D.9万千克
12.已知函数在上有两个零点,则a的取值范是( )
A. B.
C. D.
13.函数的单调递增区间是( )
A. B. C. D.
14.已知定义在上的函数,其导函数为,若,且当时,,则不等式的解集为( )
A. B. C. D.
15.已知函数,若不等式的解集为,且,则函数的极大值为( )
A. B. C.0 D.
二、填空题
16.函数是R上的单调递增函数,则a的取值范围是______.
17.已知函数,则的极小值为______.
18.若函数在上为减函数,则的取值范围为___________.
三、解答题
19.已知函数.
(1)若函数的图象在点处的切线与轴垂直,求实数的值及函数在区间上的单调区间;
(2)若函数在区间上单调递增,求实数的取值范围.
20.已知函数f(x)=x3+ax2+bx+c在x=-与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对,不等式恒成立,求c的取值范围.
21.设函数,已知是函数的极值点.
(1)求a;
(2)设函数.证明:.
22.已知,.
(1)讨论的单调性;
(2)若有2个不同的零点,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.D
3.C
4.A
5.B
6.C
7.A
8.B
9.B
10.A
11.B
12.C
13.C
14.C
15.B
16.
17.
18.
19.(1),单调递增区间为,单调递减区间为
(2)
20.(1),单调递增区间为和 ,单调递减区间为;(2)或
21.(1);(2)证明见详解
22.(1)答案见解析;(2).
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知函数,则不等式的解集是( )
A. B. C. D.
2.已知偶函数的定义域为,导函数为,,,则不等式的解集为( )
A.或 B.或
C.或 D.或
3.若不等式对恒成立,则实数a的取值范围是( )
A. B. C. D.
4.已知函数在,上单调递增,在上单调递减,则实数a的取值范围为( )
A. B.
C. D.
5.函数的图象大致为( )
A. B. C. D.
6.已知函数的图象在(1,f(1))处的切线经过坐标原点,则函数y=f(x)的最小值为( )
A. B. C. D.1
7.若点不在函数的图象上,且过点仅能作一条直线与的图象相切,则的取值范围为( )
A. B. C. D.
8.已知函数,则“”是“有极值”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9.如图是函数的导函数的图象,则函数的极小值点的个数为( )
A.0 B.1 C.2 D.3
10.已知为定义在上的偶函数,是的导函数,若当时,,则不等式的解集是( )
A. B. C. D.
11.某莲藕种植塘每年的固定成本是2万元,每年最大规模的种植量是10万千克,每种植1万千克莲藕,成本增加1万元销售额(单位:万元)与莲藕种植量(单位:万千克)满足(为常数),若种植3万千克,销售利润是万元,则要使销售利润最大,每年需种植莲藕( )
A.6万千克 B.8万千克 C.7万千克 D.9万千克
12.已知函数在上有两个零点,则a的取值范是( )
A. B.
C. D.
13.函数的单调递增区间是( )
A. B. C. D.
14.已知定义在上的函数,其导函数为,若,且当时,,则不等式的解集为( )
A. B. C. D.
15.已知函数,若不等式的解集为,且,则函数的极大值为( )
A. B. C.0 D.
二、填空题
16.函数是R上的单调递增函数,则a的取值范围是______.
17.已知函数,则的极小值为______.
18.若函数在上为减函数,则的取值范围为___________.
三、解答题
19.已知函数.
(1)若函数的图象在点处的切线与轴垂直,求实数的值及函数在区间上的单调区间;
(2)若函数在区间上单调递增,求实数的取值范围.
20.已知函数f(x)=x3+ax2+bx+c在x=-与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对,不等式恒成立,求c的取值范围.
21.设函数,已知是函数的极值点.
(1)求a;
(2)设函数.证明:.
22.已知,.
(1)讨论的单调性;
(2)若有2个不同的零点,求实数的取值范围.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
2.D
3.C
4.A
5.B
6.C
7.A
8.B
9.B
10.A
11.B
12.C
13.C
14.C
15.B
16.
17.
18.
19.(1),单调递增区间为,单调递减区间为
(2)
20.(1),单调递增区间为和 ,单调递减区间为;(2)或
21.(1);(2)证明见详解
22.(1)答案见解析;(2).
答案第1页,共2页
答案第1页,共2页
