7.5正态分布 同步练习(Word版含解析)
文档属性
| 名称 | 7.5正态分布 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 692.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 05:44:19 | ||
图片预览




文档简介
7.5 正态分布 同步练习
一、单选题
1.2020年2月,受新冠肺炎的影响,医卫市场上出现了“一罩难求”的现象.在政府部门的牵头下,部分工厂转业生产口罩,已知某工厂生产口罩的质量指标,单位为g,该厂每天生产的质量在的口罩数量为818600件,则可以估计该厂每天生产的质量在15.15g以上的口罩数量为( )
参考数据:若,则,,.
A.158 700 B.22 750 C.2 700 D.1 350
2.设随机变量,若二项式,则( )
A., B.,
C., D.,
3.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
4.已知随机变量,若,则( )
A. B. C. D.
5.红外体温计的工作原理是通过人体发出的红外热辐射来测量体温的,有一定误差.用一款红外体温计测量一位体温为36.9℃的人时,显示体温X服从正态分布,若X的值在内的概率约为0.9973,则n的值约为( )
参考数据:若,则.
A.4 B.5 C.6 D.7
6.下列说法正确的个数是
①某同学投篮的命中率为0.6,他10次投篮中命中的次数是一个随机变量,且;
②某福彩中奖概率为,某人一次买了8张,中奖张数是一个随机变量,且;
③从装有5个红球、5个白球的袋中,有放回地摸球,直到摸出白球为止,则摸球次数是随机变量,且
A.0个 B.1个 C.2个 D.3个
7.在某次联考数学测试中,学生成绩服从正态分布,,若在内的概率为0.8,则落在内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
8.医用口罩由口罩面体和拉紧带组成,其中口罩面体分为内、中、外三层.内层为亲肤材质(普通卫生纱布或无纺布),中层为隔离过滤层(超细聚丙烯纤维熔喷材料层),外层为特殊材料抑菌层(无纺布或超薄聚丙烯熔喷材料层).根据国家质量监督检验标准,医用口罩的过滤率是重要的指标,根据长期生产经验,某企业在生产线状态正常情况下生产的医用口罩的过滤率.若,则,,.有如下命题:甲:;乙:;丙:;丁:假设生产状态正常,记表示一天内抽取的50只口罩中过滤率大于的数量,则.其中假命题是( )
A.甲 B.乙 C.丙 D.丁
9.近年来中国进入一个鲜花消费的增长期,某农户利用精准扶贫政策,贷款承包了一个新型温室鲜花大棚,种植销售红玫瑰和白玫瑰.若这个大棚的红玫瑰和白玫瑰的日销量分别服从正态分布和,则下列选项不正确的是( )
附:若随机变量服从正态分布,则.
A.若红玫瑰日销售量范围在的概率是,则红玫瑰日销售量的平均数约为
B.红玫瑰日销售量比白玫瑰日销售量更集中
C.白玫瑰日销售量比红玫瑰日销售量更集中
D.白玫瑰日销售量范围在的概率约为
10.某工厂有甲乙两条生产线生产同一型号的机械零件,产品的尺寸分别记为X,Y,已知X,Y均服从正态分布,,,其正态分布密度曲线如图所示,则下列结论中正确的是( )
A.甲生产线产品的稳定性高于乙生产线产品的稳定性
B.甲生产线产品的稳定性低于乙生产线产品的稳定性
C.甲生产线的产品尺寸平均值大于乙生产线的产品尺寸平均值
D.甲生产线的产品尺寸平均值小于乙生产线的产品尺寸平均值
11.正态分布,,(其中,,均大于0)所对应的密度函数图象如下图所示,则下列说法正确的是( )
A.最大,最大 B.最大,最大
C.最大,最大 D.最大,最大
12.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)=( )
A.0.158 8 B.0.158 65 C.0.158 6 D.0.158 5
13.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
14.设有一正态总体,它的正态曲线是函数f(x)的图象,且,则这个正态总体的均值与标准差分别是( )
A.10与8 B.10与2
C.8与10 D.2与10
15.设随机变量服从正态分布,若,则的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
二、填空题
16.上次月考刚好有900名学生参加考试,学生的数学成绩,且,则上次月考中数学成绩在115分以上的人数大约为__________.
17.光明中学为做到学校疫情防控常态化,切实保障学生的身体健康,组织1000名学生进行了一次“防疫知识测试”(满分100分).测试后,对学生的成绩进行统计和分析,结果如下:学生的平均成绩为,方差为.学校要对成绩不低于90分的学生进行表彰.假设学生的测试成绩X近似服从正态分布(其中近似为样本平均数近似为样本方差,则估计获表彰的学生人数为___________.(四舍五入,保留整数)参考数据:随机变量Z服从正态分布,则有,,.
18.已知某批零件的长度误差(单位:毫米)服从正态分布,从中随机取一件,其长度误差落在区间内的概率为___________.
(附:若随机变量服从正态分布,则,)
三、解答题
19.某市为提升农民年收入,更好地实现2021年扶贫的工作计划,统计了2020年50位农民的年收入并制成如下频率分布直方图:
(1)根据频率分布直方图,估计50位农民的年平均收入(单位:千元)(同组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该市农民年收入服从正态分布,其中近似为年平均收入,近似为样本方差,经计算得,利用该正态分布,求:
(ⅰ)在扶贫攻坚工作中,若使该市约有占总农民人数的84.14%的农民的年收入高于该市制定的最低年收入标准,则最低年收入大约为多少千元?
(ⅱ)为了调研“精准扶贫,不落一人”的政策要求落实情况,该市随机走访了1000位农民,若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:,随机变量服从正态分布,则,,.
20.为了提高学生身体素质,引导学生广泛发展其体育爱好,某大学每年会举办一次盛大的羽毛球比赛,其赛制如下:采用七局四胜制,比赛过程中采用两种模式:前三场采用“模式1”,后四场采用“模式2”.某位选手率先在7局中拿下4局,比赛结束.现有甲、乙两位选手进行比赛,在“模式1”中,每局甲获胜的概率为,乙获胜的概率为;在“模式2”中,每局比赛双方获胜的概率都为,每局比赛结果互相独立.
(1)求5局比赛决出胜负的概率;
(2)比赛结束时,甲乙总共进行的局数记为,求的分布列与期望.
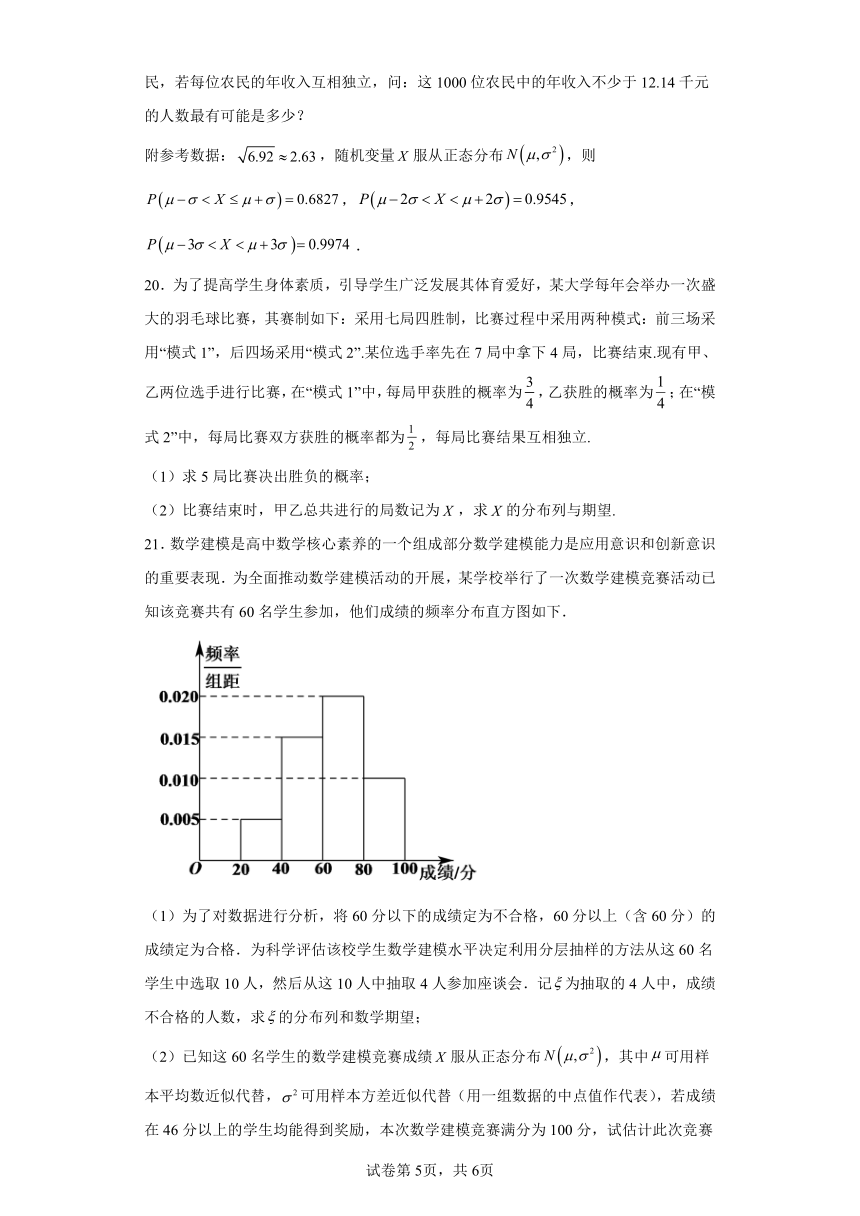
21.数学建模是高中数学核心素养的一个组成部分数学建模能力是应用意识和创新意识的重要表现.为全面推动数学建模活动的开展,某学校举行了一次数学建模竞赛活动已知该竞赛共有60名学生参加,他们成绩的频率分布直方图如下.
(1)为了对数据进行分析,将60分以下的成绩定为不合格,60分以上(含60分)的成绩定为合格.为科学评估该校学生数学建模水平决定利用分层抽样的方法从这60名学生中选取10人,然后从这10人中抽取4人参加座谈会.记为抽取的4人中,成绩不合格的人数,求的分布列和数学期望;
(2)已知这60名学生的数学建模竞赛成绩服从正态分布,其中可用样本平均数近似代替,可用样本方差近似代替(用一组数据的中点值作代表),若成绩在46分以上的学生均能得到奖励,本次数学建模竞赛满分为100分,试估计此次竞赛受到奖励的人数.(结果根据四舍五入保留到整数位)
解题中可参考使用下列数据:,,.
22.2020年我国科技成果斐然,其中北斗三号全球卫星导航系统7月31日正式开通.北斗三号全球卫星导航系统由24颗中圆地球轨道卫星、3颗地球静止轨道卫星和3颗倾斜地球同步轨道卫星,共30颗卫星组成.北斗三号全球卫星导航系统全球范围定位优于10米,实测的导航定位精度都是2~3米,全球服务可用性99%,亚太地区性能更优.
(Ⅰ)南美地区某城市通过对1000辆家用汽车进行定位测试,发现定位精确度近似满足,预估该地区某辆家用汽车导航精确度在的概率;
(Ⅱ)(ⅰ)某地基站工作人员30颗卫星中随机选取4颗卫星进行信号分析,选取的4颗卫星中含3颗倾斜地球同步轨道卫星数记为,求的分布列和数学期望;
(ⅱ)某日北京、上海、拉萨、巴黎、里约5个基地同时独立随机选取1颗卫星进行信号分析,选取的5颗卫星中含中圆地球轨道卫星的数目记为,求的数学期望.
附:若,则,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据正态分布模型,计算对应的概率值,从而求出对应的频数.
【详解】
由题意知,,即,,即;
所以,
所以该厂每天生产的口罩总量为(件),
又,
所以估计该厂每天生产的质量在15.15g以上的口罩数量为(件).
故选:D
本题主要考查了正态分布,利用正态曲线的对称性求概率,属于容易题.
2.C
利用二项式的展开式和题设条件,得到且,结合选项和二项分布的期望与方程的公式,逐项判定,即可求解.
【详解】
由题意,二项式,
因为,
可得且,
若选项A成立,则, 解得,
代入上式验证不成立,所以A错误;
若选项B成立,则, 解得,
代入上式验证不成立,所以B错误;
若选项C成立,则, 解得,
代入上式验证成立,所以C正确;
若选项D成立,则, 解得,显然不成,所以D错误.
故选:C.
3.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
4.B
利用正态密度曲线的对称性可得出,即可得解.
【详解】
因为随机变量,则.
故选:B.
5.B
根据题意求得,再结合求出,即可得出答案.
【详解】
解:因为体温X服从正态分布,
所以,
因为X的值在内的概率约为0.9973,
根据参考数据知,
即,
所以,
所以,所以,
所以,解得.
故选:B.
6.C
利用独立重复试验的概念和二项分布的定义逐一分析判断每一个命题的真假即得解.
【详解】
①某同学投篮的命中率为0.6,该同学投篮10次,是一个独立重复试验,所以他10次投篮中命中的次数是一个随机变量,且,所以该命题正确;
②某福彩中奖概率为,某人一次买了8张,相当于买了8次,每次中奖的概率都为,相当于做了8次独立重复试验,中奖张数是一个随机变量,且,所以该命题正确;
③从装有5个红球、5个白球的袋中,由于它是有放回地摸球,直到摸出白球为止,所以它不是一个独立重复性试验,因为当时,概率为,当时,概率为,当时,概率为,依次类推,即每次试验摸到白球的概率不相等,所以它不是独立重复性试验,所以不服从,所以该命题错误.
故选:C
本题主要考查独立重复试验和二项分布,意在考查学生对这些知识的理解掌握水平,属于基础题.
7.B
根据服从正态分布,得到曲线的对称轴是直线,利用在内取值的概率为0.8,即可求得结论.
【详解】
服从正态分布
曲线的对称轴是直线,
在内取值的概率为0.8,
在内取值的概率为0.5,
在内取值的概率为.
故选:.
【点评】
本题考查正态分布曲线的特点及曲线所表示的意义,主要考查正态曲线的对称性,是一个基础题.
8.D
根据正态分布曲线的特点判断A,B,C;先计算出一只口罩过滤率小于等于的概率,然后根据即可计算出的值并进行判断.
【详解】
由题意可知,正态分布的;
甲.因为,所以,故正确;
乙.因为,所以,故正确;
丙.因为,且,
所以,故正确;
丁.因为一只口罩过滤率小于等于的概率为,
又因为,故错误;
故选:D.
思路点睛:解决正态分布问题的三个关键点:
(1)对称轴;
(2)标准差;
(3)分布区间.
利用对称性可求指定范围内的概率值;由分布区间的特征进行转化,使分布区间转化为的特殊区间,从而求出所求概率.
9.C
求出的值,可判断A选项的正误;比较红玫瑰日销售量和白玫瑰日销售量方差的大小,可判断BC选项的正误;计算的值,可判断D选项的正误.
【详解】
若红玫瑰的日销售量范围在的概率是,则,解得,A对;
红玫瑰日销售量的方差为,白玫瑰日销售量的方差为,且,
故红玫瑰日销售量比白玫瑰日销售量更集中,B对C错;
因为,所以,,D对.
故选:C.
10.A
根据正态分布密度曲线的对称轴为,图像越瘦高数据越稳定可得.
【详解】
由图知甲乙两条生产线的平均值相等,甲的正态分布密度曲线较瘦高,所以甲生产线产品的稳定性高于乙生产线产品的稳定性.
故选:A
11.D
根据正态分布的均值和方差对图形的影响判断即可.
【详解】
由正态分布,可知是均值,是正态密度曲线的对称轴,可知最大,
表示方差,越小越“瘦高”,越大越“矮胖”,所以最大.
故选:D.
本题主要考查了正态分布曲线比较均值和方差,属于基础题.
12.B
根据题意可得,得出答案.
【详解】
随机变量X服从正态分布N(3,1),其图象的对称轴为X = 3.
所以
所以
故选:B
本题考查根据正态分布曲线的对称性求对应的概率,属于基础题.
13.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
14.B
结合正态密度函数的定义和解析式,即可求解.
【详解】
由正态密度函数的定义和解析式可知,总体的均值,方差,即.
故选:B.
15.B
根据正态密度曲线的对称轴得出,然后利用正态密度曲线的对称性得出可得出答案.
【详解】
随机变量服从正态分布,所以,,
,
,故选B.
本题考查正态分布的应用,意在考查正态密度曲线的对称性,属于基础题.
16.144
根据已知条件,结合正态分布的对称性,求出上次月考中数学成绩在115分以上的概率,即可求解.
【详解】
解:学生的数学成绩,,且,
,
,
则该上次月考中数学成绩在115分以上的人数大约为人.
故答案为:144.
17.23
根据正态分布概率即可求出结果.
【详解】
因为学生的平均成绩为,方差为,所以X近似服从正态分布,
所以成绩不低于90分的学生有(人).
故答案为:23.
18.0.1359
利用正态分布的对称性计算给定区间内的概率作答.
【详解】
因长度误差(单位:毫米)服从正态分布,则,
于是得,,
所以.
故答案为:0.1359
19.(1)17.40千元;(2)(ⅰ)14.77千元;(ⅱ)978人.
(1)根据平均数等于各小矩形的面积乘以矩形底边中点横坐标的和,即可求出;
(2)(ⅰ)由题意可知,,即可根据原则以及正态曲线的对称性求出;
(ⅱ)由原则以及正态曲线的对称性可知,每个农民的年收入不少于12.14千元的事件的概率为0.9773,设1000个农民的年收入不少于12.14千元的人数为,则,于是,判断的单调性求出最大值,即可解出.
【详解】
(1)
千元,故估计50位农民的年平均收入为17.40千元,
(2)由题意知
(ⅰ),所以时,
满足题意,即最低年收入大约为14.77.
(ⅱ)由,
每个农民的年收入不少于12.14千元的事件的概率为0.9773,
记1000个农民的年收入不少于12.14千元的人数为,则,其中,于是恰好有个农民的年收入不少于12.14千元的事件概率为
,从而由,得,而,所以,当时,,当时,,由此可知,在所走访的1000位农民中,年收入不少于12.14千元的人数最有可能是978人.
20.(1);(2)分布列见解析,.
(1)设在“模式1”比赛中,甲胜的场数为变量,“模式2”的比赛中甲胜的场数为变量,则令5场比赛甲胜为事件A,乙胜为事件,5场比赛之后决出胜负为事件,分别求得,从而可得出答案;
(2)写出随机变量的所有取值,求出对应随机变量的概率,从而可得出答案.
【详解】
解:(1)设在“模式1”比赛中,甲胜的场数为变量,“模式2”的比赛中甲胜的场数为变量,则令5场比赛甲胜为事件A,乙胜为事件,5场比赛之后决出胜负为事件,则:
,
,
所以
所以5场比赛决出胜负的概率为;
(2)分析值随机变量的所有可能取值为4,5,6,7,
则
所以的分布列为:
4 5 6 7
其期望为.
21.(1)分布列见解析,数学期望为;(2)50.
(1)由频率分布直方图和分层抽样的方法,可求得抽取的10人中合格的有6人,不合格的4人,则的可能值为0,1,2,3,4,然后求出对应的概率,从而可得的分布列和数学期望,
(2)由题意可求得的值,由服从正态分布和正态分布的性质可求得答案
【详解】
(1)由频率分布直方图和分层抽样的方法,可知抽取的10人中合格的人数为,不合格的人数为.因此,的可能值为0,1,2,3,4,则
,,,,.
故的分布列为
0 1 2 3 4
所以的数学期望.
(2)由题意可知,.
,所以.
由服从正态分布,得
,
则,,.
所以此次竞赛受到奖励的人数为50.
22.(Ⅰ)0.84;(Ⅱ)(ⅰ)分布列见解析,;(ⅱ)4.
(Ⅰ)根据“”原则及图形的对称性即可求解;
(Ⅱ)(ⅰ)由题可知服从超几何分布,利用公式即可求解;(ⅱ)由题可知服从二项分布,利用公式即可求解.
【详解】
(Ⅰ)由,易知
,
则预估该地区某辆家用汽车导航精确度在的概率为0.84.
(Ⅱ)(ⅰ)由题意知,,
∴的分布列为
∴.
(ⅱ)5个基地相互独立,每个基地随机选取1颗卫星是中圆地球轨道卫星的概率为,所以5个基地选取的5颗卫星中含中圆地球轨道卫星的数目,
∴.
方法点睛:本题以北斗三号全球卫星导航系统为背景,考查正态分布、超几何分布、二项分布,求离散型随机变量的分布列,首先要根据具体情况确定的取值情况,然后利用排列,组合,概率知识求出取各个值时对应的概率,对应服从某种特殊分布的随机变量,其分布列可以直接应用公式给出,考查学生逻辑推理能力与计算能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.2020年2月,受新冠肺炎的影响,医卫市场上出现了“一罩难求”的现象.在政府部门的牵头下,部分工厂转业生产口罩,已知某工厂生产口罩的质量指标,单位为g,该厂每天生产的质量在的口罩数量为818600件,则可以估计该厂每天生产的质量在15.15g以上的口罩数量为( )
参考数据:若,则,,.
A.158 700 B.22 750 C.2 700 D.1 350
2.设随机变量,若二项式,则( )
A., B.,
C., D.,
3.已知随机变量X,Y满足,且,则( )
A.2.4 B.3.4 C.4.2 D.4.4
4.已知随机变量,若,则( )
A. B. C. D.
5.红外体温计的工作原理是通过人体发出的红外热辐射来测量体温的,有一定误差.用一款红外体温计测量一位体温为36.9℃的人时,显示体温X服从正态分布,若X的值在内的概率约为0.9973,则n的值约为( )
参考数据:若,则.
A.4 B.5 C.6 D.7
6.下列说法正确的个数是
①某同学投篮的命中率为0.6,他10次投篮中命中的次数是一个随机变量,且;
②某福彩中奖概率为,某人一次买了8张,中奖张数是一个随机变量,且;
③从装有5个红球、5个白球的袋中,有放回地摸球,直到摸出白球为止,则摸球次数是随机变量,且
A.0个 B.1个 C.2个 D.3个
7.在某次联考数学测试中,学生成绩服从正态分布,,若在内的概率为0.8,则落在内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
8.医用口罩由口罩面体和拉紧带组成,其中口罩面体分为内、中、外三层.内层为亲肤材质(普通卫生纱布或无纺布),中层为隔离过滤层(超细聚丙烯纤维熔喷材料层),外层为特殊材料抑菌层(无纺布或超薄聚丙烯熔喷材料层).根据国家质量监督检验标准,医用口罩的过滤率是重要的指标,根据长期生产经验,某企业在生产线状态正常情况下生产的医用口罩的过滤率.若,则,,.有如下命题:甲:;乙:;丙:;丁:假设生产状态正常,记表示一天内抽取的50只口罩中过滤率大于的数量,则.其中假命题是( )
A.甲 B.乙 C.丙 D.丁
9.近年来中国进入一个鲜花消费的增长期,某农户利用精准扶贫政策,贷款承包了一个新型温室鲜花大棚,种植销售红玫瑰和白玫瑰.若这个大棚的红玫瑰和白玫瑰的日销量分别服从正态分布和,则下列选项不正确的是( )
附:若随机变量服从正态分布,则.
A.若红玫瑰日销售量范围在的概率是,则红玫瑰日销售量的平均数约为
B.红玫瑰日销售量比白玫瑰日销售量更集中
C.白玫瑰日销售量比红玫瑰日销售量更集中
D.白玫瑰日销售量范围在的概率约为
10.某工厂有甲乙两条生产线生产同一型号的机械零件,产品的尺寸分别记为X,Y,已知X,Y均服从正态分布,,,其正态分布密度曲线如图所示,则下列结论中正确的是( )
A.甲生产线产品的稳定性高于乙生产线产品的稳定性
B.甲生产线产品的稳定性低于乙生产线产品的稳定性
C.甲生产线的产品尺寸平均值大于乙生产线的产品尺寸平均值
D.甲生产线的产品尺寸平均值小于乙生产线的产品尺寸平均值
11.正态分布,,(其中,,均大于0)所对应的密度函数图象如下图所示,则下列说法正确的是( )
A.最大,最大 B.最大,最大
C.最大,最大 D.最大,最大
12.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.682 7,则P(X>4)=( )
A.0.158 8 B.0.158 65 C.0.158 6 D.0.158 5
13.设随机变量ξ服从正态分布N(μ,σ2),ξ<1的概率是,则μ等于( )
A.1 B.2 C.4 D.不确定
14.设有一正态总体,它的正态曲线是函数f(x)的图象,且,则这个正态总体的均值与标准差分别是( )
A.10与8 B.10与2
C.8与10 D.2与10
15.设随机变量服从正态分布,若,则的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
二、填空题
16.上次月考刚好有900名学生参加考试,学生的数学成绩,且,则上次月考中数学成绩在115分以上的人数大约为__________.
17.光明中学为做到学校疫情防控常态化,切实保障学生的身体健康,组织1000名学生进行了一次“防疫知识测试”(满分100分).测试后,对学生的成绩进行统计和分析,结果如下:学生的平均成绩为,方差为.学校要对成绩不低于90分的学生进行表彰.假设学生的测试成绩X近似服从正态分布(其中近似为样本平均数近似为样本方差,则估计获表彰的学生人数为___________.(四舍五入,保留整数)参考数据:随机变量Z服从正态分布,则有,,.
18.已知某批零件的长度误差(单位:毫米)服从正态分布,从中随机取一件,其长度误差落在区间内的概率为___________.
(附:若随机变量服从正态分布,则,)
三、解答题
19.某市为提升农民年收入,更好地实现2021年扶贫的工作计划,统计了2020年50位农民的年收入并制成如下频率分布直方图:
(1)根据频率分布直方图,估计50位农民的年平均收入(单位:千元)(同组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该市农民年收入服从正态分布,其中近似为年平均收入,近似为样本方差,经计算得,利用该正态分布,求:
(ⅰ)在扶贫攻坚工作中,若使该市约有占总农民人数的84.14%的农民的年收入高于该市制定的最低年收入标准,则最低年收入大约为多少千元?
(ⅱ)为了调研“精准扶贫,不落一人”的政策要求落实情况,该市随机走访了1000位农民,若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:,随机变量服从正态分布,则,,.
20.为了提高学生身体素质,引导学生广泛发展其体育爱好,某大学每年会举办一次盛大的羽毛球比赛,其赛制如下:采用七局四胜制,比赛过程中采用两种模式:前三场采用“模式1”,后四场采用“模式2”.某位选手率先在7局中拿下4局,比赛结束.现有甲、乙两位选手进行比赛,在“模式1”中,每局甲获胜的概率为,乙获胜的概率为;在“模式2”中,每局比赛双方获胜的概率都为,每局比赛结果互相独立.
(1)求5局比赛决出胜负的概率;
(2)比赛结束时,甲乙总共进行的局数记为,求的分布列与期望.
21.数学建模是高中数学核心素养的一个组成部分数学建模能力是应用意识和创新意识的重要表现.为全面推动数学建模活动的开展,某学校举行了一次数学建模竞赛活动已知该竞赛共有60名学生参加,他们成绩的频率分布直方图如下.
(1)为了对数据进行分析,将60分以下的成绩定为不合格,60分以上(含60分)的成绩定为合格.为科学评估该校学生数学建模水平决定利用分层抽样的方法从这60名学生中选取10人,然后从这10人中抽取4人参加座谈会.记为抽取的4人中,成绩不合格的人数,求的分布列和数学期望;
(2)已知这60名学生的数学建模竞赛成绩服从正态分布,其中可用样本平均数近似代替,可用样本方差近似代替(用一组数据的中点值作代表),若成绩在46分以上的学生均能得到奖励,本次数学建模竞赛满分为100分,试估计此次竞赛受到奖励的人数.(结果根据四舍五入保留到整数位)
解题中可参考使用下列数据:,,.
22.2020年我国科技成果斐然,其中北斗三号全球卫星导航系统7月31日正式开通.北斗三号全球卫星导航系统由24颗中圆地球轨道卫星、3颗地球静止轨道卫星和3颗倾斜地球同步轨道卫星,共30颗卫星组成.北斗三号全球卫星导航系统全球范围定位优于10米,实测的导航定位精度都是2~3米,全球服务可用性99%,亚太地区性能更优.
(Ⅰ)南美地区某城市通过对1000辆家用汽车进行定位测试,发现定位精确度近似满足,预估该地区某辆家用汽车导航精确度在的概率;
(Ⅱ)(ⅰ)某地基站工作人员30颗卫星中随机选取4颗卫星进行信号分析,选取的4颗卫星中含3颗倾斜地球同步轨道卫星数记为,求的分布列和数学期望;
(ⅱ)某日北京、上海、拉萨、巴黎、里约5个基地同时独立随机选取1颗卫星进行信号分析,选取的5颗卫星中含中圆地球轨道卫星的数目记为,求的数学期望.
附:若,则,,.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据正态分布模型,计算对应的概率值,从而求出对应的频数.
【详解】
由题意知,,即,,即;
所以,
所以该厂每天生产的口罩总量为(件),
又,
所以估计该厂每天生产的质量在15.15g以上的口罩数量为(件).
故选:D
本题主要考查了正态分布,利用正态曲线的对称性求概率,属于容易题.
2.C
利用二项式的展开式和题设条件,得到且,结合选项和二项分布的期望与方程的公式,逐项判定,即可求解.
【详解】
由题意,二项式,
因为,
可得且,
若选项A成立,则, 解得,
代入上式验证不成立,所以A错误;
若选项B成立,则, 解得,
代入上式验证不成立,所以B错误;
若选项C成立,则, 解得,
代入上式验证成立,所以C正确;
若选项D成立,则, 解得,显然不成,所以D错误.
故选:C.
3.D
根据二项分布的知识求得,然后求得,从而求得正确答案.
【详解】
由题意,知随机变量X服从二项分布,,,
则,方差,又∵,∴,
∴,
∴.
故选:D
4.B
利用正态密度曲线的对称性可得出,即可得解.
【详解】
因为随机变量,则.
故选:B.
5.B
根据题意求得,再结合求出,即可得出答案.
【详解】
解:因为体温X服从正态分布,
所以,
因为X的值在内的概率约为0.9973,
根据参考数据知,
即,
所以,
所以,所以,
所以,解得.
故选:B.
6.C
利用独立重复试验的概念和二项分布的定义逐一分析判断每一个命题的真假即得解.
【详解】
①某同学投篮的命中率为0.6,该同学投篮10次,是一个独立重复试验,所以他10次投篮中命中的次数是一个随机变量,且,所以该命题正确;
②某福彩中奖概率为,某人一次买了8张,相当于买了8次,每次中奖的概率都为,相当于做了8次独立重复试验,中奖张数是一个随机变量,且,所以该命题正确;
③从装有5个红球、5个白球的袋中,由于它是有放回地摸球,直到摸出白球为止,所以它不是一个独立重复性试验,因为当时,概率为,当时,概率为,当时,概率为,依次类推,即每次试验摸到白球的概率不相等,所以它不是独立重复性试验,所以不服从,所以该命题错误.
故选:C
本题主要考查独立重复试验和二项分布,意在考查学生对这些知识的理解掌握水平,属于基础题.
7.B
根据服从正态分布,得到曲线的对称轴是直线,利用在内取值的概率为0.8,即可求得结论.
【详解】
服从正态分布
曲线的对称轴是直线,
在内取值的概率为0.8,
在内取值的概率为0.5,
在内取值的概率为.
故选:.
【点评】
本题考查正态分布曲线的特点及曲线所表示的意义,主要考查正态曲线的对称性,是一个基础题.
8.D
根据正态分布曲线的特点判断A,B,C;先计算出一只口罩过滤率小于等于的概率,然后根据即可计算出的值并进行判断.
【详解】
由题意可知,正态分布的;
甲.因为,所以,故正确;
乙.因为,所以,故正确;
丙.因为,且,
所以,故正确;
丁.因为一只口罩过滤率小于等于的概率为,
又因为,故错误;
故选:D.
思路点睛:解决正态分布问题的三个关键点:
(1)对称轴;
(2)标准差;
(3)分布区间.
利用对称性可求指定范围内的概率值;由分布区间的特征进行转化,使分布区间转化为的特殊区间,从而求出所求概率.
9.C
求出的值,可判断A选项的正误;比较红玫瑰日销售量和白玫瑰日销售量方差的大小,可判断BC选项的正误;计算的值,可判断D选项的正误.
【详解】
若红玫瑰的日销售量范围在的概率是,则,解得,A对;
红玫瑰日销售量的方差为,白玫瑰日销售量的方差为,且,
故红玫瑰日销售量比白玫瑰日销售量更集中,B对C错;
因为,所以,,D对.
故选:C.
10.A
根据正态分布密度曲线的对称轴为,图像越瘦高数据越稳定可得.
【详解】
由图知甲乙两条生产线的平均值相等,甲的正态分布密度曲线较瘦高,所以甲生产线产品的稳定性高于乙生产线产品的稳定性.
故选:A
11.D
根据正态分布的均值和方差对图形的影响判断即可.
【详解】
由正态分布,可知是均值,是正态密度曲线的对称轴,可知最大,
表示方差,越小越“瘦高”,越大越“矮胖”,所以最大.
故选:D.
本题主要考查了正态分布曲线比较均值和方差,属于基础题.
12.B
根据题意可得,得出答案.
【详解】
随机变量X服从正态分布N(3,1),其图象的对称轴为X = 3.
所以
所以
故选:B
本题考查根据正态分布曲线的对称性求对应的概率,属于基础题.
13.A
利用正态分布图象的对称性,确定对称轴,即可知均值μ.
【详解】
由题意,ξ < 1的概率是,则ξ > 1的概率也是,
∴正态分布的图象关于对称,即.
故选:A
14.B
结合正态密度函数的定义和解析式,即可求解.
【详解】
由正态密度函数的定义和解析式可知,总体的均值,方差,即.
故选:B.
15.B
根据正态密度曲线的对称轴得出,然后利用正态密度曲线的对称性得出可得出答案.
【详解】
随机变量服从正态分布,所以,,
,
,故选B.
本题考查正态分布的应用,意在考查正态密度曲线的对称性,属于基础题.
16.144
根据已知条件,结合正态分布的对称性,求出上次月考中数学成绩在115分以上的概率,即可求解.
【详解】
解:学生的数学成绩,,且,
,
,
则该上次月考中数学成绩在115分以上的人数大约为人.
故答案为:144.
17.23
根据正态分布概率即可求出结果.
【详解】
因为学生的平均成绩为,方差为,所以X近似服从正态分布,
所以成绩不低于90分的学生有(人).
故答案为:23.
18.0.1359
利用正态分布的对称性计算给定区间内的概率作答.
【详解】
因长度误差(单位:毫米)服从正态分布,则,
于是得,,
所以.
故答案为:0.1359
19.(1)17.40千元;(2)(ⅰ)14.77千元;(ⅱ)978人.
(1)根据平均数等于各小矩形的面积乘以矩形底边中点横坐标的和,即可求出;
(2)(ⅰ)由题意可知,,即可根据原则以及正态曲线的对称性求出;
(ⅱ)由原则以及正态曲线的对称性可知,每个农民的年收入不少于12.14千元的事件的概率为0.9773,设1000个农民的年收入不少于12.14千元的人数为,则,于是,判断的单调性求出最大值,即可解出.
【详解】
(1)
千元,故估计50位农民的年平均收入为17.40千元,
(2)由题意知
(ⅰ),所以时,
满足题意,即最低年收入大约为14.77.
(ⅱ)由,
每个农民的年收入不少于12.14千元的事件的概率为0.9773,
记1000个农民的年收入不少于12.14千元的人数为,则,其中,于是恰好有个农民的年收入不少于12.14千元的事件概率为
,从而由,得,而,所以,当时,,当时,,由此可知,在所走访的1000位农民中,年收入不少于12.14千元的人数最有可能是978人.
20.(1);(2)分布列见解析,.
(1)设在“模式1”比赛中,甲胜的场数为变量,“模式2”的比赛中甲胜的场数为变量,则令5场比赛甲胜为事件A,乙胜为事件,5场比赛之后决出胜负为事件,分别求得,从而可得出答案;
(2)写出随机变量的所有取值,求出对应随机变量的概率,从而可得出答案.
【详解】
解:(1)设在“模式1”比赛中,甲胜的场数为变量,“模式2”的比赛中甲胜的场数为变量,则令5场比赛甲胜为事件A,乙胜为事件,5场比赛之后决出胜负为事件,则:
,
,
所以
所以5场比赛决出胜负的概率为;
(2)分析值随机变量的所有可能取值为4,5,6,7,
则
所以的分布列为:
4 5 6 7
其期望为.
21.(1)分布列见解析,数学期望为;(2)50.
(1)由频率分布直方图和分层抽样的方法,可求得抽取的10人中合格的有6人,不合格的4人,则的可能值为0,1,2,3,4,然后求出对应的概率,从而可得的分布列和数学期望,
(2)由题意可求得的值,由服从正态分布和正态分布的性质可求得答案
【详解】
(1)由频率分布直方图和分层抽样的方法,可知抽取的10人中合格的人数为,不合格的人数为.因此,的可能值为0,1,2,3,4,则
,,,,.
故的分布列为
0 1 2 3 4
所以的数学期望.
(2)由题意可知,.
,所以.
由服从正态分布,得
,
则,,.
所以此次竞赛受到奖励的人数为50.
22.(Ⅰ)0.84;(Ⅱ)(ⅰ)分布列见解析,;(ⅱ)4.
(Ⅰ)根据“”原则及图形的对称性即可求解;
(Ⅱ)(ⅰ)由题可知服从超几何分布,利用公式即可求解;(ⅱ)由题可知服从二项分布,利用公式即可求解.
【详解】
(Ⅰ)由,易知
,
则预估该地区某辆家用汽车导航精确度在的概率为0.84.
(Ⅱ)(ⅰ)由题意知,,
∴的分布列为
∴.
(ⅱ)5个基地相互独立,每个基地随机选取1颗卫星是中圆地球轨道卫星的概率为,所以5个基地选取的5颗卫星中含中圆地球轨道卫星的数目,
∴.
方法点睛:本题以北斗三号全球卫星导航系统为背景,考查正态分布、超几何分布、二项分布,求离散型随机变量的分布列,首先要根据具体情况确定的取值情况,然后利用排列,组合,概率知识求出取各个值时对应的概率,对应服从某种特殊分布的随机变量,其分布列可以直接应用公式给出,考查学生逻辑推理能力与计算能力,属于中档题.
答案第1页,共2页
答案第1页,共2页
