北师大版数学九年级下册 第三章 圆 8 圆内接正多边形 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 第三章 圆 8 圆内接正多边形 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 271.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 10:22:00 | ||
图片预览





文档简介
(共16张PPT)
第三章
圆
8 圆内接正多边形
正多边形:
各边相等,各角也相等的多边形叫作正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫作正n边形.
三条边相等,三个角也相等(60°).
四条边都相等,四个角也相等(90°).
知识回顾
说说图中的有哪几种正多边形
怎样解答
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
情境引入
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
—多边形是正多边形
A
B
C
D
自主预习
⌒
⌒
⌒
1
2
3
A
B
C
D
E
证明:∵AB=BC=CD=DE=EA,
∴AB=BC=CD=DE=EA.
∵BCE=CDA=3AB,
∴∠1=∠2.
同理,∠2=∠3=∠4=∠5.
又∵顶点A,B,C,D,E都在⊙O上,
∴五边形ABCDE是⊙O的内接五边形.
4
⌒
⌒
5
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
新知探究
E
F
C
D
.
.
O
中心角
半径R
边心距r
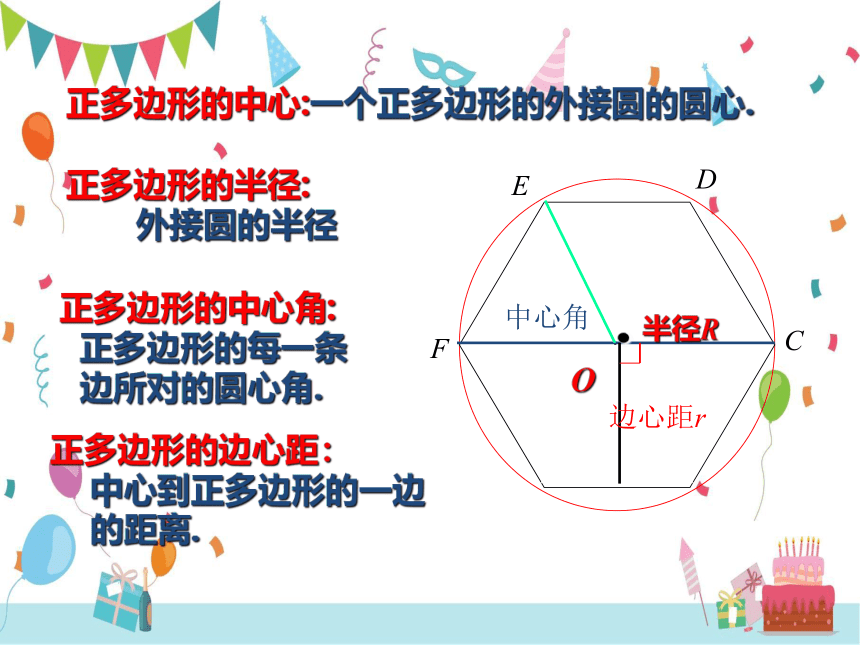
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边
的距离.
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
例 有一个亭子它的地基是半径为4 m的正六边形,求
地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
O
B
C
R
P
解:
∴亭子的周长 L=6×4=24(m).
正n边形的一个内角的度数是______________;
中心角是___________;
正多边形的中心角与外角的大小关系
是________.
相等
画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
(1)正四、正八边形的尺规作图
(2)正六、正三 、正十二边形的尺规作图
1.正方形ABCD的外接圆圆心O叫作
正方形ABCD的 .
2.正方形ABCD的内切圆的半径OE叫作正方形ABCD的
.
A
B
C
D
.O
E
中心
边心距
随堂练习
3.⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径.
4. ∠AOB叫作正五边形ABCDE的 角,它的度数是 .
D
E
A
B
C
.O
F
边心距
内切
中心
72°
5.图中正六边形ABCDEF的中心角是 ,
它的度数是 .
6.你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
7.按照一定比例,画一个停车
让行的交通标志的外缘.
停
本节课我们学习了正多边形和圆的关系.并学习正多边形的半径、边心距、中心角等定义.学会画正多边形,并会进行正多边形的有关计算.
课堂小结
第三章
圆
8 圆内接正多边形
正多边形:
各边相等,各角也相等的多边形叫作正多边形.
正n边形:如果一个正多边形有n条边,那么这个正多边形叫作正n边形.
三条边相等,三个角也相等(60°).
四条边都相等,四个角也相等(90°).
知识回顾
说说图中的有哪几种正多边形
怎样解答
想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么?
情境引入
弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等)
—多边形是正多边形
A
B
C
D
自主预习
⌒
⌒
⌒
1
2
3
A
B
C
D
E
证明:∵AB=BC=CD=DE=EA,
∴AB=BC=CD=DE=EA.
∵BCE=CDA=3AB,
∴∠1=∠2.
同理,∠2=∠3=∠4=∠5.
又∵顶点A,B,C,D,E都在⊙O上,
∴五边形ABCDE是⊙O的内接五边形.
4
⌒
⌒
5
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
新知探究
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边
的距离.
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
例 有一个亭子它的地基是半径为4 m的正六边形,求
地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
O
B
C
R
P
解:
∴亭子的周长 L=6×4=24(m).
正n边形的一个内角的度数是______________;
中心角是___________;
正多边形的中心角与外角的大小关系
是________.
相等
画正多边形的方法
1.用量角器等分圆
2.尺规作图等分圆
(1)正四、正八边形的尺规作图
(2)正六、正三 、正十二边形的尺规作图
1.正方形ABCD的外接圆圆心O叫作
正方形ABCD的 .
2.正方形ABCD的内切圆的半径OE叫作正方形ABCD的
.
A
B
C
D
.O
E
中心
边心距
随堂练习
3.⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径.
4. ∠AOB叫作正五边形ABCDE的 角,它的度数是 .
D
E
A
B
C
.O
F
边心距
内切
中心
72°
5.图中正六边形ABCDEF的中心角是 ,
它的度数是 .
6.你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
B
A
E
F
C
D
.O
∠AOB
60°
7.按照一定比例,画一个停车
让行的交通标志的外缘.
停
本节课我们学习了正多边形和圆的关系.并学习正多边形的半径、边心距、中心角等定义.学会画正多边形,并会进行正多边形的有关计算.
课堂小结
