2.5有理数加法

课件21张PPT。有理数的加法教学目标
1．使学生掌握有理数加法法则，并能运用法则进行计算；
2．在有理数加法法则的教学过程中，注意培养学生的观察、比较、归纳及运算能力．?
教学重点和难点
重点：有理数加法法则．
难点：异号两数相加的法则．某市组织一次少年足球赛，巴西队、美国队、意大利队、中国队的成绩如下：巴西队第一场比赛赢2个球，第二场比赛赢1个球，美国队第一场比赛输2个球，第二场比赛输3个球，意大利队第一场比赛赢1个球，第二场比赛输2个球，中国队第一场输1个球，第二场赢4个球。请同学们计算一下各队在这两场比赛的净胜球数。 各队在这两场比赛的净胜球数。
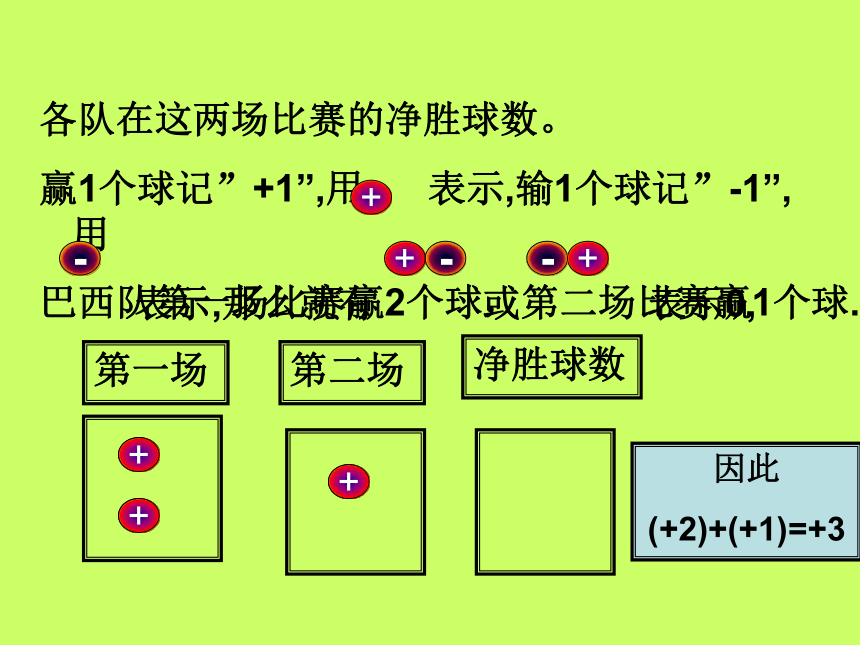
赢1个球记”+1”,用 表示,输1个球记”-1”,用
表示,那么就有 或 表示0,+-巴西队第一场比赛赢2个球，第二场比赛赢1个球.第一场第二场净胜球数++++++因此
(+2)+(+1)=+3各队在这两场比赛的净胜球数。
赢1个球记”+1”,用 表示,输1个球记”-1”,用
表示,那么就有 或 表示0,+-美国队第一场比赛输2个球，第二场比赛输3个球.第一场第二场净胜球数因此
(-2)+(-3)=-5----------+各队在这两场比赛的净胜球数。
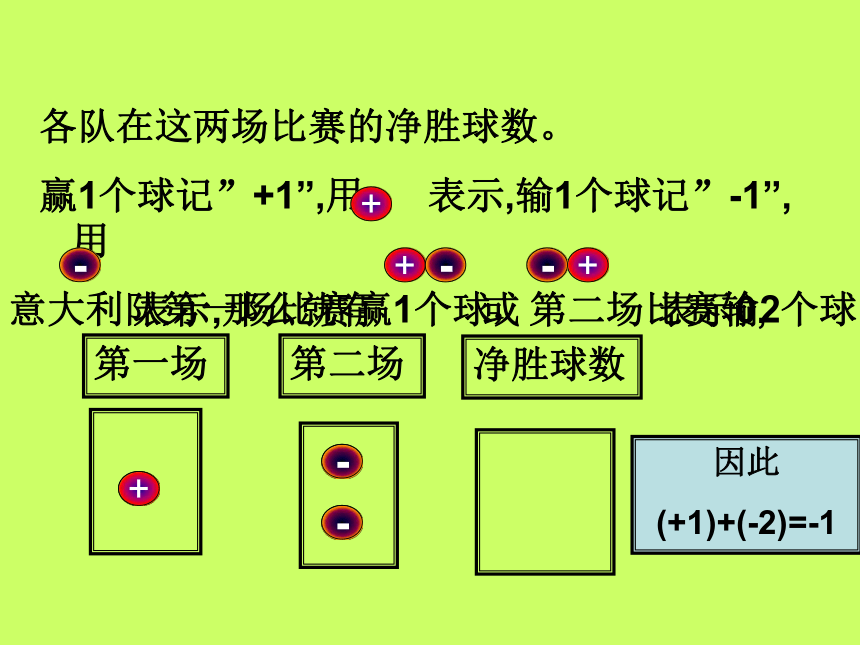
赢1个球记”+1”,用 表示,输1个球记”-1”,用
表示,那么就有 或 表示0,+-意大利队第一场比赛赢1个球，第二场比赛输2个球.第一场第二场净胜球数+因此
(+1)+(-2)=-1----各队在这两场比赛的净胜球数。
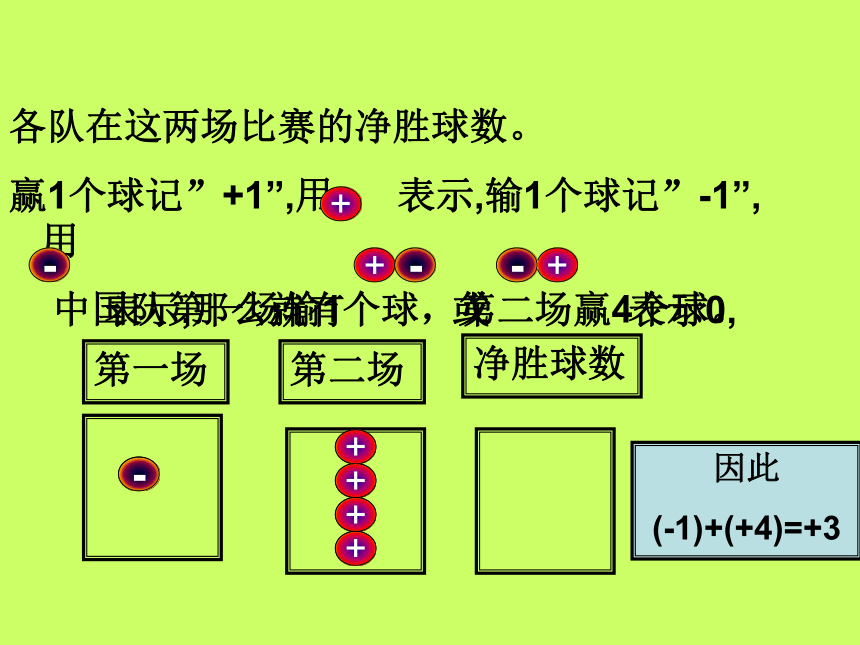
赢1个球记”+1”,用 表示,输1个球记”-1”,用
表示,那么就有 或 表示0,+-中国队第一场输1个球，第二场赢4个球。第一场第二场净胜球数+++因此
(-1)+(+4)=+3+++++---1 0 1 2 3 4 5 6 7 8(+5)+(+3)=8 5 3＋8用数轴表示加法运算1、向东走5米，再向东走3米，两次一共向东走了多少米？ -8 -7 -6 -5 -4 -3 -2 -1 0 1 - 3 - 5（-5）+（-3）=-8＋-82、向西走5米，再向西走3米， 两次一共向东走了多少米？
用数轴表示加法运算3、 向东走5米，再向西走3米， 两次一共向东走了多少米？
5+（-3）=2 -1 0 1 2 3 4 5 65-3＋2用数轴表示加法运算4、 向东走3米，再向西走5米，两次一共向东走了多少米 ？3+（-5）=-2-3 -2 -1 0 1 2 3 4 3 -5＋-2用数轴表示加法运算 5、向东走5米，再向西走5米，两次一共向东走了多少米？ 5+（-5）=0 -1 0 1 2 3 4 5 6 - 5 5＋用数轴表示加法运算6、向西走5米，再向东走0米，两次一共向东走了多少米？
（-5）+ 0 = -5 -5 -4 -3 -2 -1 0 1-5+0用数轴表示加法运算由此可见，两个有理数相加，加数可以是正数，也可以是负数；相加的结果，可以是正数，也可以是负数，所以求两个有理数的和，就可以归结为：
①确定和的符号；②确定和的绝对值.
2.有理数加法法则
(1)同号两数相加，取相同的符号，并把绝对值相加.
(2)绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值，互为相反两个数相加得0.
(3)一个数同0相加，仍得这个数.理解有理数加法法则要注意三点：
第一，法则的叙述，强调先确定和的符号，后计算和的绝对值，具体计算时要遵循这一原则;
第二，法则中异号两数相加是难点，其中“并用较大的绝对值减去较小的绝对值”不能说成是“并用较大的加数减去较小加数的绝对值”；
第三，相反数相加得0，说明正数和负数相加时，可以互相抵消或一部分被抵消，同时也说明两个数相加的和，可能小于其中的一个加数，这在小学数学认识中是不可思议的. 应用举例? 变式练习(口答)
例1? 计算下列算式的结果，并说明理由：
(1)(+4)+(+7)；???? (2)(-4)+(-7)
(3)(+4)+(-7)；?????? (4)(+9)+(-4)；
(5)(+4)+(-4)；????? (6)(+9)+(-2)；??????
(7)(-9)+(+2)；?????? (8)(-9)+0；
(9)0+(+2)；???????? (10)0+0．
进行计算时，应该先确定“和”的符号，计算“和”的绝对值． 全班学生书面练习，四位学生板演，教师对学生板演进行讲评．
(1)(-0.9)+(+1.5)；???
(2)(+2.7)+(-3)；??
(3)(-1.1)+(-2.9)；例1 计算：例2*．用“＞”或“＜”号填空：
(1)如果a＞0，b＞0，那么a+b ______0；
(2)如果a＜0，b＜0，那么a+b ______0；
(3)如果a＞0，b＜0，|a|＞|b|，那么a+b____0；
(4)如果a＜0，b＞0，|a|＞|b|，那么a+b ____0．
例3*．分别根据下列条件，利用|a|与|b|表示a与b的和：
(1)a＞0，b＞0；????????????????????(2) a＜0，b＜0；
(3)a＞0，b＜0，|a|＞|b|；?
(4)a＞0，b＜0，|a|＜|b|．＞＜＞＜1．计算：
(1)(-10)+(+6)；????? (2)(+12)+(-4)；???
? (3)(-5)+(-7)；???? (4)(+6)+(+9)；
(5)67+(-73)；???????? (6)(-84)+(-59)；???
(7)33+48；?? ?????? (8)(-56)+37．
2．计算：
(1)(-0.9)+(-2.7)；?????? (2)3.8+(-8.4)；???????????????
(3)(-0.5)+3； (4)3.29+1.78；????????????
?? (5)7+(-3.04)；??????????? (6)(-2.9)+(-0.31)；
(7)(-9.18)+6.18；?????? (8)4.23+(-6.77)；??????????
? (9)(-0.78)+0．练一练1．有理数的加法法则，是进行有理数加法运算的依据，运算步骤如下：
(1)先确定和的符号；
(2)再确定和的绝对值．
2．有理数的加法法则
(1)同号两数相加，取相同的符号，并把绝对值相加．
(2)绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值．互为相反数的两数相加得0．
(3)一个数与0相加，仍得这个数．小结再见作业:P48习题2.4 1--2