数学高中苏教版选修(2-3)3.1《独立性检验》课件
文档属性
| 名称 | 数学高中苏教版选修(2-3)3.1《独立性检验》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 384.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-01 21:10:47 | ||
图片预览






文档简介
课件21张PPT。 良乡中学数学组 制作:任宝泉 书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟少 小 不 学 习,老 来 徒 伤 悲 成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感,百分之九十九的汗水!天 才 在 于 勤 奋,努 力 才 能 成 功!勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!什 么 也 不 问 的 人 什 么 也 学 不 到 !!!怀 天 下 , 求 真 知 , 学 做 人普通高中课程标准数学2-3(选修)第三章 统计案例3.1独立性检验3.1 独立性检验2019年1月23日星期三一、复习引入日常生活中我们关心这样一些问题:
1.吸烟与患肺癌之间有无关系?
2.秃顶与心脏病之间有无关系?
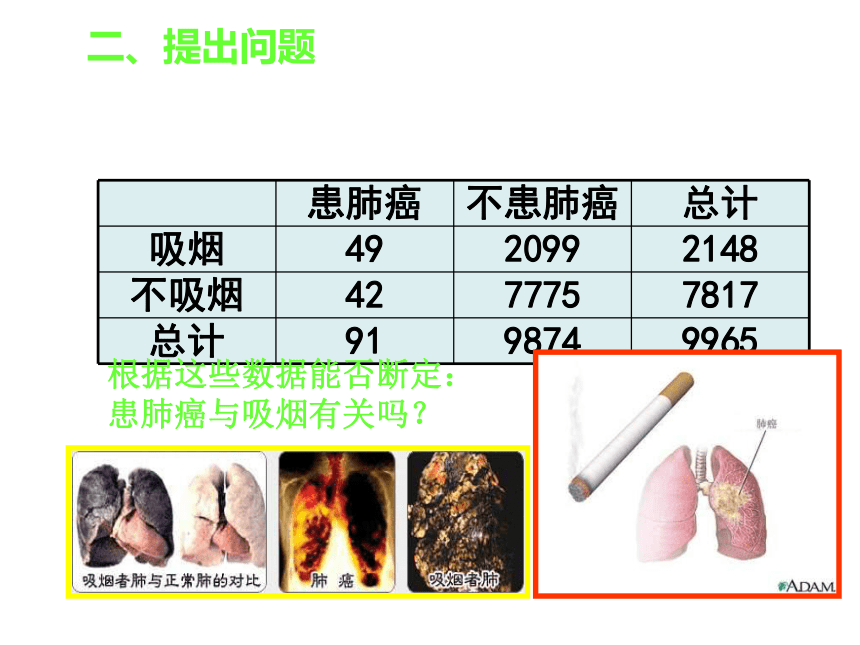
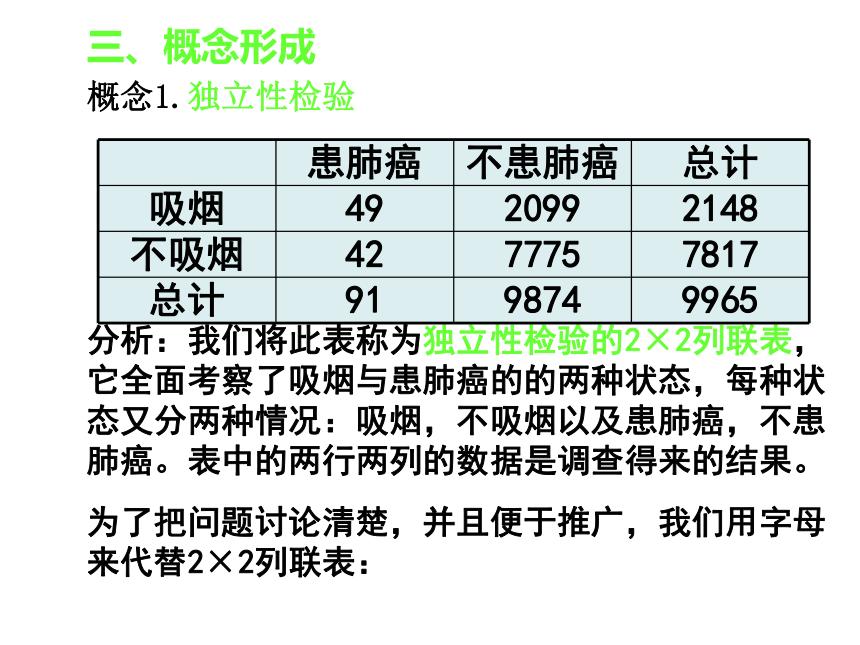
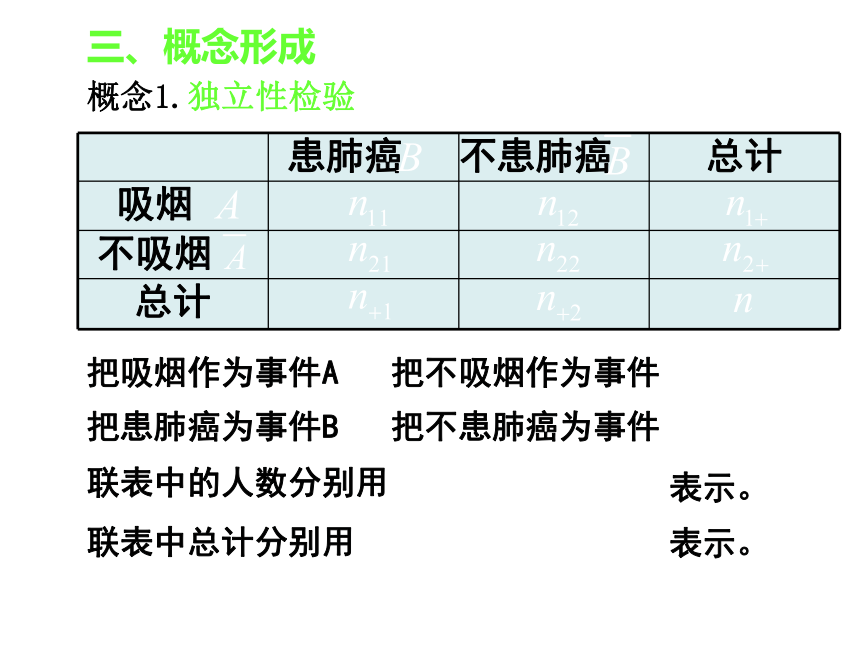
3.性别与喜欢数学课之间有无关系?为了调查吸烟是否对患肺癌有影响,我们应调查哪些数据呢?应该调查吸烟者得肺癌、吸烟者没得肺癌、没吸烟者的肺癌、没吸烟者没得肺癌四种情形的人数。二、提出问题根据这些数据能否断定:患肺癌与吸烟有关吗?某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)三、概念形成概念1.独立性检验分析:我们将此表称为独立性检验的2×2列联表,它全面考察了吸烟与患肺癌的的两种状态,每种状态又分两种情况:吸烟,不吸烟以及患肺癌,不患肺癌。表中的两行两列的数据是调查得来的结果。为了把问题讨论清楚,并且便于推广,我们用字母来代替2×2列联表:三、概念形成概念1.独立性检验把吸烟作为事件A把不吸烟作为事件把患肺癌为事件B把不患肺癌为事件联表中的人数分别用表示。联表中总计分别用表示。三、概念形成概念1.独立性检验(1)首先我们先假设事件A(吸烟)与事件B(患肺癌)是独立的(无关)。由于A,B是相互独立的,应该有P(AB)=P(A)P(B),
即H0:P(AB)=P(A)P(B) ——统计假设。 三、概念形成概念1.独立性检验根据概率的统计定义,上面提到的众多事件的概率都可以用相应的概率来估计。如……由此,与很接近,三、概念形成概念1.独立性检验……由此,与很接近,与也很接近,或者说三、概念形成概念1.独立性检验应该比较小,统计学中采用卡方统计量来描述实际观测值与估计值的差异。从而三、概念形成概念1.独立性检验应该比较小,化简得:用它的大小可以决定是否拒绝原来的统计假设H0。三、概念形成概念1.独立性检验(1)如果算出的“卡方”值较大,就拒绝H0(统计假设),即“事件A与B有关”。(2)两个临界值:3.841与6.635认为事件A与事件B无关。有95%的把握说事件A与B有关。有99%的把握说事件A与B有关。几点说明:(3)使用“卡方”统计量进行独立检验时,统计学要求表中的4个数据都要大于5,在选取样本时要注意这一点。三、概念形成概念1.独立性检验下面利用“卡方”的公式计算吸烟与患肺癌是否有关?由于“卡方”远远大于6.635,这说明有99%以上的把握说明吸烟与患肺癌有关。四、应用举例例1.对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:试根据上述数据比较这两种手术对病人又发心脏病的影响有没有差别?四、应用举例例2.调查者通过询问72名男女大学生在购买食品时是否看营养说明,得到的数据如下表所示:问:大学生的性别与是否看营养说明之间有没有关系?四、应用举例例3.打鼾不仅影响别人休息,而且可能与患某种疾病有关。下表是一次调查所得数据,试问:每一晚都打鼾与患心脏病有关吗?五、课堂练习课本第81页,习题3-1A,1,2,3,4六、课堂总结六、课堂总结七、布置作业课本第81页,习题3-1A,B,
弹性作业:
《新教材新学案》第81~85页下课
1.吸烟与患肺癌之间有无关系?
2.秃顶与心脏病之间有无关系?
3.性别与喜欢数学课之间有无关系?为了调查吸烟是否对患肺癌有影响,我们应调查哪些数据呢?应该调查吸烟者得肺癌、吸烟者没得肺癌、没吸烟者的肺癌、没吸烟者没得肺癌四种情形的人数。二、提出问题根据这些数据能否断定:患肺癌与吸烟有关吗?某肿瘤研究所随机地调查了9965人,得到如下结果(单位:人)三、概念形成概念1.独立性检验分析:我们将此表称为独立性检验的2×2列联表,它全面考察了吸烟与患肺癌的的两种状态,每种状态又分两种情况:吸烟,不吸烟以及患肺癌,不患肺癌。表中的两行两列的数据是调查得来的结果。为了把问题讨论清楚,并且便于推广,我们用字母来代替2×2列联表:三、概念形成概念1.独立性检验把吸烟作为事件A把不吸烟作为事件把患肺癌为事件B把不患肺癌为事件联表中的人数分别用表示。联表中总计分别用表示。三、概念形成概念1.独立性检验(1)首先我们先假设事件A(吸烟)与事件B(患肺癌)是独立的(无关)。由于A,B是相互独立的,应该有P(AB)=P(A)P(B),
即H0:P(AB)=P(A)P(B) ——统计假设。 三、概念形成概念1.独立性检验根据概率的统计定义,上面提到的众多事件的概率都可以用相应的概率来估计。如……由此,与很接近,三、概念形成概念1.独立性检验……由此,与很接近,与也很接近,或者说三、概念形成概念1.独立性检验应该比较小,统计学中采用卡方统计量来描述实际观测值与估计值的差异。从而三、概念形成概念1.独立性检验应该比较小,化简得:用它的大小可以决定是否拒绝原来的统计假设H0。三、概念形成概念1.独立性检验(1)如果算出的“卡方”值较大,就拒绝H0(统计假设),即“事件A与B有关”。(2)两个临界值:3.841与6.635认为事件A与事件B无关。有95%的把握说事件A与B有关。有99%的把握说事件A与B有关。几点说明:(3)使用“卡方”统计量进行独立检验时,统计学要求表中的4个数据都要大于5,在选取样本时要注意这一点。三、概念形成概念1.独立性检验下面利用“卡方”的公式计算吸烟与患肺癌是否有关?由于“卡方”远远大于6.635,这说明有99%以上的把握说明吸烟与患肺癌有关。四、应用举例例1.对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:试根据上述数据比较这两种手术对病人又发心脏病的影响有没有差别?四、应用举例例2.调查者通过询问72名男女大学生在购买食品时是否看营养说明,得到的数据如下表所示:问:大学生的性别与是否看营养说明之间有没有关系?四、应用举例例3.打鼾不仅影响别人休息,而且可能与患某种疾病有关。下表是一次调查所得数据,试问:每一晚都打鼾与患心脏病有关吗?五、课堂练习课本第81页,习题3-1A,1,2,3,4六、课堂总结六、课堂总结七、布置作业课本第81页,习题3-1A,B,
弹性作业:
《新教材新学案》第81~85页下课
