10.3频率与概率 教案(表格式)
文档属性
| 名称 | 10.3频率与概率 教案(表格式) | 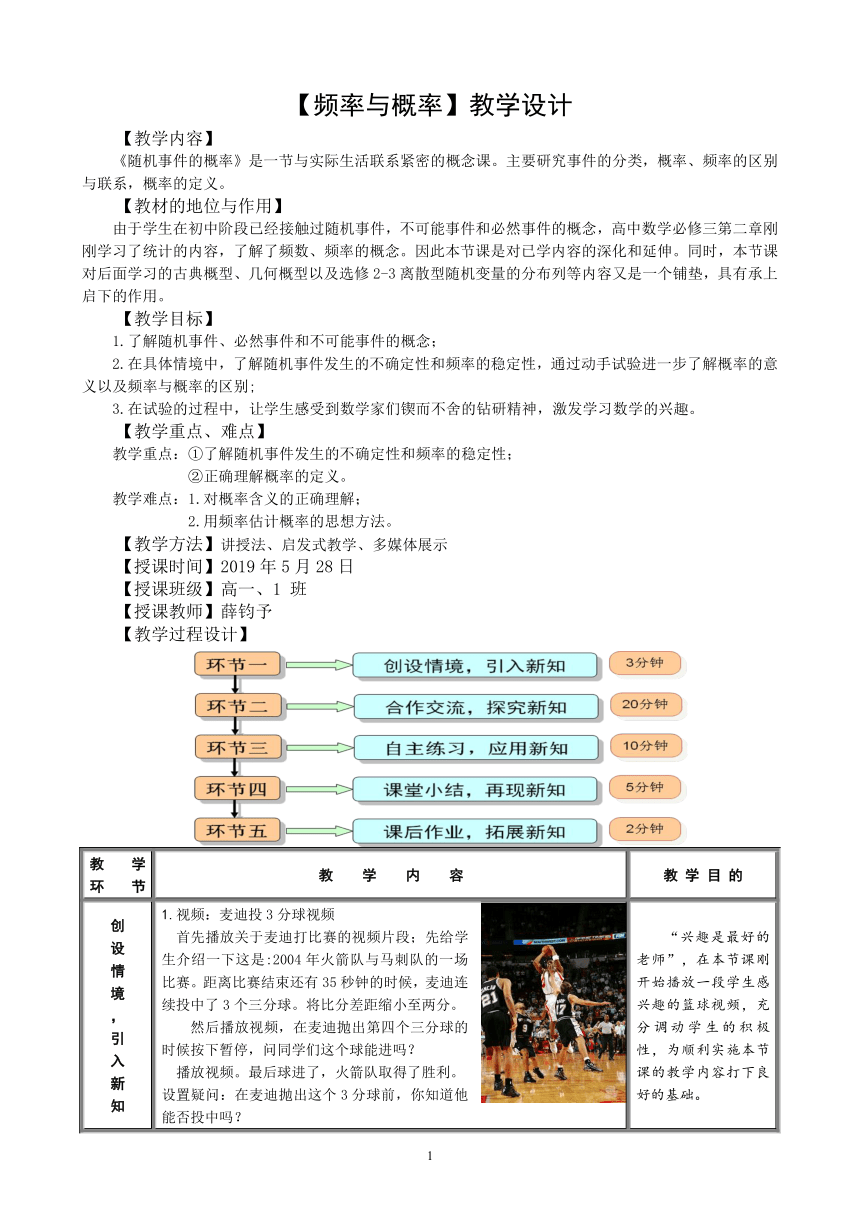 | |
| 格式 | zip | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 09:54:21 | ||
图片预览


文档简介
【频率与概率】教学设计
【教学内容】
《随机事件的概率》是一节与实际生活联系紧密的概念课。主要研究事件的分类,概率、频率的区别与联系,概率的定义。
【教材的地位与作用】
由于学生在初中阶段已经接触过随机事件,不可能事件和必然事件的概念,高中数学必修三第二章刚刚学习了统计的内容,了解了频数、频率的概念。因此本节课是对已学内容的深化和延伸。同时,本节课对后面学习的古典概型、几何概型以及选修2-3离散型随机变量的分布列等内容又是一个铺垫,具有承上启下的作用。
【教学目标】
1.了解随机事件、必然事件和不可能事件的概念;
2.在具体情境中,了解随机事件发生的不确定性和频率的稳定性,通过动手试验进一步了解概率的意义以及频率与概率的区别;
3.在试验的过程中,让学生感受到数学家们锲而不舍的钻研精神,激发学习数学的兴趣。
【教学重点、难点】
教学重点:①了解随机事件发生的不确定性和频率的稳定性;
②正确理解概率的定义。
教学难点:1.对概率含义的正确理解;
2.用频率估计概率的思想方法。
【教学方法】讲授法、启发式教学、多媒体展示
【授课时间】2019年5月28日
【授课班级】高一、1 班
【授课教师】薛钧予
【教学过程设计】
教学环节 教 学 内 容 教 学 目 的
创设情境,引入新知 1.视频:麦迪投3分球视频首先播放关于麦迪打比赛的视频片段;先给学生介绍一下这是:2004年火箭队与马刺队的一场比赛。距离比赛结束还有35秒钟的时候,麦迪连续投中了3个三分球。将比分差距缩小至两分。然后播放视频,在麦迪抛出第四个三分球的时候按下暂停,问同学们这个球能进吗? 播放视频。最后球进了,火箭队取得了胜利。设置疑问:在麦迪抛出这个3分球前,你知道他能否投中吗? “兴趣是最好的老师”,在本节课刚开始播放一段学生感兴趣的篮球视频,充分调动学生的积极性,为顺利实施本节课的教学内容打下良好的基础。
合作交流,探究新知合作交流,探究新知 1.考察下列事件能否发生?(1)导体通电时发热;(2)向上抛出的石头会下落;(3)在标准大气压下水温升高到100°C会沸腾.(4)在没有水分的真空中种子发芽;(5)在常温常压下钢铁融化;(6)(7)某人射击一次命中目标;(8)买一张福利彩票,会中奖;(9)抛掷一个骰字出现的点数为偶数. 2. 复习基本概念:(1)必然事件:在条件S下,一定会发生的事件,叫相对于条件S的必然事件;(2)不可能事件:在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;(3)随机事件:在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件。 3.巩固练习:判断下列事件是什么类型的事件(1)“地球不停地转动”(2)“木柴燃烧,产生能量”(3)“在常温下,石头在一天内风化”(4)“某人射击一次,中靶”(5)“掷一枚硬币,出现正面”(6)“在标准大气压下且温度低于0℃时,雪融化” 4.设置疑问(1)既然投三分球命中是随机事件,那为什么派麦迪投而不是其他篮球运动员?(2)麦迪投三分球命中的可能性比其他篮球运动员命中的可能性大,这一生活经验是如何得到的?5.复习频率的概念:在相同条件下进行n次重复试验,某一事件A出现的次数称为事件A发生的频数;称事件A出现的比例为事件A发生的频率。6.产生矛盾,引出试验 在生活中我们通常用投篮投进的频率来估计投篮投进的可能性大小,那么这种方法是否具有普遍性呢?一、分组投硬币实验(1)试验目的 探究随机事件“抛掷一枚硬币,正面朝上”发生的可能性大小;(规定带数字1的为正面)(2)投币规则 一枚均匀硬币;垂直下抛;离桌面高度大约为30cm;落到桌面上(3)试验要求 每小组选出一位同学抛掷硬币n次,选出一位同学记录出现正面向上的次数m,最后用公式 ,计算出现正面向上的结果并完成下表:小组抛掷的次数正面向上的次数正面向上的比例二、计算模拟掷硬币试验实验的次数正面向上的次数正面向上的比例三、历史上一些数学家的投硬币实验及数据分析图试验结论:在相同条件下,大量重复抛掷硬币试验时,出现正面向上的频率在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5,这个常数0.5就是硬币正面向上发生的可能性大小.1.抽象概括——概率的定义在大量重复进行同一试验时,事件A发生的频率总是接近于某个常数,并在它附近摆动,我们就把这个常数叫做事件A的概率.记作P(A)。2.思考1:在相同条件下,事件A在先后两次试验中发生的频率是否一定相等?事件A在先后两次试验中发生的概率 P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.思考2:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么?3.频率与概率的区别与联系区别:事件A发生的频率fn(A)是变化的,在试验前是不确定的;做同样次数或不同次数试验得到的事件的频率是不同的.事件A发生的概率P(A)是不变的,在试验前是确定的;与每次试验结果无关,与试验次数无关,甚至与做不做试验无关。 它反映的是随机事件发生的可能性大小,随机事件A的概率的取值范围是0课堂小结 知识归纳:1、本节课需掌握的知识:①了解必然事件,不可能事件,随机事件的概念;②理解随机事件的发生在大量重复试验下,呈现规律性;2、必然事件、不可能事件、随机事件是在一定的条件下发生的,当条件变化时,事件的性质也发生变化。3、必然事件与不可能事件可看作随机事件的两种特殊情况.因此,任何事件发生的概率都满足:0≤P(A)≤1。4、随机事件在相同的条件下进行大量的试验时,呈现规律性,且频率 总是接近于常数P(A),称P(A)为事件的概率。 课堂小结,鼓励学生自由发言,说说本节课的收获。一方面培养学生的概括和语言表达能力,另一方面优化了学生的认知结构,明确本节课的收获。
再现新知 练习:下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。(1)完成上面表格:(2)该油菜子发芽的概率约是多少?
课后作业 作业:1.完成课本P113课后练习2.预习:3.1.2概率的意义 课后作业进一步加深概率概念的理解学习。
【板书设计】
3.1.1随机事件的概率
1.必然事件2.不可能事件3.随机事件4.频率 5.试验6.概率7.频率与概率的区别与联系
【教学内容】
《随机事件的概率》是一节与实际生活联系紧密的概念课。主要研究事件的分类,概率、频率的区别与联系,概率的定义。
【教材的地位与作用】
由于学生在初中阶段已经接触过随机事件,不可能事件和必然事件的概念,高中数学必修三第二章刚刚学习了统计的内容,了解了频数、频率的概念。因此本节课是对已学内容的深化和延伸。同时,本节课对后面学习的古典概型、几何概型以及选修2-3离散型随机变量的分布列等内容又是一个铺垫,具有承上启下的作用。
【教学目标】
1.了解随机事件、必然事件和不可能事件的概念;
2.在具体情境中,了解随机事件发生的不确定性和频率的稳定性,通过动手试验进一步了解概率的意义以及频率与概率的区别;
3.在试验的过程中,让学生感受到数学家们锲而不舍的钻研精神,激发学习数学的兴趣。
【教学重点、难点】
教学重点:①了解随机事件发生的不确定性和频率的稳定性;
②正确理解概率的定义。
教学难点:1.对概率含义的正确理解;
2.用频率估计概率的思想方法。
【教学方法】讲授法、启发式教学、多媒体展示
【授课时间】2019年5月28日
【授课班级】高一、1 班
【授课教师】薛钧予
【教学过程设计】
教学环节 教 学 内 容 教 学 目 的
创设情境,引入新知 1.视频:麦迪投3分球视频首先播放关于麦迪打比赛的视频片段;先给学生介绍一下这是:2004年火箭队与马刺队的一场比赛。距离比赛结束还有35秒钟的时候,麦迪连续投中了3个三分球。将比分差距缩小至两分。然后播放视频,在麦迪抛出第四个三分球的时候按下暂停,问同学们这个球能进吗? 播放视频。最后球进了,火箭队取得了胜利。设置疑问:在麦迪抛出这个3分球前,你知道他能否投中吗? “兴趣是最好的老师”,在本节课刚开始播放一段学生感兴趣的篮球视频,充分调动学生的积极性,为顺利实施本节课的教学内容打下良好的基础。
合作交流,探究新知合作交流,探究新知 1.考察下列事件能否发生?(1)导体通电时发热;(2)向上抛出的石头会下落;(3)在标准大气压下水温升高到100°C会沸腾.(4)在没有水分的真空中种子发芽;(5)在常温常压下钢铁融化;(6)(7)某人射击一次命中目标;(8)买一张福利彩票,会中奖;(9)抛掷一个骰字出现的点数为偶数. 2. 复习基本概念:(1)必然事件:在条件S下,一定会发生的事件,叫相对于条件S的必然事件;(2)不可能事件:在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;(3)随机事件:在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件。 3.巩固练习:判断下列事件是什么类型的事件(1)“地球不停地转动”(2)“木柴燃烧,产生能量”(3)“在常温下,石头在一天内风化”(4)“某人射击一次,中靶”(5)“掷一枚硬币,出现正面”(6)“在标准大气压下且温度低于0℃时,雪融化” 4.设置疑问(1)既然投三分球命中是随机事件,那为什么派麦迪投而不是其他篮球运动员?(2)麦迪投三分球命中的可能性比其他篮球运动员命中的可能性大,这一生活经验是如何得到的?5.复习频率的概念:在相同条件下进行n次重复试验,某一事件A出现的次数称为事件A发生的频数;称事件A出现的比例为事件A发生的频率。6.产生矛盾,引出试验 在生活中我们通常用投篮投进的频率来估计投篮投进的可能性大小,那么这种方法是否具有普遍性呢?一、分组投硬币实验(1)试验目的 探究随机事件“抛掷一枚硬币,正面朝上”发生的可能性大小;(规定带数字1的为正面)(2)投币规则 一枚均匀硬币;垂直下抛;离桌面高度大约为30cm;落到桌面上(3)试验要求 每小组选出一位同学抛掷硬币n次,选出一位同学记录出现正面向上的次数m,最后用公式 ,计算出现正面向上的结果并完成下表:小组抛掷的次数正面向上的次数正面向上的比例二、计算模拟掷硬币试验实验的次数正面向上的次数正面向上的比例三、历史上一些数学家的投硬币实验及数据分析图试验结论:在相同条件下,大量重复抛掷硬币试验时,出现正面向上的频率在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5,这个常数0.5就是硬币正面向上发生的可能性大小.1.抽象概括——概率的定义在大量重复进行同一试验时,事件A发生的频率总是接近于某个常数,并在它附近摆动,我们就把这个常数叫做事件A的概率.记作P(A)。2.思考1:在相同条件下,事件A在先后两次试验中发生的频率是否一定相等?事件A在先后两次试验中发生的概率 P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.思考2:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么?3.频率与概率的区别与联系区别:事件A发生的频率fn(A)是变化的,在试验前是不确定的;做同样次数或不同次数试验得到的事件的频率是不同的.事件A发生的概率P(A)是不变的,在试验前是确定的;与每次试验结果无关,与试验次数无关,甚至与做不做试验无关。 它反映的是随机事件发生的可能性大小,随机事件A的概率的取值范围是0
再现新知 练习:下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。(1)完成上面表格:(2)该油菜子发芽的概率约是多少?
课后作业 作业:1.完成课本P113课后练习2.预习:3.1.2概率的意义 课后作业进一步加深概率概念的理解学习。
【板书设计】
3.1.1随机事件的概率
1.必然事件2.不可能事件3.随机事件4.频率 5.试验6.概率7.频率与概率的区别与联系
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
