2022年七年级下学期数学北师大版4.3探索三角形全等的条件(1)课件(共19张ppt)
文档属性
| 名称 | 2022年七年级下学期数学北师大版4.3探索三角形全等的条件(1)课件(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
北师大版七年级下册
4.3 探索三角形全等的条件
(第1课时SSS)
第四章 三角形
1
19
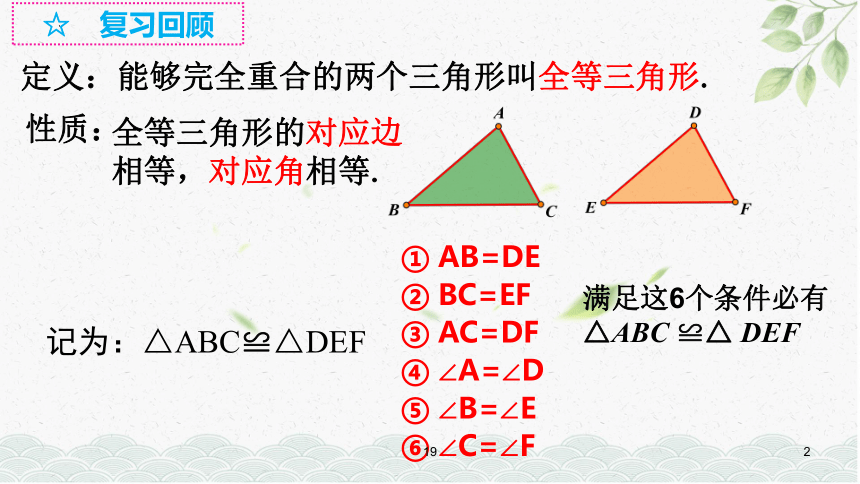
记为:△ABC≌△DEF
☆ 复习回顾
定义:能够完全重合的两个三角形叫全等三角形.
性质:
① AB=DE
② BC=EF
③ AC=DF
④ ∠A=∠D
⑤ ∠B=∠E
⑥ ∠C=∠F
全等三角形的对应边
相等,对应角相等.
满足这6个条件必有
△ABC ≌△ DEF
2
19
如果想画一个与△ABC完全一样的三角形,该怎么画?需要哪些条件?说明理由。
探索全等三角形的条件
一、 只给一个条件
2. 只给一条边时;
A
B
C
1.只给一个角时;
结论:不一定全等.
60°
分类讨论数学思想
3
19
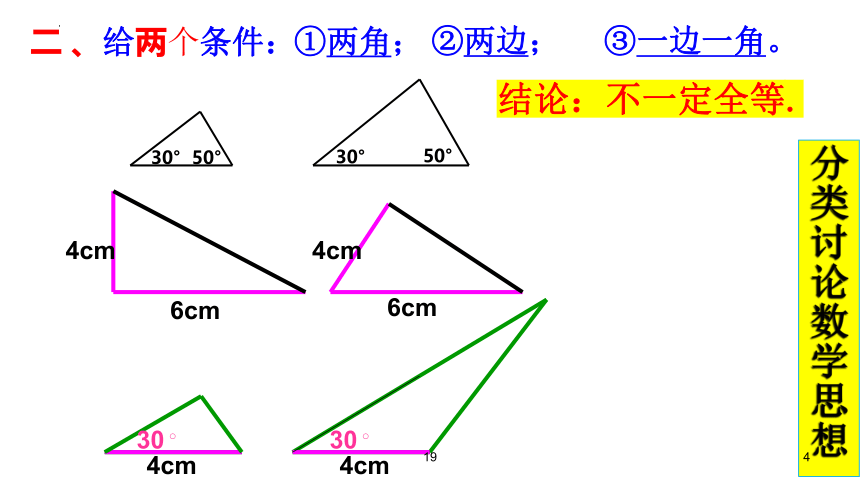
二 、给两个条件:
①两角;
②两边;
③一边一角。
4cm
4cm
30
30
6cm
6cm
4cm
4cm
30°
50°
30°
50°
结论:不一定全等.
分类讨论数学思想
4
19
①三角对应相等;
②三边对应相等;
③两边一角对应相等;
④两角一边对应相等。
二 、给三个条件:
分类讨论数学思想
结论:不一定全等.
5
19
②三条边对应相等:已知两个三角形的三条边都分别为3cm,4cm,6cm,它们一定全等吗?
通过平移、旋转、翻折,得到它们能够完全重合,
也就是说它们是全等的.
3 cm
4 cm
6 cm
3 cm
4 cm
6 cm
3 cm
4 cm
6 cm
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
6
19
两个条件:
①两角对应相等;
②两边对应相等;
③一边一角对应相等.
结论1:只给出一个或两个条件时,三角形不一定全等
一个条件:
①一角对应相等;
②一边对应相等;
总结
三个条件:
①三角对应相等;
②三边对应相等;
③两边一角对应相等;
④两角一边对应相等。
结论2:
三角形不一定全等.
两个三角形全等.
下节课继续探讨.
7
19
画法:
(1)画射线B′M,在射线B′M截取线段B′C′=BC;
(2)以B′为圆心,AB为半径画弧,以C′为圆心,AC为半径画弧,
两弧相交于点A′.
(3)连接A′B′,A′C′得△A′B′C′.
剪下△A′B′C′放在△ABC上,可以看到△A′B′C′≌△ABC.
A
B
C
B′
C′
M
A′
画一个与△ABC全等的三角形.
8
19
两个三角形全等的判定方法1:
用符号表达:
在△ABC和△A′B′C′中,
AB=A′B′, AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′ (SSS)
A
B
C
A′
B′
C′
知识要点
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
指明范围
三个条件
写出结论
注意:对应点要写在相应的位置上.
9
19
典例1 如图在△ABC中,AB=AC,D是BC中点.请说明:(1)△ABD ≌△ACD .
C
B
D
A
解题思路:
隐含条件
②公共边AD
三个条件
①AB=AC
预备条件
③ BD=CD
D是BC的中点
(2)∠B=∠C.
已知条件
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴△ABD≌△ACD(SSS)
10
19
典例2 如图,AB=AC,DB=DC,请说明∠B =∠C.
A
B
C
D
在△ABD和△ACD中,
AB=AC (已知),
DB=DC(已知),
AD=AD(公共边),
∴△ABD≌△ACD (SSS),
解:连接AD.
∴ ∠B =∠C (全等三角形的对应角相等).
11
19
典例3 如图,已知AC=AD,BC=BD,证:AB平分∠DAC.
AC=AD( )
BC=BD( )
——————
AB=AB( )
∴△____≌△ABD( )
∴_______( )
∴AB平分∠DAC.
A
B
C
D
1
2
全等三角形的对应角相等
已知
已知
公共边
SSS
在△ABC与△ABD中
证明:_____________________________
ABC
∠1=∠2
12
19
只要三角形三边的长度确定了,这个三角形的形状和大小就唯一确定了,因此三角形具有稳定性.
探究三角形的稳定性
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
13
19
这节课你学到了什么?
2、三角形全等的条件:
三边对应相等的两个三角形全等(“边边边”或“SSS”)
1、判定三角形全等的条件:
只给出一个条件或两个条件时都不能保证两个三角形全等
3、三角形具有稳定性
证明的书写步骤:1、准备条件:证全等时要用的条件要先证好。2、三角形全等书写三步骤:①写出在哪两个三角形中;②摆出三个条件用逗号隔开;③写出全等结论。
14
19
检测与过关
1.木工师傅在做完门框后为防止变形,常用如图1所示那样钉上两条斜拉的木板条,这样做的数学依据是 ;
2. 如图2,已知AC=DB,要使得△ABC≌△DCB, 只需增加的一个条件是 .
3.如图3,△ABC中,AB=AC,AD是BC边上的中线,
则∠BAD= .
图1 图2 图3
三角形具有稳定性
AB=DC
∠CAD
15
19
∴ △ABC≌ (SSS).
(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
解: △ABC≌△DCB. 理由如下:
AB = CD, AC = BD, =____
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件_________________.
BC
△DCB
BF=CD
4.填空题:
A
B
C
D
=
=
A
E
B D F C
=
=
或 BD=FC
CB
16
19
重点、难点精讲
如图,AC=DF,BC=EF,AD=BE,则∠C与∠F的大小关系怎样?说明理由。
解:∠C=∠F,理由如下:
∵AD=BE(已知)
∴AD+BD=BE+BD(等式的性式)
AB=DE
在△ABC与△DEF中
AC=DF(已知), AB=DE(已证),
BC=EF(已知)
∴△ABC≌△DEF(SSS)
∴∠C=∠F(全等三角形的对应角相等)
17
19
布置作业
1.如图,已知AB=CD、AD=CB.
则∠A与∠C相等吗?为什么?
B
C
D
A
2.如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌ △ ADC.
C
A
B
D
E
3.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠1=∠2吗?为什么?
1
2
18
19
课外思考题
4.已知:如图,AB=AD,BC=DE,AC=AE,BC交DE于点M、交AD于点N。
求证:∠ 1 = ∠ 2 = ∠3.
19
19
北师大版七年级下册
4.3 探索三角形全等的条件
(第1课时SSS)
第四章 三角形
1
19
记为:△ABC≌△DEF
☆ 复习回顾
定义:能够完全重合的两个三角形叫全等三角形.
性质:
① AB=DE
② BC=EF
③ AC=DF
④ ∠A=∠D
⑤ ∠B=∠E
⑥ ∠C=∠F
全等三角形的对应边
相等,对应角相等.
满足这6个条件必有
△ABC ≌△ DEF
2
19
如果想画一个与△ABC完全一样的三角形,该怎么画?需要哪些条件?说明理由。
探索全等三角形的条件
一、 只给一个条件
2. 只给一条边时;
A
B
C
1.只给一个角时;
结论:不一定全等.
60°
分类讨论数学思想
3
19
二 、给两个条件:
①两角;
②两边;
③一边一角。
4cm
4cm
30
30
6cm
6cm
4cm
4cm
30°
50°
30°
50°
结论:不一定全等.
分类讨论数学思想
4
19
①三角对应相等;
②三边对应相等;
③两边一角对应相等;
④两角一边对应相等。
二 、给三个条件:
分类讨论数学思想
结论:不一定全等.
5
19
②三条边对应相等:已知两个三角形的三条边都分别为3cm,4cm,6cm,它们一定全等吗?
通过平移、旋转、翻折,得到它们能够完全重合,
也就是说它们是全等的.
3 cm
4 cm
6 cm
3 cm
4 cm
6 cm
3 cm
4 cm
6 cm
结论:三边对应相等的两个三角形全等.
可简写为边边边或SSS
6
19
两个条件:
①两角对应相等;
②两边对应相等;
③一边一角对应相等.
结论1:只给出一个或两个条件时,三角形不一定全等
一个条件:
①一角对应相等;
②一边对应相等;
总结
三个条件:
①三角对应相等;
②三边对应相等;
③两边一角对应相等;
④两角一边对应相等。
结论2:
三角形不一定全等.
两个三角形全等.
下节课继续探讨.
7
19
画法:
(1)画射线B′M,在射线B′M截取线段B′C′=BC;
(2)以B′为圆心,AB为半径画弧,以C′为圆心,AC为半径画弧,
两弧相交于点A′.
(3)连接A′B′,A′C′得△A′B′C′.
剪下△A′B′C′放在△ABC上,可以看到△A′B′C′≌△ABC.
A
B
C
B′
C′
M
A′
画一个与△ABC全等的三角形.
8
19
两个三角形全等的判定方法1:
用符号表达:
在△ABC和△A′B′C′中,
AB=A′B′, AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′ (SSS)
A
B
C
A′
B′
C′
知识要点
三边对应相等的两个三角形全等.简写为“边边边”或“SSS”.
指明范围
三个条件
写出结论
注意:对应点要写在相应的位置上.
9
19
典例1 如图在△ABC中,AB=AC,D是BC中点.请说明:(1)△ABD ≌△ACD .
C
B
D
A
解题思路:
隐含条件
②公共边AD
三个条件
①AB=AC
预备条件
③ BD=CD
D是BC的中点
(2)∠B=∠C.
已知条件
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴△ABD≌△ACD(SSS)
10
19
典例2 如图,AB=AC,DB=DC,请说明∠B =∠C.
A
B
C
D
在△ABD和△ACD中,
AB=AC (已知),
DB=DC(已知),
AD=AD(公共边),
∴△ABD≌△ACD (SSS),
解:连接AD.
∴ ∠B =∠C (全等三角形的对应角相等).
11
19
典例3 如图,已知AC=AD,BC=BD,证:AB平分∠DAC.
AC=AD( )
BC=BD( )
——————
AB=AB( )
∴△____≌△ABD( )
∴_______( )
∴AB平分∠DAC.
A
B
C
D
1
2
全等三角形的对应角相等
已知
已知
公共边
SSS
在△ABC与△ABD中
证明:_____________________________
ABC
∠1=∠2
12
19
只要三角形三边的长度确定了,这个三角形的形状和大小就唯一确定了,因此三角形具有稳定性.
探究三角形的稳定性
这就是说,三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形边长确定,其形状和大小就确定了”.
13
19
这节课你学到了什么?
2、三角形全等的条件:
三边对应相等的两个三角形全等(“边边边”或“SSS”)
1、判定三角形全等的条件:
只给出一个条件或两个条件时都不能保证两个三角形全等
3、三角形具有稳定性
证明的书写步骤:1、准备条件:证全等时要用的条件要先证好。2、三角形全等书写三步骤:①写出在哪两个三角形中;②摆出三个条件用逗号隔开;③写出全等结论。
14
19
检测与过关
1.木工师傅在做完门框后为防止变形,常用如图1所示那样钉上两条斜拉的木板条,这样做的数学依据是 ;
2. 如图2,已知AC=DB,要使得△ABC≌△DCB, 只需增加的一个条件是 .
3.如图3,△ABC中,AB=AC,AD是BC边上的中线,
则∠BAD= .
图1 图2 图3
三角形具有稳定性
AB=DC
∠CAD
15
19
∴ △ABC≌ (SSS).
(1)如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由.
解: △ABC≌△DCB. 理由如下:
AB = CD, AC = BD, =____
(2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要使△ABF≌△ECD ,
还需要条件_________________.
BC
△DCB
BF=CD
4.填空题:
A
B
C
D
=
=
A
E
B D F C
=
=
或 BD=FC
CB
16
19
重点、难点精讲
如图,AC=DF,BC=EF,AD=BE,则∠C与∠F的大小关系怎样?说明理由。
解:∠C=∠F,理由如下:
∵AD=BE(已知)
∴AD+BD=BE+BD(等式的性式)
AB=DE
在△ABC与△DEF中
AC=DF(已知), AB=DE(已证),
BC=EF(已知)
∴△ABC≌△DEF(SSS)
∴∠C=∠F(全等三角形的对应角相等)
17
19
布置作业
1.如图,已知AB=CD、AD=CB.
则∠A与∠C相等吗?为什么?
B
C
D
A
2.如图,AB=AC,AE=AD,BD=CE,
求证:△AEB ≌ △ ADC.
C
A
B
D
E
3.已知:AC、BD相交于点O,且AB=DC,AC=DB,那么∠1=∠2吗?为什么?
1
2
18
19
课外思考题
4.已知:如图,AB=AD,BC=DE,AC=AE,BC交DE于点M、交AD于点N。
求证:∠ 1 = ∠ 2 = ∠3.
19
19
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
