苏科版数学八年级下册8-3频率与概率课件(14张ppt)
文档属性
| 名称 | 苏科版数学八年级下册8-3频率与概率课件(14张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 945.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 12:42:47 | ||
图片预览




文档简介
(共14张PPT)
频率与概率(2)
同学们,在硬地上掷1枚图钉,通常会出现哪些情况?
你认为钉尖着地和钉尖不着地的可能性一样吗?
创设情境
(1)任意掷1枚图钉,你认为是“钉尖着地”的可能性大,还是“钉尖不着地”的可能性大?
猜想
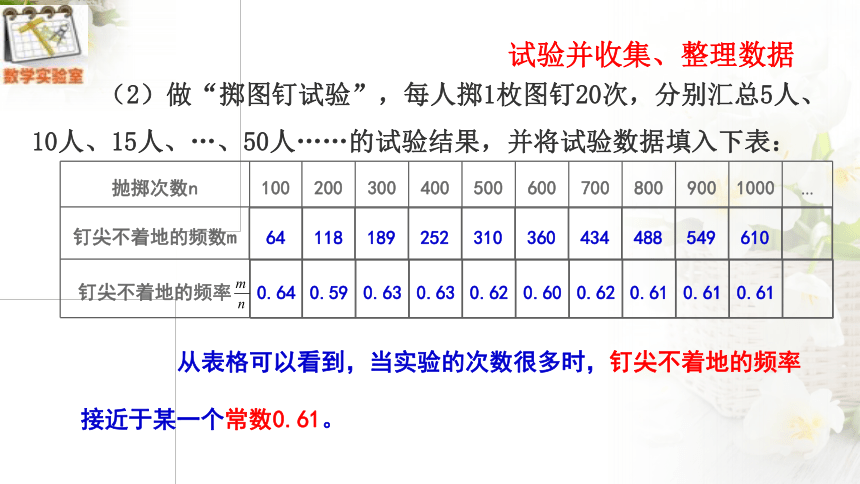
(2)做“掷图钉试验”,每人掷1枚图钉20次,分别汇总5人、
10人、15人、…、50人……的试验结果,并将试验数据填入下表:
抛掷次数n 100 200 300 400 500 600 700 800 900 1000 …
钉尖不着地的频数m
钉尖不着地的频率
0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
64 118 189 252 310 360 434 488 549 610
试验并收集、整理数据
从表格可以看到,当实验的次数很多时,钉尖不着地的频率
接近于某一个常数0.61。
抛掷次数n 100 200 300 400 500 600 700 800 900 1000 …
钉尖不着地的频数m
钉尖不着地的频率
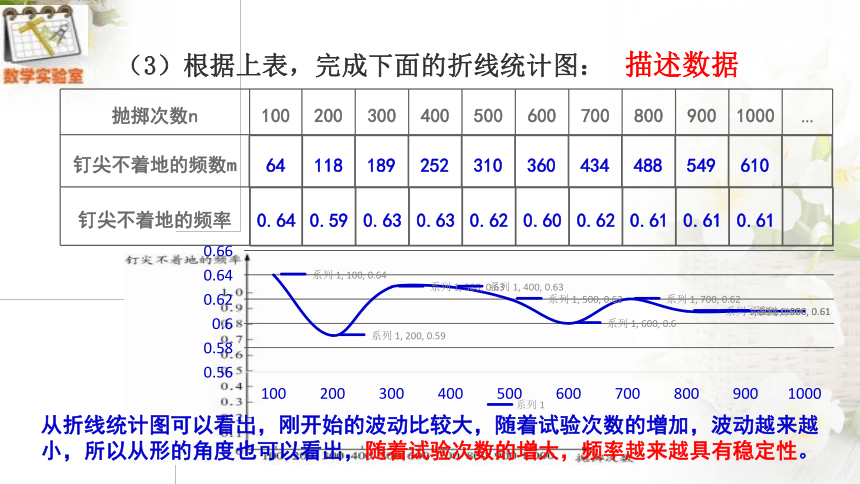
(3)根据上表,完成下面的折线统计图:
描述数据
0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
64 118 189 252 310 360 434 488 549 610
从折线统计图可以看出,刚开始的波动比较大,随着试验次数的增加,波动越来越
小,所以从形的角度也可以看出,随着试验次数的增大,频率越来越具有稳定性。
试验并收集整理描述数据
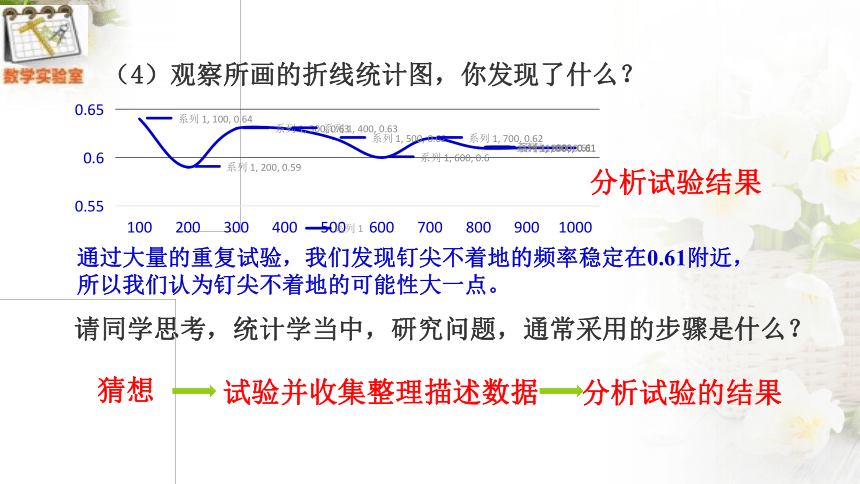
(4)观察所画的折线统计图,你发现了什么?
分析试验结果
通过大量的重复试验,我们发现钉尖不着地的频率稳定在0.61附近,
所以我们认为钉尖不着地的可能性大一点。
分析试验的结果
请同学思考,统计学当中,研究问题,通常采用的步骤是什么?
猜想
一般地,在一定条件下大量重复进行同一试验时,事件A发生的频率会
稳定在某一个常数 附近摆动,这个常数就是事件A发生的概率P(A)。
(重复试验要在相同条件下进行)
小结提升
事实上,事件A发生的概率P(A)的精确值(即这个常数)还是未知的,
但在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值。
(即把试验次数最多的频率值的最后一个有效数字四舍五入,作为概率的近似值)
例如,根据统计学家历次做“抛掷质地均匀的硬币试验”的结果,可以估计
“正面朝上”的概率为0.5;根据“掷图钉试验”的结果,可以估计“钉尖不
着地”的概率为0.61。为什么试验的结果不具有等可能性?
某种绿豆在相同条件下发芽试验的结果如下:
(1)计算并填写表中绿豆发芽的频率;
(2)画出绿豆发芽频率的折线统计图;
(3)这种绿豆发芽的概率的估计值是多少?
每批粒数n 2 5 10 50 100 500 1000 1500 2000 3000 …
发芽的频数m 2 4 9 44 92 463 928 1396 1866 2794
发芽的频率
典型例题
1 0.8 0.9 0.88 0.92 0.926 0.928 0.93 0.933 0.931
通过表格和折线统计图可以看出,当试验的
绿豆粒数很多时,该批绿豆发芽的频率接近
一个常数0.93,并在它的附近摆动,
所以我们估计绿豆发芽的概率约为0.93.
一个随机事件虽具有随机性,有一定的偶然性,但其存在统计规律,
在大量重复试验中,这个随机事件发生的频率具有稳定性,而这个稳定性
是必然的,这就是偶然性与必然性的对立统一。
通过刚才的两个实验,你能说说频率的变化规律吗?
频率与概率又有什么关系
频率与概率之间的关系:在一定条件下,大量重复试验时,事件
发生的频率会在一个常数附近摆动,并随着试验次数增多,摆动的幅度
会减小,这个常数就是其概率的估计值。
1.某种油菜籽在相同条件下的发芽试验结果如下:
(1)填写表中的空格;
(2)画出这种油菜籽发芽频率的折线统计图;
(3)这种油菜籽发芽的概率的估计值是多少?
每批粒数n 100 300 400 600 1000 2020 3000
发芽的频数m 96 283 344 552 948 1912 2848
发芽的频率
课堂训练
0.96 0.943 0.86 0.92 0.948 0.947 0.949
估计油菜籽发芽的
概率约为0.95
2.小明在做图钉落地后钉尖着地的频率有多大,大量实验重复试验后,
发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着实验次数的增加,钉尖着地的频率稳定在0.4附近
C.钉尖着地的概率约为0.4
D.前20次实验结束后,钉尖着地的次数一定是8次
课堂训练
D
3.在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只,某小
组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,
不断重复,右表是活动中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
C
4.在一个不透明的布袋中,装有红色、白色玻璃球共60个,除颜
色外其它完全相同,小明通过多次摸球试验后发现,其中摸到红
球的频率稳定在20%左右,则口袋中红色球可能有( )个
A.5个 B.10个 C.12个 D.48个
课堂训练
C
5.一个箱子中放有a个除颜色外完全相同的球,这a个球中只有3个
红球。每次将球搅匀后任意摸出一个球,记下颜色再放回。通过
大量重复摸球试验后发现,摸到红球的频率稳定在20﹪附近,
那么可以估计a的值大约是 。
15
6.对下列说法谈谈你的看法:
(1)一位同学在做抛掷硬币的实验,做10次实验,其中3次正面
朝上,由此他估计正面朝上的概率是30%;
(2)有人买1张彩票就能中大奖,有的人买100张也不中奖,
因此,所谓的中奖概率都是无稽之谈.
课堂训练
实验次数太少,
没有代表性。
中奖是个随机事件,随机事件的发生与否我们无法预测,
但中奖率是客观存在的。中奖率可以了解中奖这件
事发生的频繁程度。
今天你学到了什么?
频率与概率(2)
同学们,在硬地上掷1枚图钉,通常会出现哪些情况?
你认为钉尖着地和钉尖不着地的可能性一样吗?
创设情境
(1)任意掷1枚图钉,你认为是“钉尖着地”的可能性大,还是“钉尖不着地”的可能性大?
猜想
(2)做“掷图钉试验”,每人掷1枚图钉20次,分别汇总5人、
10人、15人、…、50人……的试验结果,并将试验数据填入下表:
抛掷次数n 100 200 300 400 500 600 700 800 900 1000 …
钉尖不着地的频数m
钉尖不着地的频率
0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
64 118 189 252 310 360 434 488 549 610
试验并收集、整理数据
从表格可以看到,当实验的次数很多时,钉尖不着地的频率
接近于某一个常数0.61。
抛掷次数n 100 200 300 400 500 600 700 800 900 1000 …
钉尖不着地的频数m
钉尖不着地的频率
(3)根据上表,完成下面的折线统计图:
描述数据
0.64 0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
64 118 189 252 310 360 434 488 549 610
从折线统计图可以看出,刚开始的波动比较大,随着试验次数的增加,波动越来越
小,所以从形的角度也可以看出,随着试验次数的增大,频率越来越具有稳定性。
试验并收集整理描述数据
(4)观察所画的折线统计图,你发现了什么?
分析试验结果
通过大量的重复试验,我们发现钉尖不着地的频率稳定在0.61附近,
所以我们认为钉尖不着地的可能性大一点。
分析试验的结果
请同学思考,统计学当中,研究问题,通常采用的步骤是什么?
猜想
一般地,在一定条件下大量重复进行同一试验时,事件A发生的频率会
稳定在某一个常数 附近摆动,这个常数就是事件A发生的概率P(A)。
(重复试验要在相同条件下进行)
小结提升
事实上,事件A发生的概率P(A)的精确值(即这个常数)还是未知的,
但在实际工作中,人们常把试验次数很大时事件发生的频率作为概率的近似值。
(即把试验次数最多的频率值的最后一个有效数字四舍五入,作为概率的近似值)
例如,根据统计学家历次做“抛掷质地均匀的硬币试验”的结果,可以估计
“正面朝上”的概率为0.5;根据“掷图钉试验”的结果,可以估计“钉尖不
着地”的概率为0.61。为什么试验的结果不具有等可能性?
某种绿豆在相同条件下发芽试验的结果如下:
(1)计算并填写表中绿豆发芽的频率;
(2)画出绿豆发芽频率的折线统计图;
(3)这种绿豆发芽的概率的估计值是多少?
每批粒数n 2 5 10 50 100 500 1000 1500 2000 3000 …
发芽的频数m 2 4 9 44 92 463 928 1396 1866 2794
发芽的频率
典型例题
1 0.8 0.9 0.88 0.92 0.926 0.928 0.93 0.933 0.931
通过表格和折线统计图可以看出,当试验的
绿豆粒数很多时,该批绿豆发芽的频率接近
一个常数0.93,并在它的附近摆动,
所以我们估计绿豆发芽的概率约为0.93.
一个随机事件虽具有随机性,有一定的偶然性,但其存在统计规律,
在大量重复试验中,这个随机事件发生的频率具有稳定性,而这个稳定性
是必然的,这就是偶然性与必然性的对立统一。
通过刚才的两个实验,你能说说频率的变化规律吗?
频率与概率又有什么关系
频率与概率之间的关系:在一定条件下,大量重复试验时,事件
发生的频率会在一个常数附近摆动,并随着试验次数增多,摆动的幅度
会减小,这个常数就是其概率的估计值。
1.某种油菜籽在相同条件下的发芽试验结果如下:
(1)填写表中的空格;
(2)画出这种油菜籽发芽频率的折线统计图;
(3)这种油菜籽发芽的概率的估计值是多少?
每批粒数n 100 300 400 600 1000 2020 3000
发芽的频数m 96 283 344 552 948 1912 2848
发芽的频率
课堂训练
0.96 0.943 0.86 0.92 0.948 0.947 0.949
估计油菜籽发芽的
概率约为0.95
2.小明在做图钉落地后钉尖着地的频率有多大,大量实验重复试验后,
发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着实验次数的增加,钉尖着地的频率稳定在0.4附近
C.钉尖着地的概率约为0.4
D.前20次实验结束后,钉尖着地的次数一定是8次
课堂训练
D
3.在一个不透明的口袋里,装有仅颜色不同的黑球、白球若干只,某小
组做摸球实验:将球搅匀后从中随机摸出一个,记下颜色,再放入袋中,
不断重复,右表是活动中的一组数据,则摸到白球的概率约是( )
A.0.4 B.0.5 C.0.6 D.0.7
摸球的次数n 100 150 200 500 800 1000
摸到白球的次数m 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
C
4.在一个不透明的布袋中,装有红色、白色玻璃球共60个,除颜
色外其它完全相同,小明通过多次摸球试验后发现,其中摸到红
球的频率稳定在20%左右,则口袋中红色球可能有( )个
A.5个 B.10个 C.12个 D.48个
课堂训练
C
5.一个箱子中放有a个除颜色外完全相同的球,这a个球中只有3个
红球。每次将球搅匀后任意摸出一个球,记下颜色再放回。通过
大量重复摸球试验后发现,摸到红球的频率稳定在20﹪附近,
那么可以估计a的值大约是 。
15
6.对下列说法谈谈你的看法:
(1)一位同学在做抛掷硬币的实验,做10次实验,其中3次正面
朝上,由此他估计正面朝上的概率是30%;
(2)有人买1张彩票就能中大奖,有的人买100张也不中奖,
因此,所谓的中奖概率都是无稽之谈.
课堂训练
实验次数太少,
没有代表性。
中奖是个随机事件,随机事件的发生与否我们无法预测,
但中奖率是客观存在的。中奖率可以了解中奖这件
事发生的频繁程度。
今天你学到了什么?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
