人教版(2012)八年级下册数学18.2特殊的平行四边形 矩形 课件 (共22张PPT)
文档属性
| 名称 | 人教版(2012)八年级下册数学18.2特殊的平行四边形 矩形 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 12:59:22 | ||
图片预览



文档简介
(共22张PPT)
18.2.1 特殊的平行四边形—矩形
平行四边形的性质
边
对角线
角
平行四边形的对边平行;
平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的邻角互补.
平行四边形的对角线互相平分;
知识回顾
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
矩形的定义
第五节矩形菱形
生活常见的矩形
教科书封面
第五节矩形菱形
生活常见的矩形
平板电脑
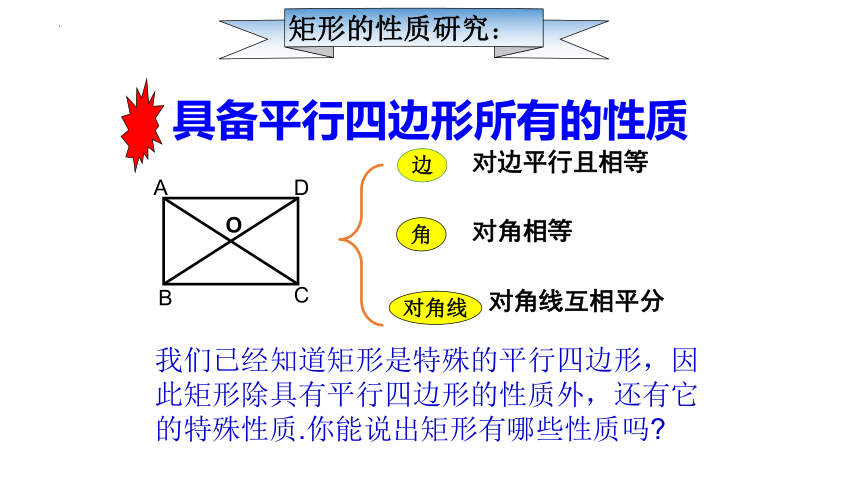
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
矩形的性质研究:
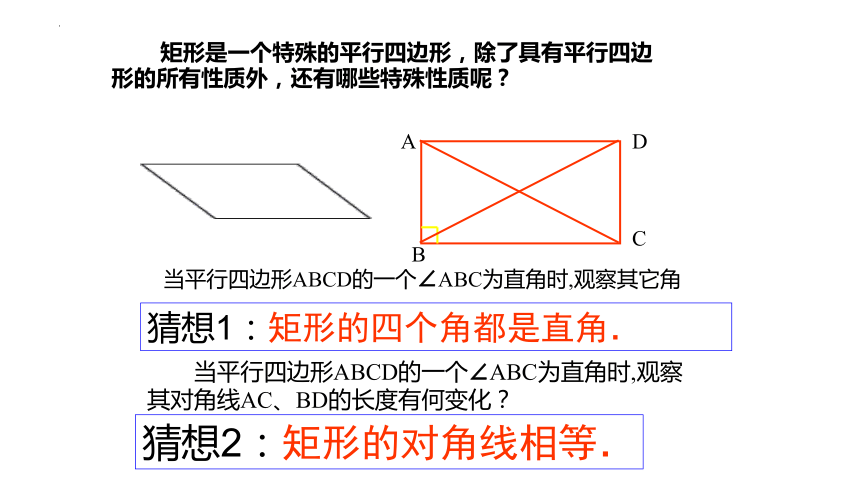
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
当平行四边形ABCD的一个∠ABC为直角时,观察其它角
当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化?
B
A
D
C
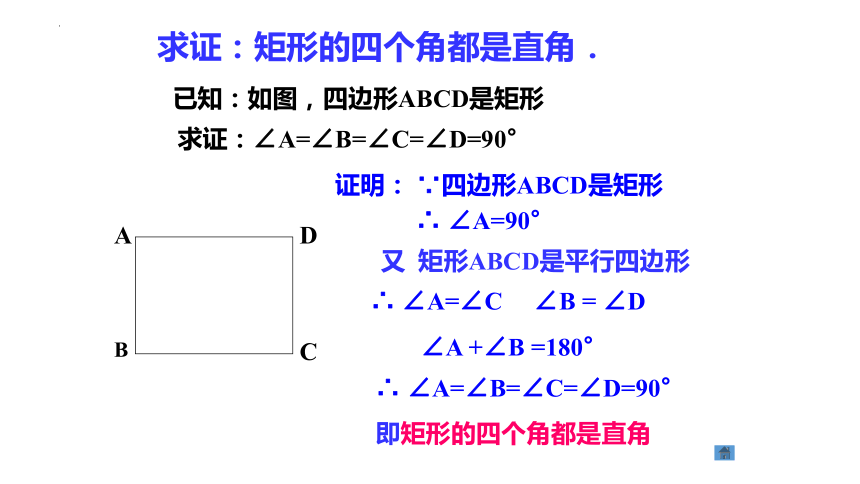
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
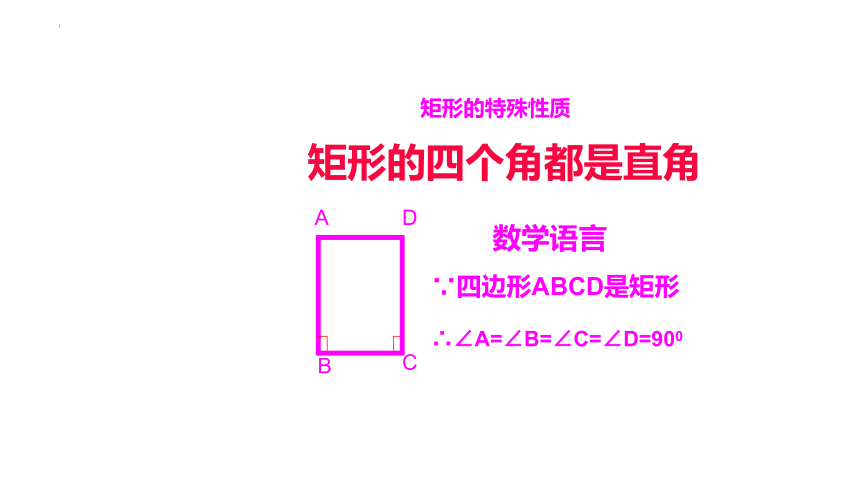
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形的特殊性质
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
A
B
C
D
边
对角线
角
A
B
C
D
O
矩形的性质:
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
AB CD;AD BC
∠A=∠B=∠C=∠D=90°
OA=OC = OB=OD
边 角 对角线
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
这是矩形所特有的性质
知识讲解
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
生活链接---投圈游戏
A
B
C
D
O
C
B
A
D
证明:延长BO至D,使OD=BO,
连结AD、DC。
∵AO=OC,BO=OD
∴四边形ABCD是平行四边形。
∵∠ABC=90°
∴平行四边形ABCD是矩形。
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线。
求证:BO= AC?
∴BO= BD= AC
直角三角形的性质定理2
直角三角形斜边上的中线等于斜边的一半。
C
B
A
O
例1
如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm,求AC的长。
解:
所以,AC的长为12cm。
∵四边形ABCD是矩形,
∴AC=BD,AC=2AO,BD=2BO,
∴AO=BO
∵∠BOC=120°
从而∠AOB=60°
∴△ABO为等边三角形。
从而AO=AB=6(cm),
∴AC=2AB=12(cm)。
[百色中考]如图,在矩形ABCD中,E,F分别是AD,BC的中点,CE,AF分别交DB于G,H两点.
求证:(1)四边形AFCE是平行四边形;
(2)EG=HF.
又∵AB∥CD
∴∠EDG=∠FBH
在△DEG和△BHF中
∴△DEG≌△BHF(AAS)
∴ EG=HF
∵E,F分别是AD,BC的中点
∴DE=BF
证明:(2) ∵四边形AFCE是平行四边形
∴CE∥AF
∴∠DGE=∠AHD=∠BHF
【中考链接】
合作探究
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD.
1、如图,在 ABCD中,E,F分别是AB,DC边上的点,且AE=CF, ∠DEB=90°,求证:四边形DEBF是矩形.
∵∠DEB=90°,
∴四边形DEBF是矩形.
∴四边形BEDF是平行四边形.
∵AE=CF,
∴AB-AE=CD-CF.
∴BE=DF.
独立思考
【知识巩固】
1、判断下列命题是否是真命题?
(1)平行四边形的两条对角线的长度相等。
(2)矩形相邻的两个角的度数相等。
(3)矩形的两条对角线互相平分。
(4)矩形的对角线平分它的一组对角。
假命题
真命题
真命题
假命题
课堂练习
2、已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
O
A
B
C
D
E
我们的收获是:
1.有一个角是直角的平行四边形叫做矩形。
2.矩形的性质:
(1)对边平行且相等;
(2)四个角都是直角;
(3)对角线相等且平分;
3.直角三角形斜边上的中线等于斜边的一半。
小结
18.2.1 特殊的平行四边形—矩形
平行四边形的性质
边
对角线
角
平行四边形的对边平行;
平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的邻角互补.
平行四边形的对角线互相平分;
知识回顾
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
矩形的定义
第五节矩形菱形
生活常见的矩形
教科书封面
第五节矩形菱形
生活常见的矩形
平板电脑
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
矩形的性质研究:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
当平行四边形ABCD的一个∠ABC为直角时,观察其它角
当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化?
B
A
D
C
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明: ∵四边形ABCD是矩形
∴ ∠A=90°
又 矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的特殊性质
矩形的四个角都是直角
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=900
已知:如图,四边形ABCD是矩形
求证:AC = BD
A
B
C
D
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
求证:矩形的对角线相等
矩形的特殊性质
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
A
B
C
D
边
对角线
角
A
B
C
D
O
矩形的性质:
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
AB CD;AD BC
∠A=∠B=∠C=∠D=90°
OA=OC = OB=OD
边 角 对角线
平行四 边形
矩形
比一比,知关系
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
这是矩形所特有的性质
知识讲解
公平,因为OA=OC=OB=OD
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗 为什么?
O
A
B
C
D
生活链接---投圈游戏
A
B
C
D
O
C
B
A
D
证明:延长BO至D,使OD=BO,
连结AD、DC。
∵AO=OC,BO=OD
∴四边形ABCD是平行四边形。
∵∠ABC=90°
∴平行四边形ABCD是矩形。
∴AC=BD
已知:在Rt△ABC中,∠ABC=90°,BO是AC上的中线。
求证:BO= AC?
∴BO= BD= AC
直角三角形的性质定理2
直角三角形斜边上的中线等于斜边的一半。
C
B
A
O
例1
如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm,求AC的长。
解:
所以,AC的长为12cm。
∵四边形ABCD是矩形,
∴AC=BD,AC=2AO,BD=2BO,
∴AO=BO
∵∠BOC=120°
从而∠AOB=60°
∴△ABO为等边三角形。
从而AO=AB=6(cm),
∴AC=2AB=12(cm)。
[百色中考]如图,在矩形ABCD中,E,F分别是AD,BC的中点,CE,AF分别交DB于G,H两点.
求证:(1)四边形AFCE是平行四边形;
(2)EG=HF.
又∵AB∥CD
∴∠EDG=∠FBH
在△DEG和△BHF中
∴△DEG≌△BHF(AAS)
∴ EG=HF
∵E,F分别是AD,BC的中点
∴DE=BF
证明:(2) ∵四边形AFCE是平行四边形
∴CE∥AF
∴∠DGE=∠AHD=∠BHF
【中考链接】
合作探究
证明:∵四边形ABCD是平行四边形
∴AB=CD,AB∥CD.
1、如图,在 ABCD中,E,F分别是AB,DC边上的点,且AE=CF, ∠DEB=90°,求证:四边形DEBF是矩形.
∵∠DEB=90°,
∴四边形DEBF是矩形.
∴四边形BEDF是平行四边形.
∵AE=CF,
∴AB-AE=CD-CF.
∴BE=DF.
独立思考
【知识巩固】
1、判断下列命题是否是真命题?
(1)平行四边形的两条对角线的长度相等。
(2)矩形相邻的两个角的度数相等。
(3)矩形的两条对角线互相平分。
(4)矩形的对角线平分它的一组对角。
假命题
真命题
真命题
假命题
课堂练习
2、已知:如图,过矩形ABCD的顶点作CE//BD,交AB的延长线于E。
求证:∠CAE=∠CEA
O
A
B
C
D
E
我们的收获是:
1.有一个角是直角的平行四边形叫做矩形。
2.矩形的性质:
(1)对边平行且相等;
(2)四个角都是直角;
(3)对角线相等且平分;
3.直角三角形斜边上的中线等于斜边的一半。
小结
