人教版数学九年级下册 第28章本章复习与测试 课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级下册 第28章本章复习与测试 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 983.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
锐角三角函数复习小结
复习目标: 1.复习本章的重点内容,整理本章知识,形成知识 体系; 2.熟练掌握直角三角形的解法,并用相关知识解决 一些简单的实际问题,进一步加深对锐角三角函 数的认识.
复习重点: 梳理本章的知识结构体系,并灵活运用锐角三角函数和解直角三角形的知识解决问题.
知识梳理
问题1 请同学们解答下列问题:
(1)我们已学过哪几种锐角三角函数?写出如图所示的直角三角形中两个锐角的三角函数.
C
A
B
知识梳理
问题1 请同学们解答下列问题:
(2)特殊角的三角形函数值是什么?
C
A
B
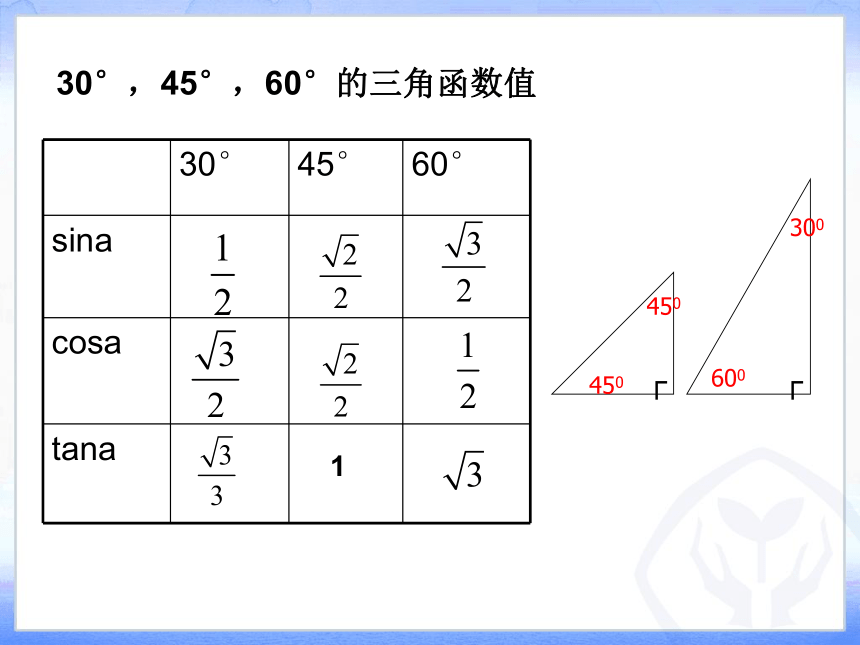
30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
┌
┌
450
450
300
600
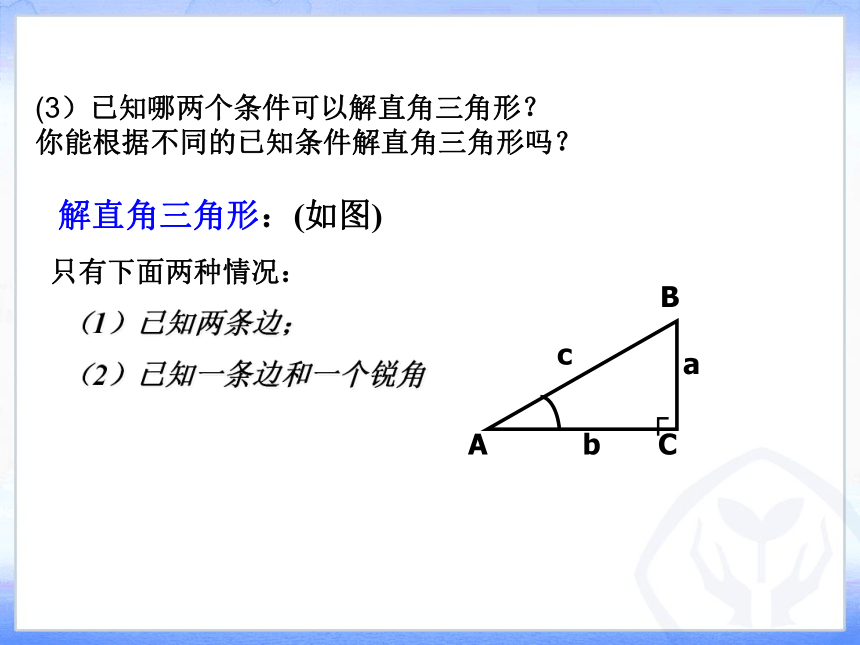
解直角三角形:(如图)
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
(3)已知哪两个条件可以解直角三角形?
你能根据不同的已知条件解直角三角形吗?
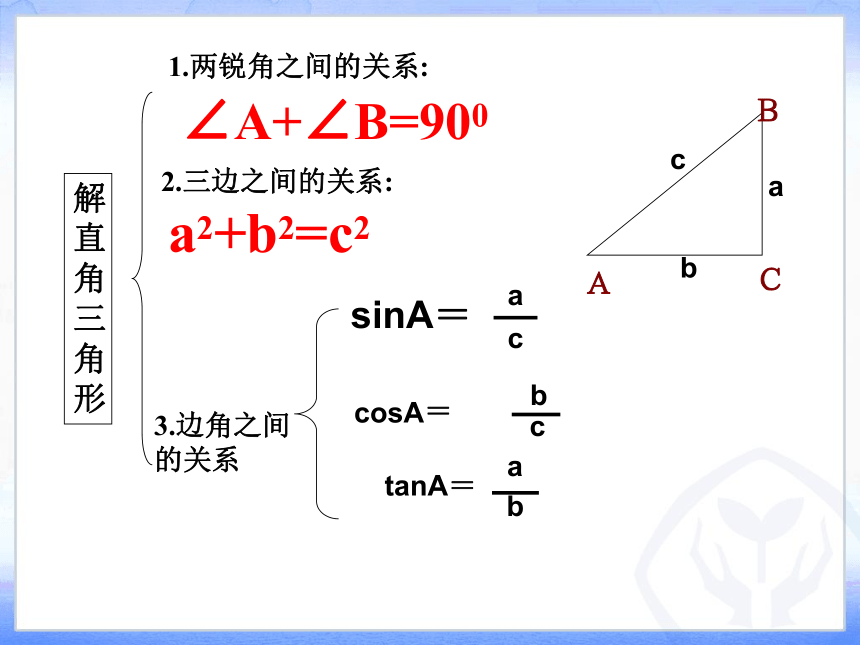
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=
a
c
cosA=
b
c
tanA=
a
b
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
i =
h
l
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
=tanα
问题2 整理一下本章所学的主要知识,你能发现它们之间的联系吗?你能画出一个本章的知识结构图吗?
直角三角形中的边角关系
锐角 三角函数
解直角三角形
实际问题
体系建构
题型1 三角函数
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
基础练习
4. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ABC=( )
,
A.
A.tan∠AED B.cot∠AED
C.sin∠AED D.cos∠AED
5. 如图所示,AB是⊙O的直
径,弦AC、BD相交于E,则
等于( )
6.计算:
|-
|+(cos60°-tan30°)+
.
A
D
题型2 解直角三角形
如图,在 Rt△ABC 中,∠C=90°,AB=10,
cos B= ,求 sin B,tan A 的值.
若去掉“AB=10”这一条件,你还能完成此题的解答吗?
C
A
10
B
题型3 解非直角三角形
1.如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).
2.如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?
1、解:过C作CD⊥AB于D,
设CD=x.在Rt△ACD中,tan60°=
在Rt△BCD中,BD=CD=x.
∴
x+x=8.
解得x=4(3-
).
=16(3-
)=48-16
.
∴AD=
x.
AB·CD=
×8×4(3-
∴S△ABC=
)
CD
AD
2.解:过P作PC⊥AB于C点,据题意知:
AB=9×
=3,∠PAB=90°-60°=30°,
∠PBC=90°-45°=45°,∠PCB=90°.
∴PC=BC.
在Rt△APC中,
PC>3.
∴客轮不改变方向继续前进无触礁危险.
tan30°=
,
即
=
,
1、解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2.(1)把实际问题转化成数学问题,这个转化为两 个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
方法小结
1、 一副直角三角板如图放置,点 C 在 FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A= 60°,AC=10,试求 CD 的长.
提高训练
2、 城市规划期间,欲拆除一电线杆 AB,已知距电线杆 AB 水平距离 14 m 的 D 处有一大坝,背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,在坝顶 C 处测得杆顶 A 的仰角为 30°,D,E 之间是宽为 2 m 的人行道.试问:在拆除电线杆 AB 时,为确保行人安全,是否需要将此人行道封上?
A
B
G
C
E D
F
30°
人行道
思考:如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
A
B
水平地面
C
O
山坡
60°
45°
P
E
锐角三角函数复习小结
复习目标: 1.复习本章的重点内容,整理本章知识,形成知识 体系; 2.熟练掌握直角三角形的解法,并用相关知识解决 一些简单的实际问题,进一步加深对锐角三角函 数的认识.
复习重点: 梳理本章的知识结构体系,并灵活运用锐角三角函数和解直角三角形的知识解决问题.
知识梳理
问题1 请同学们解答下列问题:
(1)我们已学过哪几种锐角三角函数?写出如图所示的直角三角形中两个锐角的三角函数.
C
A
B
知识梳理
问题1 请同学们解答下列问题:
(2)特殊角的三角形函数值是什么?
C
A
B
30°,45°,60°的三角函数值
30° 45° 60°
sina
cosa
tana
1
┌
┌
450
450
300
600
解直角三角形:(如图)
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
(3)已知哪两个条件可以解直角三角形?
你能根据不同的已知条件解直角三角形吗?
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
A
C
B
a
b
c
sinA=
a
c
cosA=
b
c
tanA=
a
b
在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
i =
h
l
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
=tanα
问题2 整理一下本章所学的主要知识,你能发现它们之间的联系吗?你能画出一个本章的知识结构图吗?
直角三角形中的边角关系
锐角 三角函数
解直角三角形
实际问题
体系建构
题型1 三角函数
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
基础练习
4. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ABC=( )
,
A.
A.tan∠AED B.cot∠AED
C.sin∠AED D.cos∠AED
5. 如图所示,AB是⊙O的直
径,弦AC、BD相交于E,则
等于( )
6.计算:
|-
|+(cos60°-tan30°)+
.
A
D
题型2 解直角三角形
如图,在 Rt△ABC 中,∠C=90°,AB=10,
cos B= ,求 sin B,tan A 的值.
若去掉“AB=10”这一条件,你还能完成此题的解答吗?
C
A
10
B
题型3 解非直角三角形
1.如图所示,已知:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC的面积(结果可保留根号).
2.如图,海上有一灯塔P,在它周围3海里处有暗礁,一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60°的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向,问客轮不改变方向继续前进有无触礁的危险?
1、解:过C作CD⊥AB于D,
设CD=x.在Rt△ACD中,tan60°=
在Rt△BCD中,BD=CD=x.
∴
x+x=8.
解得x=4(3-
).
=16(3-
)=48-16
.
∴AD=
x.
AB·CD=
×8×4(3-
∴S△ABC=
)
CD
AD
2.解:过P作PC⊥AB于C点,据题意知:
AB=9×
=3,∠PAB=90°-60°=30°,
∠PBC=90°-45°=45°,∠PCB=90°.
∴PC=BC.
在Rt△APC中,
PC>3.
∴客轮不改变方向继续前进无触礁危险.
tan30°=
,
即
=
,
1、解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
2.(1)把实际问题转化成数学问题,这个转化为两 个方面:一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.
(2)把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
方法小结
1、 一副直角三角板如图放置,点 C 在 FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A= 60°,AC=10,试求 CD 的长.
提高训练
2、 城市规划期间,欲拆除一电线杆 AB,已知距电线杆 AB 水平距离 14 m 的 D 处有一大坝,背水坡 CD的坡度 i =2∶1,坝高 CF 为 2 m,在坝顶 C 处测得杆顶 A 的仰角为 30°,D,E 之间是宽为 2 m 的人行道.试问:在拆除电线杆 AB 时,为确保行人安全,是否需要将此人行道封上?
A
B
G
C
E D
F
30°
人行道
思考:如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡
度为 ,(即tan∠PAB= )且O、A、B在同一
条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
A
B
水平地面
C
O
山坡
60°
45°
P
E
