人教版数学八年级下册19.3 课题学习 选择方案 课件(共38张PPT)
文档属性
| 名称 | 人教版数学八年级下册19.3 课题学习 选择方案 课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 22:11:16 | ||
图片预览









文档简介
(共38张PPT)
导入新课
讲授新课
当堂练习
课堂小结
19.3 课题学习 选择方案
第十九章 一次函数
情境引入
学习目标
1.会用一次函数知识解决方案选择问题,体会函数模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
导入新课
讲授新课
选择方案
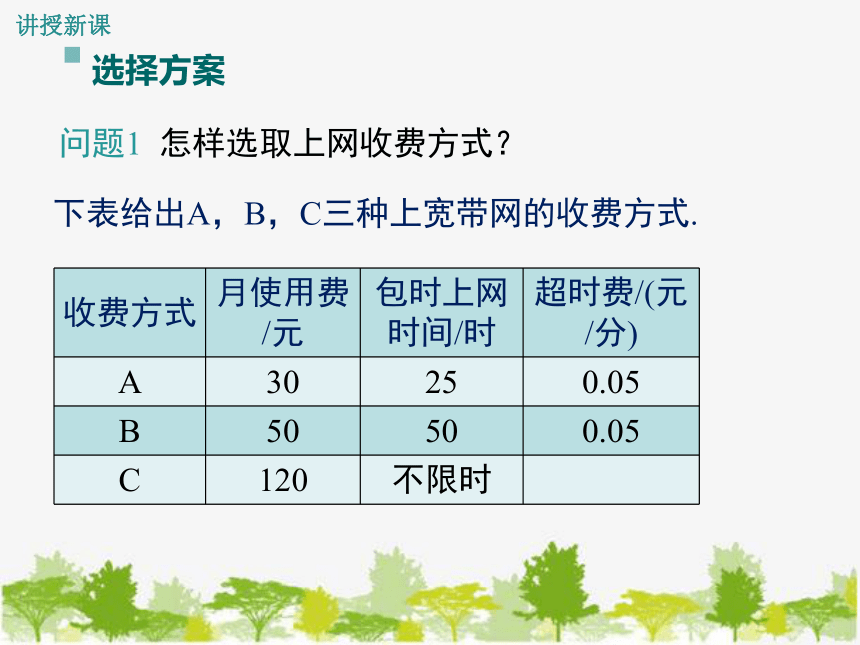
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
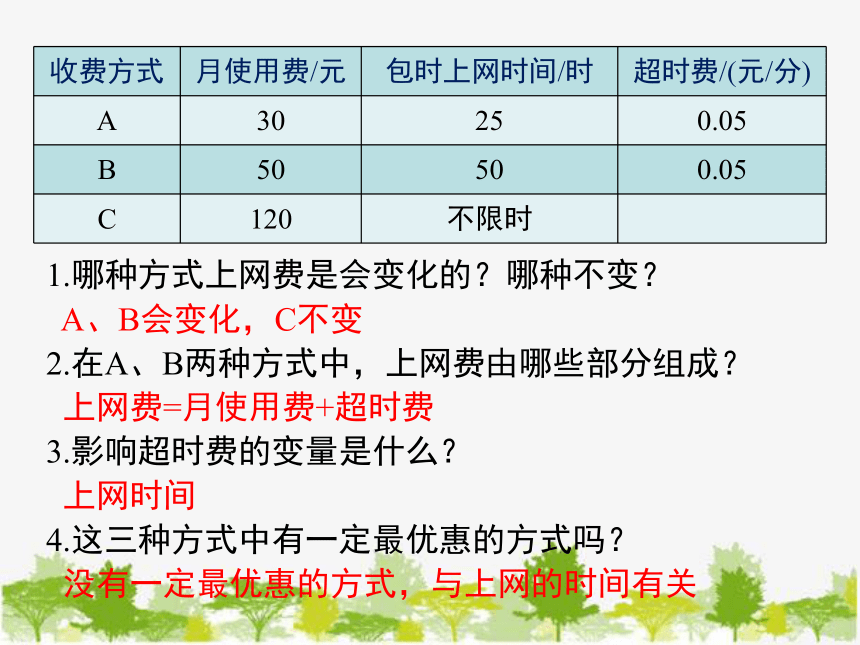
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
5.设月上网时间为x小时,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 的条件下,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
6.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
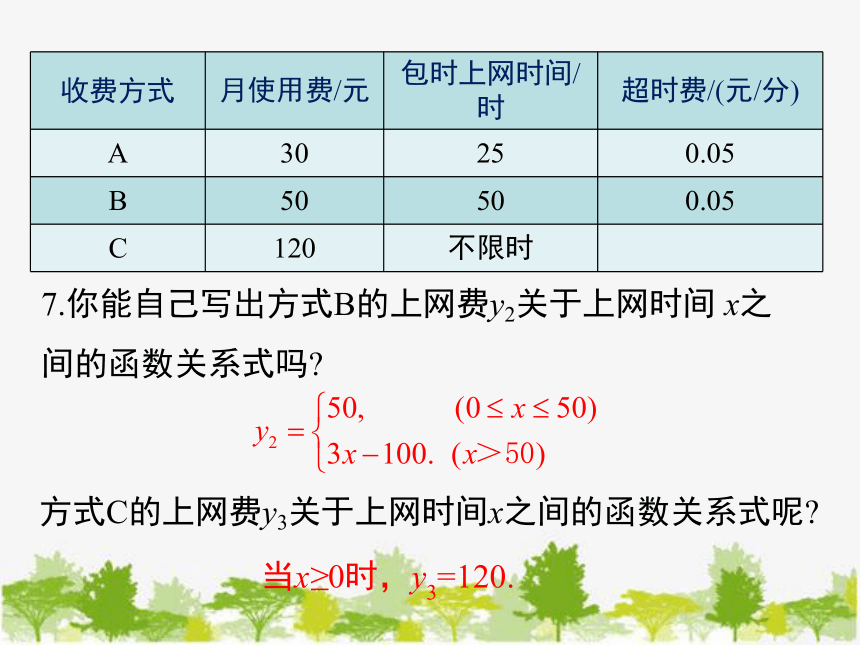
7.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
当上网时间__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(分钟)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出
哪种付费方式合算?
做一做
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分钟时,选择A或B方案费用一样;
当通话时间少于150分钟时,选择B方案费合算;
当通话时间多于150分钟时,选择A方案合算.
问题2 怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题1:租车的方案有哪几种?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题4:要使6名教师至少在每辆车上有一名,你能确定排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6辆,可以排除方案(2)——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分3种情况;
方法2:设租甲种车x辆,确定x的范围.
(1)为使240名师生有车坐,可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
除了分别计算两种方案的租金外,还有其他选择方案的方法吗?
由函数可知 y 随 x 增大而增大,所以 x = 4时 y 最小.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
总结归纳
例 某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1)该厂对这两种型号挖掘机有几种生产方案? (2)该厂如何生产获得最大利润? (3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
分析:可用信息:
①A、B两种型号的挖掘机共100台;
②所筹生产资金不少于22400万元,但不超过22500万元;
③所筹资金全部用于生产,两种型号的挖掘机可全部售出.
解:(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意知:
(1)该厂对这两种型号挖掘机有几种生产方案?
分析:设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意得不等式组 .
∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台, B型60台.
解得 37.5≤x≤40
∵x取正整数, ∴x为38、39、40
∴当x=38时,W最大=5620 (万元),
即生产A型38台,B型62台时,获得最大利润.
(2)该厂如何生产获得最大利润?
分析:利润与两种挖掘机的数量有关,因此可建立利润与挖掘机数量的函数关系式.
W=50x+60(100-x)
= -10x+6000
解:设获得利润为W(万元),由题意知:
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?
③当m>10时,取x=40,W最大, 即A型挖掘机生产40台,B型生产60台.
分析:在(2)的基础上,售价改变,则应重新建立利润与挖掘机数量的函数关系式,并注意讨论m的取值范围.
解:由题意知:W=(50+m)x+60(100-x)
= (m-10)x+6000
∴①当0<m<10时,取x=38,W最大 , 即A型挖掘机生产38台,B型挖掘机生产62台;
②当m=10时,m-10=0,三种生产获得利润相等;
做一做
抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
广兴
50车
中山
50车
江津
60车
白沙
40车
(50-x)
(60-x)
x
650
500
700
600
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60- x)+500(50 -x)+650(x-10)
y=50x+60500
(x-10)
由
得
∵ k=50>0 ,y随x的增大而增大,
∴当x=10时,y有最小值, y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
∴
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
当堂练习
2.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
3. 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x 元;选乙旅行社,应付(60x+1000)元.记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
观察图象,可知:当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50. 所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0), 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
课堂小结
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
导入新课
讲授新课
当堂练习
课堂小结
19.3 课题学习 选择方案
第十九章 一次函数
情境引入
学习目标
1.会用一次函数知识解决方案选择问题,体会函数模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
导入新课
讲授新课
选择方案
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
5.设月上网时间为x小时,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 的条件下,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
6.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
7.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
当上网时间__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费
为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话
时间t(分钟)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出
哪种付费方式合算?
做一做
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分钟时,选择A或B方案费用一样;
当通话时间少于150分钟时,选择B方案费合算;
当通话时间多于150分钟时,选择A方案合算.
问题2 怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题1:租车的方案有哪几种?
共三种:(1)单独租甲种车;(2)单独租乙种车;
(3)甲种车和乙种车都租.
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题2:如果单独租甲种车需要多少辆?乙种车呢?
问题3:如果甲、乙都租,你能确定合租车辆的范围吗?
汽车总数不能小于6辆,不能超过8辆.
单独租甲种车要6辆,单独租乙种车要8辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
问题4:要使6名教师至少在每辆车上有一名,你能确定排除哪种方案?你能确定租车的辆数吗?
说明了车辆总数不会超过6辆,可以排除方案(2)——单独租乙种车;所以租车的辆数只能为6辆.
问题5:在问题3中,合租甲、乙两种车的时候,又有很多种情况,面对这样的问题,我们怎样处理呢?
方法1:分类讨论——分3种情况;
方法2:设租甲种车x辆,确定x的范围.
(1)为使240名师生有车坐,可以确定x的一个范围吗?
(2)为使租车费用不超过2300元,又可以确定x的范围吗?
结合问题的实际意义,你能有几种不同的租车方案 为节省费用应选择其中的哪种方案?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
设租用 x 辆甲种客车,则租车费用y(单位:元)是 x 的函数,即
怎样确定 x 的取值范围呢
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
x 辆
(6-x)辆
除了分别计算两种方案的租金外,还有其他选择方案的方法吗?
由函数可知 y 随 x 增大而增大,所以 x = 4时 y 最小.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
总结归纳
例 某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1)该厂对这两种型号挖掘机有几种生产方案? (2)该厂如何生产获得最大利润? (3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
分析:可用信息:
①A、B两种型号的挖掘机共100台;
②所筹生产资金不少于22400万元,但不超过22500万元;
③所筹资金全部用于生产,两种型号的挖掘机可全部售出.
解:(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意知:
(1)该厂对这两种型号挖掘机有几种生产方案?
分析:设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意得不等式组 .
∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台, B型60台.
解得 37.5≤x≤40
∵x取正整数, ∴x为38、39、40
∴当x=38时,W最大=5620 (万元),
即生产A型38台,B型62台时,获得最大利润.
(2)该厂如何生产获得最大利润?
分析:利润与两种挖掘机的数量有关,因此可建立利润与挖掘机数量的函数关系式.
W=50x+60(100-x)
= -10x+6000
解:设获得利润为W(万元),由题意知:
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?
③当m>10时,取x=40,W最大, 即A型挖掘机生产40台,B型生产60台.
分析:在(2)的基础上,售价改变,则应重新建立利润与挖掘机数量的函数关系式,并注意讨论m的取值范围.
解:由题意知:W=(50+m)x+60(100-x)
= (m-10)x+6000
∴①当0<m<10时,取x=38,W最大 , 即A型挖掘机生产38台,B型挖掘机生产62台;
②当m=10时,m-10=0,三种生产获得利润相等;
做一做
抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
广兴
50车
中山
50车
江津
60车
白沙
40车
(50-x)
(60-x)
x
650
500
700
600
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60- x)+500(50 -x)+650(x-10)
y=50x+60500
(x-10)
由
得
∵ k=50>0 ,y随x的增大而增大,
∴当x=10时,y有最小值, y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
∴
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
当堂练习
2.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
①②③
3. 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x 元;选乙旅行社,应付(60x+1000)元.记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
观察图象,可知:当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49人时,选择甲旅行社费用较少;
当人数为51~100人时,选择乙旅行社费用较少.
x/人
50
60
y/元
800
1600
3200
2400
4000
4800
5600
O
10
20
30
40
70
80
90
y1= 80x
y2= 60x+1000
解法二:
(1)当y1=y2,即80x= 60x+1000时,x=50.
所以当人数为50时,选择甲或乙旅行社费用都一样;
(2)当y1 > y2,即80x > 60x+1000时, 得x > 50. 所以当人数为51~100人时 ,选择乙旅行社费用较少;
(3)当y1 < y2,即80x < 60x+1000时,得x<50.
所以当人数为0~49人时,选择甲旅行社费用较少;
解法三:设选择甲、乙旅行社费用之差为y,
则y=y1-y2=80x-(60x+1000)=20x-1000.
画出一次函数y= 20x-1000的图象如下图.
O
20
40
60
-200
-400
-600
-800
-1000
y
x
y= 20x-1000
它与x轴交点为(50,0), 由图可知:
(1)当x=50时,y=0,即y1=y2;
(2)当x>50时,y > 0,即y1 > y2;
(3)当x<50时,y <0,即y1 < y2.
课堂小结
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
