9.2.1 总体取值规律的估计 课件(共29张PPT)
文档属性
| 名称 | 9.2.1 总体取值规律的估计 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 942.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
2021-2022学年人教A版必修二高一数学课件★★
第9章 统计
9.2 用样本估计总体
9.2.1 总体取值规律的估计
1
频率分布直方图
探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a, 用水量不超过a的部分按平价收费,超过a的部分按议价收费.
如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
如果标准定的太低,会影响很多居民的日常生活;如果标准太高,则不利于节水。为了确定一个较为合理的用水标准,必须先了解在全市所有居民用户中,月用水量在不同范围内的居民用户所占的比例情况。
通常采用抽样调查的方式,通过分析样本观测数据,来估计全市居民用户月均用水量的分布情况。
1
频率分布直方图
假设通过抽样,我们获得了100位居民某年的月均用水量(单位: t):
这些数字能告诉我们什么呢?
在这个问题中,总体是该市的全体居民用户,个体是每户居民,调查变量是居民用户的月均用水量。
问题1:在这个问题中,总体、个体、调查变量分别是什么?
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
1
频率分布直方图
如果将这组数据按从小到大排序,发现这组数据的最小值是1.3t, 最大值是28.0t,其他在1.3t和28.0t之间。为了更深入地挖掘数据蕴含的信息,需要对数据作进一步的整理与分析。
在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数。
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民占全市居民用户的比例,所以选择频率分布表和频率分布直方图在整理和表示数据。
问题2:从这组数据我们能发现什么信息呢?
1
频率分布直方图
频数:在总体(或样本)中,某个个体出现的次数叫做这个个体的频数。
频率:某个个体的频数与总体(或样本)中所含个体的数量的比叫做这个个体的频率。
问题3:什么是频数?什么是频率?
问题4:什么是样本的频率分布及频率分布表
频率分布:根据随机抽取的样本量的大小,分别计算某一事件出现的频率,这些频率的分布规律就叫做样本的频率分布.
频率分布表:为了能直观的显示样本的频率分布情况,通常将样本量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,这张表叫做频率分布表.
1
频率分布直方图
问题5:什么样本的频率分布直方图?
频率分布直方图:为了将频率分布表中的结果直观形象地表现出来,常画出频率分布直方图. 画图时应以横轴表示分组,纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,画成小长方形,这样得到的直方图就是频率分布直方图.
问题6:画频数分布直方图的一般步骤是什么?
①计算最大值与最小值的差
②决定组距和组数
③将数据分组
④列频数分布表
⑤画频数分布直方图
1
频率分布直方图
1.求极差(即计算最大值与最小值的差)
2.决定组距和组数
3.将数据分组
组数=
极差
组距
= = 8.9
26.7
3
[1.2,4.2),[4.2,7.2),[7.2,10.2),…,[25.2,28.2]
组数为9
28.0 -1.3=26.7
取组距为3
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组.
当样本容量不超过 100 时,常分成 5~12组.
由于组距为3,9 个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值
在制作频率分布表、画频率分布直方图之前,我们先按以下步骤画频数分布直方图。
1
频率分布直方图
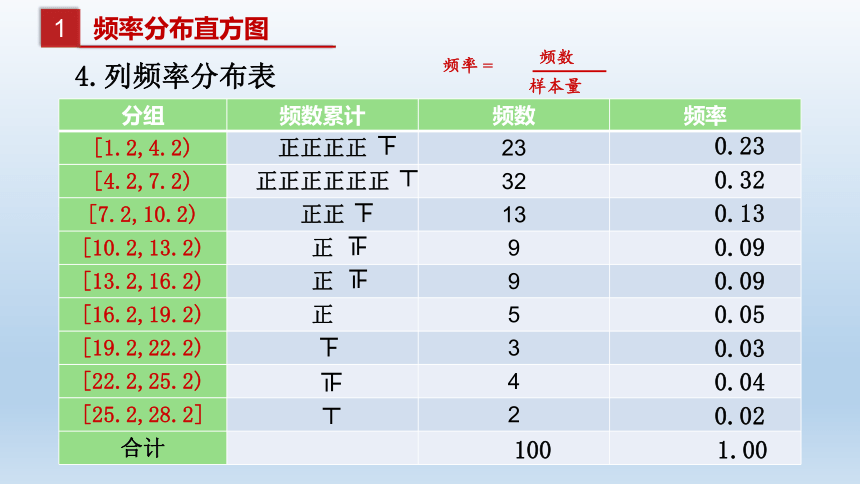
分组 频数累计 频数 频率
[1.2,4.2) 正正正正 23
[4.2,7.2) 正正正正正正 32
[7.2,10.2) 正正 13
[10.2,13.2) 正 9
[13.2,16.2) 正 9
[16.2,19.2) 正 5
[19.2,22.2) 3
[22.2,25.2) 4
[25.2,28.2] 2
合计
100
0.32
0.13
0.09
0.09
0.05
0.03
0.04
0.02
1.00
0.23
4.列频率分布表
频率 =
频数
样本量
1
频率分布直方图
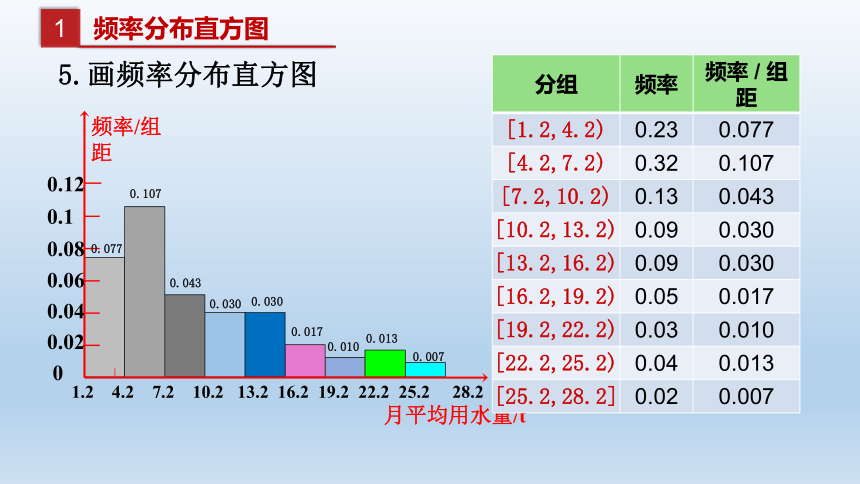
5.画频率分布直方图
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
分组 频率 频率 / 组距
[1.2,4.2) 0.23 0.077
[4.2,7.2) 0.32 0.107
[7.2,10.2) 0.13 0.043
[10.2,13.2) 0.09 0.030
[13.2,16.2) 0.09 0.030
[16.2,19.2) 0.05 0.017
[19.2,22.2) 0.03 0.010
[22.2,25.2) 0.04 0.013
[25.2,28.2] 0.02 0.007
1
频率分布直方图
思考:频率分布直方图中各小长方形的面积表示什么?各小长方形的面积总和为多少?
小长方形的面积=
组距X
组距
频率
=频率
所以各小长方形的面积表示相应各组的频率.
各小长方形的面积总和为1.
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
1
频率分布直方图
1. 求极差:即数据中最大值与最小值的差;
2. 决定组距和组数:组数=极差/组距;
注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“取整”;③当样本容量不超过100时,按照数据的多少,通常分成5~12组.
3. 将数据分组:通常对组内数值所在区间,取左闭右开区间 , 最后一组取闭区间;
4. 登记频数, 计算频率和频率/组距 , 列频率分布表:
一般分四列:分组、频数累计、频数、频率,最后一行是合计.其中频率合计应是样本容量,频率合计是1.
5. 画频率分布直方图:
画图时,应以横轴表示分组,纵轴表示频率/组距.其相应组距上的频率等于该组上的小长方形的面积.
思考:画频率分布直方图有哪几个步骤?
1
频率分布直方图
【例1】 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50, 60),3;[60, 70), 10;[70, 80), 15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例.
1
频率分布直方图
解 (1)频率分布表如下:
成绩分组 频数 频率 累积频率
[40,50) 2 0.04 0.04
[50,60) 3 0.06 0.1
[60,70) 10 0.2 0.3
[70,80) 15 0.3 0.6
[80,90) 12 0.24 0.84
[90,100] 8 0.16 1.00
合计 50 1.00
1
频率分布直方图
(2)频率分布直方图如图所示.
(3)学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,所以估计成绩在[60,90)分的学生比例为74%.
1
频率分布直方图
【例2】 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率约是多少?
1
频率分布直方图
1
频率分布直方图
跟踪训练1. 某校100名学生期中考试语文成绩(单位:分)的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)若这100名学生的语文成绩在某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 [50,60) [60,70) [70,80) [80,90)
x∶y 1∶1 2∶1 3∶4 4∶5
1
频率分布直方图
解 (1)依题意得,10×(2a+0.02+0.03+0.04)=1,解得a=0.005.
2
统计图表
用单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来,这样的统计图称为条形统计图.
优点:条形统计图不但可以直观的反映数据分布的大致情况,
还可以清晰地表示出各个区间的具体数目,易于比较
数据间的差别.
缺点:会损失数据的部分信息,且不能明确显示部分与整体
的关系.
1. 条形统计图
2
统计图表
建立直角坐标系,用横轴上的数字表示样本值,用纵轴上的单位长度表示一定的数量,根据样本值和数量的多少描出相应点,然后用直线段顺次连接相应点,得到一条折线,用这条折线.表示样本数据情况,这种表达和分析数据的统计图叫做折线统计图.
折线统计图可以通过连接条形统计图各个直条上边的中点顺次连接而得到
2. 折线统计图
2
统计图表
缺点:折线统计图不能直观反映数据的分布情况,且不适合总体分布较多的情况
优点:折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地表示数量的增减变化情况.
2. 折线统计图
2
统计图表
扇形统计图中用整个圆面积代表总体,圆内的各个扇形分别代表总体中的不同部分,扇形面积的大小反映所表示的那部分占总体的百分比的大小.
优点:扇形统计图可以很清楚的表示各部分与总体之间的关系,即扇形统计图能清楚地表示出各部分在总体中所
占的百分比
缺点:会损失数据的部分信息,且不能明确显示部分与整体的关系.
3. 扇形统计图
2
统计图表
角度1 条形统计图
【例1】 为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如图所示.
请根据统计图提供的信息回答以下问题:
(1)求抽取的学生数;
(2)若该校有3 000名学生,估计喜欢收听易中天《品三国》的学生人数;
(3)估计该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的百分比
2
统计图表
解 (1)从统计图上可以看出,
喜欢收听于丹析《庄子》的男生有20人,女生有10人;
喜欢收听《故宫博物院》的男生有30人,女生有15人;
喜欢收听于丹析《论语》的男生有30人,女生有38人;
喜欢收听易中天《品三国》的男生有64人,女生有42人;
喜欢收听刘心武评《红楼梦》的男生有6人,女生有45人.
所以抽取的学生数为20+10+30+15+30+38+64+42+6+45=300(人).
2
统计图表
角度2 折线统计图
【例2】 小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么时间出院?
2
统计图表
解 (1)根据横轴表示的意义,可知护士每6小时给小明测量一次体温.
(2)从折线统计图中的最高点和最低点对应的纵轴意义,可知最高体温是39.5摄氏度,最低体温是36.8摄氏度.
(3)从图中可知小明的体温已经下降,并趋于稳定,因此病情在好转.
(4)9月8日18时小明的体温是37摄氏度,其后的体温未超过37.2摄氏度,自9月8日18时起计算,连续36小时后对应的时间为9月10日凌晨6时,因此小明最快可以在9月10凌晨6时出院.
2
统计图表
角度3 扇形统计图
【例3】 下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图:
(1)从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
解 (1)不能.因为两所学校收到艺术作品的总数不知道.
2
统计图表
跟踪训练1 如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250 B.150
C.400 D.300
答案 A
跟踪训练2 .200辆汽车经过某一雷达地区,时速的频率分布直方图如图所示,则时速超过60 km/h(含60 km/h)的汽车数量为( )
A.65辆 B.76辆
C.88辆 D.95辆
解析 由频率分布直方图可得数据落在[60,80)内
的频率是(0.028+0.010)×10=0.38,故时速超过60 km/h
(含60 km/h)的汽车数量为200×0.38=76(辆).
答案 B
2
统计图表
2021-2022学年人教A版必修二高一数学课件★★
第9章 统计
9.2 用样本估计总体
9.2.1 总体取值规律的估计
1
频率分布直方图
探究:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a, 用水量不超过a的部分按平价收费,超过a的部分按议价收费.
如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
如果标准定的太低,会影响很多居民的日常生活;如果标准太高,则不利于节水。为了确定一个较为合理的用水标准,必须先了解在全市所有居民用户中,月用水量在不同范围内的居民用户所占的比例情况。
通常采用抽样调查的方式,通过分析样本观测数据,来估计全市居民用户月均用水量的分布情况。
1
频率分布直方图
假设通过抽样,我们获得了100位居民某年的月均用水量(单位: t):
这些数字能告诉我们什么呢?
在这个问题中,总体是该市的全体居民用户,个体是每户居民,调查变量是居民用户的月均用水量。
问题1:在这个问题中,总体、个体、调查变量分别是什么?
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.4 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
1
频率分布直方图
如果将这组数据按从小到大排序,发现这组数据的最小值是1.3t, 最大值是28.0t,其他在1.3t和28.0t之间。为了更深入地挖掘数据蕴含的信息,需要对数据作进一步的整理与分析。
在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数。
在这个实际问题中,因为我们更关心月均用水量在不同范围内的居民占全市居民用户的比例,所以选择频率分布表和频率分布直方图在整理和表示数据。
问题2:从这组数据我们能发现什么信息呢?
1
频率分布直方图
频数:在总体(或样本)中,某个个体出现的次数叫做这个个体的频数。
频率:某个个体的频数与总体(或样本)中所含个体的数量的比叫做这个个体的频率。
问题3:什么是频数?什么是频率?
问题4:什么是样本的频率分布及频率分布表
频率分布:根据随机抽取的样本量的大小,分别计算某一事件出现的频率,这些频率的分布规律就叫做样本的频率分布.
频率分布表:为了能直观的显示样本的频率分布情况,通常将样本量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,这张表叫做频率分布表.
1
频率分布直方图
问题5:什么样本的频率分布直方图?
频率分布直方图:为了将频率分布表中的结果直观形象地表现出来,常画出频率分布直方图. 画图时应以横轴表示分组,纵轴表示各组频率与组距的比值,以各个组距为底,以各频率除以组距的商为高,画成小长方形,这样得到的直方图就是频率分布直方图.
问题6:画频数分布直方图的一般步骤是什么?
①计算最大值与最小值的差
②决定组距和组数
③将数据分组
④列频数分布表
⑤画频数分布直方图
1
频率分布直方图
1.求极差(即计算最大值与最小值的差)
2.决定组距和组数
3.将数据分组
组数=
极差
组距
= = 8.9
26.7
3
[1.2,4.2),[4.2,7.2),[7.2,10.2),…,[25.2,28.2]
组数为9
28.0 -1.3=26.7
取组距为3
组距:指每个小组的两个端点的距离,
组数:将数据分组,当数据在100个以内时,
按数据多少常分5-12组.
当样本容量不超过 100 时,常分成 5~12组.
由于组距为3,9 个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值
在制作频率分布表、画频率分布直方图之前,我们先按以下步骤画频数分布直方图。
1
频率分布直方图
分组 频数累计 频数 频率
[1.2,4.2) 正正正正 23
[4.2,7.2) 正正正正正正 32
[7.2,10.2) 正正 13
[10.2,13.2) 正 9
[13.2,16.2) 正 9
[16.2,19.2) 正 5
[19.2,22.2) 3
[22.2,25.2) 4
[25.2,28.2] 2
合计
100
0.32
0.13
0.09
0.09
0.05
0.03
0.04
0.02
1.00
0.23
4.列频率分布表
频率 =
频数
样本量
1
频率分布直方图
5.画频率分布直方图
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
分组 频率 频率 / 组距
[1.2,4.2) 0.23 0.077
[4.2,7.2) 0.32 0.107
[7.2,10.2) 0.13 0.043
[10.2,13.2) 0.09 0.030
[13.2,16.2) 0.09 0.030
[16.2,19.2) 0.05 0.017
[19.2,22.2) 0.03 0.010
[22.2,25.2) 0.04 0.013
[25.2,28.2] 0.02 0.007
1
频率分布直方图
思考:频率分布直方图中各小长方形的面积表示什么?各小长方形的面积总和为多少?
小长方形的面积=
组距X
组距
频率
=频率
所以各小长方形的面积表示相应各组的频率.
各小长方形的面积总和为1.
月平均用水量/t
0.12
0.1
0.08
0.06
0.04
0.02
0
1.2 4.2 7.2 10.2 13.2 16.2 19.2 22.2 25.2 28.2
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0.077
频率/组距
1
频率分布直方图
1. 求极差:即数据中最大值与最小值的差;
2. 决定组距和组数:组数=极差/组距;
注意:①一般样本容量越大,所分组数越多;②为方便起见,组距的选择应力求“取整”;③当样本容量不超过100时,按照数据的多少,通常分成5~12组.
3. 将数据分组:通常对组内数值所在区间,取左闭右开区间 , 最后一组取闭区间;
4. 登记频数, 计算频率和频率/组距 , 列频率分布表:
一般分四列:分组、频数累计、频数、频率,最后一行是合计.其中频率合计应是样本容量,频率合计是1.
5. 画频率分布直方图:
画图时,应以横轴表示分组,纵轴表示频率/组距.其相应组距上的频率等于该组上的小长方形的面积.
思考:画频率分布直方图有哪几个步骤?
1
频率分布直方图
【例1】 从某校高三学生中抽取50名参加数学竞赛,成绩分组(单位:分)及各组的频数如下:
[40,50),2;[50, 60),3;[60, 70), 10;[70, 80), 15;[80,90),12;[90,100],8.
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例.
1
频率分布直方图
解 (1)频率分布表如下:
成绩分组 频数 频率 累积频率
[40,50) 2 0.04 0.04
[50,60) 3 0.06 0.1
[60,70) 10 0.2 0.3
[70,80) 15 0.3 0.6
[80,90) 12 0.24 0.84
[90,100] 8 0.16 1.00
合计 50 1.00
1
频率分布直方图
(2)频率分布直方图如图所示.
(3)学生成绩在[60,90)分的频率为0.2+0.3+0.24=0.74=74%,所以估计成绩在[60,90)分的学生比例为74%.
1
频率分布直方图
【例2】 为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小矩形的面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率约是多少?
1
频率分布直方图
1
频率分布直方图
跟踪训练1. 某校100名学生期中考试语文成绩(单位:分)的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)若这100名学生的语文成绩在某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 [50,60) [60,70) [70,80) [80,90)
x∶y 1∶1 2∶1 3∶4 4∶5
1
频率分布直方图
解 (1)依题意得,10×(2a+0.02+0.03+0.04)=1,解得a=0.005.
2
统计图表
用单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按照一定的顺序排列起来,这样的统计图称为条形统计图.
优点:条形统计图不但可以直观的反映数据分布的大致情况,
还可以清晰地表示出各个区间的具体数目,易于比较
数据间的差别.
缺点:会损失数据的部分信息,且不能明确显示部分与整体
的关系.
1. 条形统计图
2
统计图表
建立直角坐标系,用横轴上的数字表示样本值,用纵轴上的单位长度表示一定的数量,根据样本值和数量的多少描出相应点,然后用直线段顺次连接相应点,得到一条折线,用这条折线.表示样本数据情况,这种表达和分析数据的统计图叫做折线统计图.
折线统计图可以通过连接条形统计图各个直条上边的中点顺次连接而得到
2. 折线统计图
2
统计图表
缺点:折线统计图不能直观反映数据的分布情况,且不适合总体分布较多的情况
优点:折线统计图不但可以表示数量的多少,还可以通过折线的起伏清楚直观地表示数量的增减变化情况.
2. 折线统计图
2
统计图表
扇形统计图中用整个圆面积代表总体,圆内的各个扇形分别代表总体中的不同部分,扇形面积的大小反映所表示的那部分占总体的百分比的大小.
优点:扇形统计图可以很清楚的表示各部分与总体之间的关系,即扇形统计图能清楚地表示出各部分在总体中所
占的百分比
缺点:会损失数据的部分信息,且不能明确显示部分与整体的关系.
3. 扇形统计图
2
统计图表
角度1 条形统计图
【例1】 为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如图所示.
请根据统计图提供的信息回答以下问题:
(1)求抽取的学生数;
(2)若该校有3 000名学生,估计喜欢收听易中天《品三国》的学生人数;
(3)估计该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的百分比
2
统计图表
解 (1)从统计图上可以看出,
喜欢收听于丹析《庄子》的男生有20人,女生有10人;
喜欢收听《故宫博物院》的男生有30人,女生有15人;
喜欢收听于丹析《论语》的男生有30人,女生有38人;
喜欢收听易中天《品三国》的男生有64人,女生有42人;
喜欢收听刘心武评《红楼梦》的男生有6人,女生有45人.
所以抽取的学生数为20+10+30+15+30+38+64+42+6+45=300(人).
2
统计图表
角度2 折线统计图
【例2】 小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么时间出院?
2
统计图表
解 (1)根据横轴表示的意义,可知护士每6小时给小明测量一次体温.
(2)从折线统计图中的最高点和最低点对应的纵轴意义,可知最高体温是39.5摄氏度,最低体温是36.8摄氏度.
(3)从图中可知小明的体温已经下降,并趋于稳定,因此病情在好转.
(4)9月8日18时小明的体温是37摄氏度,其后的体温未超过37.2摄氏度,自9月8日18时起计算,连续36小时后对应的时间为9月10日凌晨6时,因此小明最快可以在9月10凌晨6时出院.
2
统计图表
角度3 扇形统计图
【例3】 下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图:
(1)从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
解 (1)不能.因为两所学校收到艺术作品的总数不知道.
2
统计图表
跟踪训练1 如图是甲、乙、丙、丁四组人数的扇形统计图的部分结果,根据扇形统计图的情况可以知道丙、丁两组人数和为( )
A.250 B.150
C.400 D.300
答案 A
跟踪训练2 .200辆汽车经过某一雷达地区,时速的频率分布直方图如图所示,则时速超过60 km/h(含60 km/h)的汽车数量为( )
A.65辆 B.76辆
C.88辆 D.95辆
解析 由频率分布直方图可得数据落在[60,80)内
的频率是(0.028+0.010)×10=0.38,故时速超过60 km/h
(含60 km/h)的汽车数量为200×0.38=76(辆).
答案 B
2
统计图表
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
