第九章 统计章节复习 课件(共31张PPT)
文档属性
| 名称 | 第九章 统计章节复习 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 759.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 11:43:42 | ||
图片预览









文档简介
(共31张PPT)
2021-2022学年人教A版必修二高一数学课件★★
第九章 统计
章节复习
1
知识体系
适用于
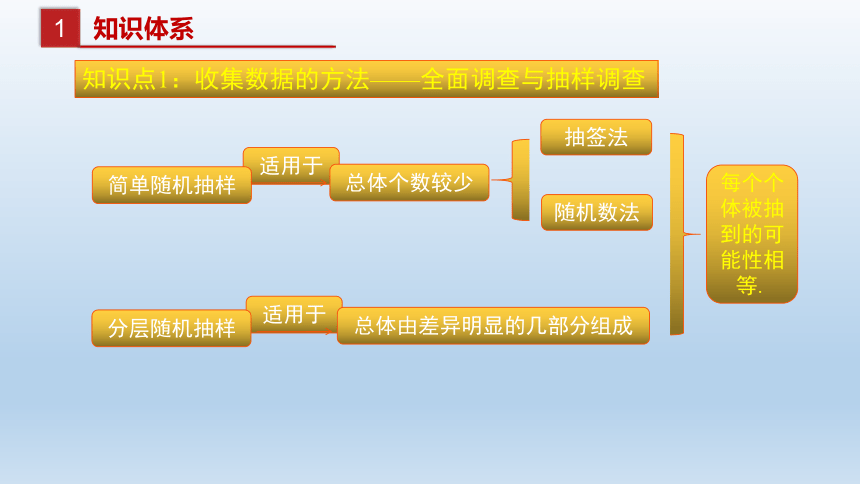
知识点1:收集数据的方法——全面调查与抽样调查
简单随机抽样
总体个数较少
抽签法
随机数法
适用于
分层随机抽样
总体由差异明显的几部分组成
每个个体被抽到的可能性相等.
1
知识体系
一、随机抽样
1.简单随机抽样
(1)特征:①逐个不放回的抽取;②每个个体被抽到的概率都相等.
(2)常用方法:①抽签法;②随机数法.
1
知识体系
1
知识体系
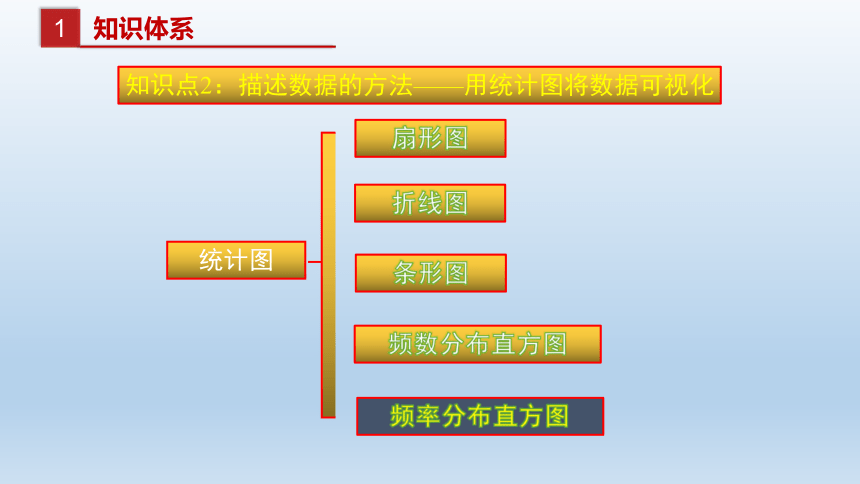
知识点2:描述数据的方法——用统计图将数据可视化
统计图
扇形图
折线图
条形图
频率分布直方图
频数分布直方图
1
知识体系
二、用样本估计总体
1.频率分布直方图
1
知识体系
知识点3:分析数据的方法——总体百分位数的估计
计算一组n个数据的第p百分位数的步骤:
(2)计算i=n×p%.
定义:一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(1)按从小到大排列原始数据.
(3)若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
1
知识体系
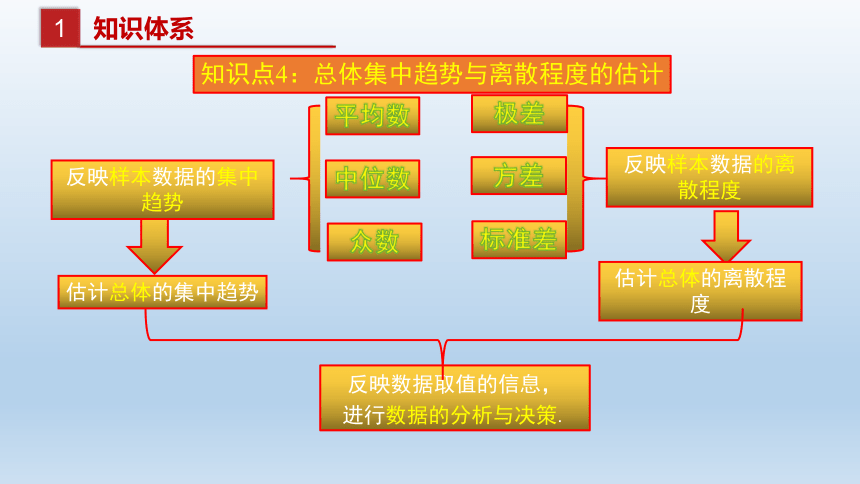
知识点4:总体集中趋势与离散程度的估计
反映数据取值的信息,
进行数据的分析与决策.
估计总体的集中趋势
平均数
众数
反映样本数据的集中趋势
中位数
反映样本数据的离散程度
极差
方差
标准差
估计总体的离散程度
1
知识体系
4.众数、中位数和平均数与总体集中趋势的估计
4.总体集中趋势的估计
1
知识体系
2
题型讲解
题型一:抽样方法
解析 问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法.
问题②中总体的个数较少,故可采用简单随机抽样.
答案 B
例1.①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样. 则问题与方法配对正确的是( ).
(A)①(1),②(2) (B)①(2),②(1)
(C)① (1),②(1) (D)①(2),②(2)
2
题型讲解
解析 因为各层抽样比相等,
答案 D
均为
即各层的人数分别是
例2.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层随机抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( ).
(A)12,24,15,9 (B)9,12,12,7
(C)8,15,12,5 (D)8,16,10,6
2
题型讲解
例3、假设要抽查某种品牌的850颗种子的发芽率,抽取60颗进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第2列的数3开始向右读,请你依次写出最先检测的4颗种子的编号________.(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
2
题型讲解
[解析] 第8行第2列的数3开始向右读第一个小于850的数字是301,
第二个数字是637,也符合题意,
第三个数字是859,大于850,舍去,
第四个数字是169,符合题意,
第五个数字是555,符合题意,
故答案为:301,637,169,555.
2
题型讲解
【对点练习】(1) 一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层随机抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
A.12,24,15,9 B.9,12,12,7
C.8,15,12,5 D.8,16,10,6
D
2
题型讲解
C
2
题型讲解
025,016,105,185,395
2
题型讲解
与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可利用频率和等于1求解.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.
题型二 用样本的取值规律估计总体的取值规律
2
题型讲解
例1、下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
2
题型讲解
[解析] (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
2
题型讲解
2
题型讲解
【对点练习】某电子商务公司对10 000名网络购物者2018年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,
消费金额在区间[0.5,0.9]内的
购物者的人数为________.
3
6 000
2
题型讲解
题型三 总体百分位数的估计
例1.某产品售后服务中心随机选取了10个工作日,分别记录了每个工作日接到的客户服务电话的数量(单位:次):
63 38 25 42 56 48 53 39 28 47
则上述数据的第50百分位数为________.
解析 把这组数据从小到大排序:25,28,38,39,42,47,48,53,56,63,
根据i=n×p%,计算得:i=10×50%=5.
因为i为整数,所以第p百分位数为第i项与第(i+1)项数据的平均数,即
2
题型讲解
例2.欧洲联盟委员会和荷兰环境评估署公布了2013年全球主要20个国家和地区的人均二氧化碳排放量,结果如下表:
国家和地区 人均排放 量/吨 国家和地区 人均排放 量/吨 国家和地区 人均排放
量/吨
中国 7.4 沙特阿拉伯 16.6 印度 1.7
美国 16.6 巴西 2.0 俄罗斯 12.6
欧盟 7.3 英国 7.5 日本 10.7
加拿大 15.7 墨西哥 3.9 德国 10.2
印度尼西亚 2.6 伊朗 5.3 韩国 12.7
意大利 6.4 澳大利亚 16.9 南非 6.2
法国 5.7 波兰 8.5
请计算这20个国家和地区的人均二氧化碳排放量的四分位数.
2
题型讲解
解:把这20个国家和地区的人均二氧化碳排放量按从小到大的顺序排列:1.7,2.0,2.6,3.9,5.3,5.7,6.2,6.4,7.3,7.4,7.5,8.5,10.2,10.7,12.6,12.7,15.7,16.6,16.6,16.9.
根据i=n×p%,计算得:i=20×25%=5.
因为i为整数,所以第p百分位数为第i项与第(i+1)项数据的平均数,即
第25百分位数为
同理可得,20×50%=10,所以这20个数的第50百分位数为
20×75%=15,所以这20个数的第75百分位数为
所以这20个国家和地区的人均二氧化碳排放量的四分位数为5.5,7.45,12.65.
2
题型讲解
例1.若样本x1,x2,x3,…,xn的平均数为7,方差为6,则对于3x1+1,3x2+1,3x3+1,…,3xn+1,下列结论正确的是( ).
(A)平均数是21,方差是6 (B)平均数是7,方差是54
(C)平均数是22,方差是6 (D)平均数是22,方差是54
如果数据x1 ,x2 ,… ,xn的平均数为 ,方差为s2,
则新数据ax1+b,ax2+b,… ,axn+b的平均数为 ,方差为 .
计算可得:
答案 D
题型四:数据的集中趋势和离散程度的估计
2
题型讲解
例2.某公司销售部有销售人员15人,为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
(1)求这15位销售人员该月销售量的平均数、中位数及众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额.
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
2
题型讲解
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
解 (1)根据平均数公式 ,计算可得:
因为数据出现次数最多的为210,所以众数也为210.
(3)我认为不合理.因为15人中有13人的销售额达不到320件.虽然320是这一组数据的平均数,但它却不能反映销售人员的一般水平.
根据题意,数据已由大到小排序,因为共15个数据,所以中位数为最中间的第7个数据,即210.
销售额应定为210件.这是由于210既是中位数,又是众数,是绝大部分人都能达到的销售额.
(2)
2
题型讲解
例3.甲、乙两位学生参加声乐大赛,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
现要从中选派一人参加声乐大赛,请你计算出平均成绩和方差,并分析选派哪位学生参加合适?
2
题型讲解
解 根据平均数公式 ,可得甲、乙两人成绩的平均数:
根据方差的计算公式, 可得甲、乙两名
学生成绩的方差分别为:
2
题型讲解
方差刻画了数据的离散程度或波动幅度.
方差越大,数据的离散程度越大,越不稳定.
方差越小,数据的离散程度越小,越稳定.
平均数反映了数据的集中趋势.
平均数 方差
甲 85 35.5
乙 85 41
所以甲的成绩较稳定,应派甲参赛.
2021-2022学年人教A版必修二高一数学课件★★
第九章 统计
章节复习
1
知识体系
适用于
知识点1:收集数据的方法——全面调查与抽样调查
简单随机抽样
总体个数较少
抽签法
随机数法
适用于
分层随机抽样
总体由差异明显的几部分组成
每个个体被抽到的可能性相等.
1
知识体系
一、随机抽样
1.简单随机抽样
(1)特征:①逐个不放回的抽取;②每个个体被抽到的概率都相等.
(2)常用方法:①抽签法;②随机数法.
1
知识体系
1
知识体系
知识点2:描述数据的方法——用统计图将数据可视化
统计图
扇形图
折线图
条形图
频率分布直方图
频数分布直方图
1
知识体系
二、用样本估计总体
1.频率分布直方图
1
知识体系
知识点3:分析数据的方法——总体百分位数的估计
计算一组n个数据的第p百分位数的步骤:
(2)计算i=n×p%.
定义:一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(1)按从小到大排列原始数据.
(3)若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;
若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
1
知识体系
知识点4:总体集中趋势与离散程度的估计
反映数据取值的信息,
进行数据的分析与决策.
估计总体的集中趋势
平均数
众数
反映样本数据的集中趋势
中位数
反映样本数据的离散程度
极差
方差
标准差
估计总体的离散程度
1
知识体系
4.众数、中位数和平均数与总体集中趋势的估计
4.总体集中趋势的估计
1
知识体系
2
题型讲解
题型一:抽样方法
解析 问题①中的总体是由差异明显的几部分组成的,故可采用分层随机抽样方法.
问题②中总体的个数较少,故可采用简单随机抽样.
答案 B
例1.①某小区有800户家庭,其中高收入家庭200户,中等收入家庭480户,低收入家庭120户,为了了解有关家用轿车购买力的某个指标,要从中抽取一个容量为100的样本;②从10名学生中抽取3人参加座谈会.方法:(1)简单随机抽样;(2)分层随机抽样. 则问题与方法配对正确的是( ).
(A)①(1),②(2) (B)①(2),②(1)
(C)① (1),②(1) (D)①(2),②(2)
2
题型讲解
解析 因为各层抽样比相等,
答案 D
均为
即各层的人数分别是
例2.一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层随机抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( ).
(A)12,24,15,9 (B)9,12,12,7
(C)8,15,12,5 (D)8,16,10,6
2
题型讲解
例3、假设要抽查某种品牌的850颗种子的发芽率,抽取60颗进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第2列的数3开始向右读,请你依次写出最先检测的4颗种子的编号________.(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
2
题型讲解
[解析] 第8行第2列的数3开始向右读第一个小于850的数字是301,
第二个数字是637,也符合题意,
第三个数字是859,大于850,舍去,
第四个数字是169,符合题意,
第五个数字是555,符合题意,
故答案为:301,637,169,555.
2
题型讲解
【对点练习】(1) 一个单位有职工800人,其中具有高级职称的160人,具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层随机抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
A.12,24,15,9 B.9,12,12,7
C.8,15,12,5 D.8,16,10,6
D
2
题型讲解
C
2
题型讲解
025,016,105,185,395
2
题型讲解
与频率分布直方图有关问题的常见类型及解题策略
(1)已知频率分布直方图中的部分数据,求其他数据,可利用频率和等于1求解.
(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.
题型二 用样本的取值规律估计总体的取值规律
2
题型讲解
例1、下表给出了某校500名12岁男孩中用随机抽样得出的120人的身高资料(单位:cm):
(1)列出样本的频率分布表(频率保留两位小数);
(2)画出频率分布直方图;
(3)估计身高低于134 cm的人数占总人数的百分比.
区间界限 [122,126) [126,130) [130,134) [134,138) [138,142)
人数 5 8 10 22 33
区间界限 [142,146) [146,150) [150,154) [154,158]
人数 20 11 6 5
2
题型讲解
[解析] (1)列出样本频率分布表:
分组 频数 频率
[122,126) 5 0.04
[126,130) 8 0.07
[130,134) 10 0.08
[134,138) 22 0.18
[138,142) 33 0.28
[142,146) 20 0.17
[146,150) 11 0.09
[150,154) 6 0.05
[154,158] 5 0.04
合计 120 1.00
2
题型讲解
2
题型讲解
【对点练习】某电子商务公司对10 000名网络购物者2018年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
(1)直方图中的a=____;
(2)在这些购物者中,
消费金额在区间[0.5,0.9]内的
购物者的人数为________.
3
6 000
2
题型讲解
题型三 总体百分位数的估计
例1.某产品售后服务中心随机选取了10个工作日,分别记录了每个工作日接到的客户服务电话的数量(单位:次):
63 38 25 42 56 48 53 39 28 47
则上述数据的第50百分位数为________.
解析 把这组数据从小到大排序:25,28,38,39,42,47,48,53,56,63,
根据i=n×p%,计算得:i=10×50%=5.
因为i为整数,所以第p百分位数为第i项与第(i+1)项数据的平均数,即
2
题型讲解
例2.欧洲联盟委员会和荷兰环境评估署公布了2013年全球主要20个国家和地区的人均二氧化碳排放量,结果如下表:
国家和地区 人均排放 量/吨 国家和地区 人均排放 量/吨 国家和地区 人均排放
量/吨
中国 7.4 沙特阿拉伯 16.6 印度 1.7
美国 16.6 巴西 2.0 俄罗斯 12.6
欧盟 7.3 英国 7.5 日本 10.7
加拿大 15.7 墨西哥 3.9 德国 10.2
印度尼西亚 2.6 伊朗 5.3 韩国 12.7
意大利 6.4 澳大利亚 16.9 南非 6.2
法国 5.7 波兰 8.5
请计算这20个国家和地区的人均二氧化碳排放量的四分位数.
2
题型讲解
解:把这20个国家和地区的人均二氧化碳排放量按从小到大的顺序排列:1.7,2.0,2.6,3.9,5.3,5.7,6.2,6.4,7.3,7.4,7.5,8.5,10.2,10.7,12.6,12.7,15.7,16.6,16.6,16.9.
根据i=n×p%,计算得:i=20×25%=5.
因为i为整数,所以第p百分位数为第i项与第(i+1)项数据的平均数,即
第25百分位数为
同理可得,20×50%=10,所以这20个数的第50百分位数为
20×75%=15,所以这20个数的第75百分位数为
所以这20个国家和地区的人均二氧化碳排放量的四分位数为5.5,7.45,12.65.
2
题型讲解
例1.若样本x1,x2,x3,…,xn的平均数为7,方差为6,则对于3x1+1,3x2+1,3x3+1,…,3xn+1,下列结论正确的是( ).
(A)平均数是21,方差是6 (B)平均数是7,方差是54
(C)平均数是22,方差是6 (D)平均数是22,方差是54
如果数据x1 ,x2 ,… ,xn的平均数为 ,方差为s2,
则新数据ax1+b,ax2+b,… ,axn+b的平均数为 ,方差为 .
计算可得:
答案 D
题型四:数据的集中趋势和离散程度的估计
2
题型讲解
例2.某公司销售部有销售人员15人,为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
(1)求这15位销售人员该月销售量的平均数、中位数及众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额.
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
2
题型讲解
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
解 (1)根据平均数公式 ,计算可得:
因为数据出现次数最多的为210,所以众数也为210.
(3)我认为不合理.因为15人中有13人的销售额达不到320件.虽然320是这一组数据的平均数,但它却不能反映销售人员的一般水平.
根据题意,数据已由大到小排序,因为共15个数据,所以中位数为最中间的第7个数据,即210.
销售额应定为210件.这是由于210既是中位数,又是众数,是绝大部分人都能达到的销售额.
(2)
2
题型讲解
例3.甲、乙两位学生参加声乐大赛,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
现要从中选派一人参加声乐大赛,请你计算出平均成绩和方差,并分析选派哪位学生参加合适?
2
题型讲解
解 根据平均数公式 ,可得甲、乙两人成绩的平均数:
根据方差的计算公式, 可得甲、乙两名
学生成绩的方差分别为:
2
题型讲解
方差刻画了数据的离散程度或波动幅度.
方差越大,数据的离散程度越大,越不稳定.
方差越小,数据的离散程度越小,越稳定.
平均数反映了数据的集中趋势.
平均数 方差
甲 85 35.5
乙 85 41
所以甲的成绩较稳定,应派甲参赛.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
