人教版数学九年级下册 26.1.2反比例函数的图像和性质(第2课时)课件 (共43张PPT)
文档属性
| 名称 | 人教版数学九年级下册 26.1.2反比例函数的图像和性质(第2课时)课件 (共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 19:16:16 | ||
图片预览










文档简介
(共43张PPT)
第二十六章 反比例函数
6.1.2 反比例函数的图象和性质第2课时
学习目标
2.会用待定系数法求反比例函数解析式.
1.使学生进一步理解和掌握反比例函数的图象及性质 .
3.能灵活运用函数图象和性质解决一些较综合的问题.
学习目标:
温故知新
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号
________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
温故知新
(2)当 k<0 时,由于__________得负,因此可以判断 x,y
的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
温故知新
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
温故知新
二四象限
一三象限
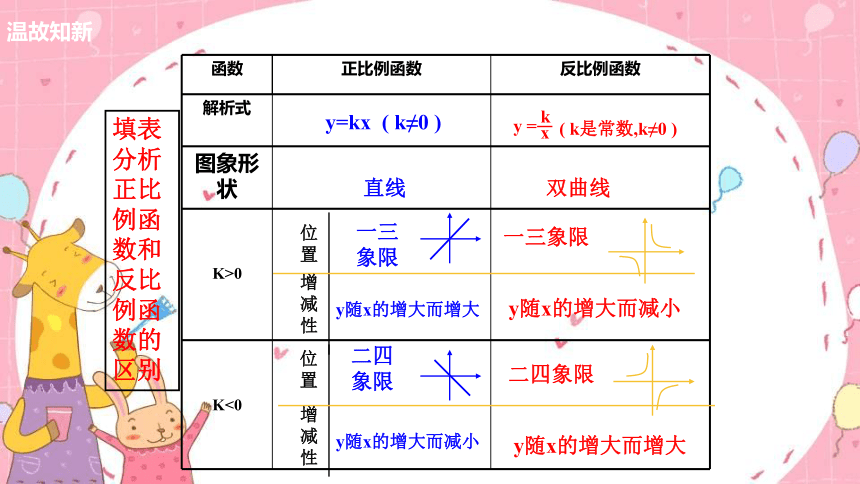
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
温故知新
知识巩固
1.函数 的图象在第_____象限,在每个象限内,y 随 x 的增大而_____ .
y =
x
5
4.对于函数 ,当 x<0时,y 随x的_____而
增大,这部分图象在第 ________象限.
y =
1
2x
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
m-2
x
y =
5.函数 , y 随 x 的减小而增大,
则m= ____.
y =(2m+1)xm+2m-16
2
二,四
减小
m < 2
三
3
增大
y =
1
3x
2. 双曲线 经过点(-3,___)
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限 y随x的增大如何变化
(2)点B(3,4)、C( )和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为 ,
解得: k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
知识巩固
跟踪训练
m﹥0
m -5= -1
所以必须满足{
1.已知反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
【解】因为反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,
y=mxm -5
x
y
0
2、下列各点在双曲线 上的是( )
A、( , ) B、( , )
C、( , ) D、( , )
B
跟踪训练
例2. 如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那 么b和b′有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得 m>5
跟踪训练
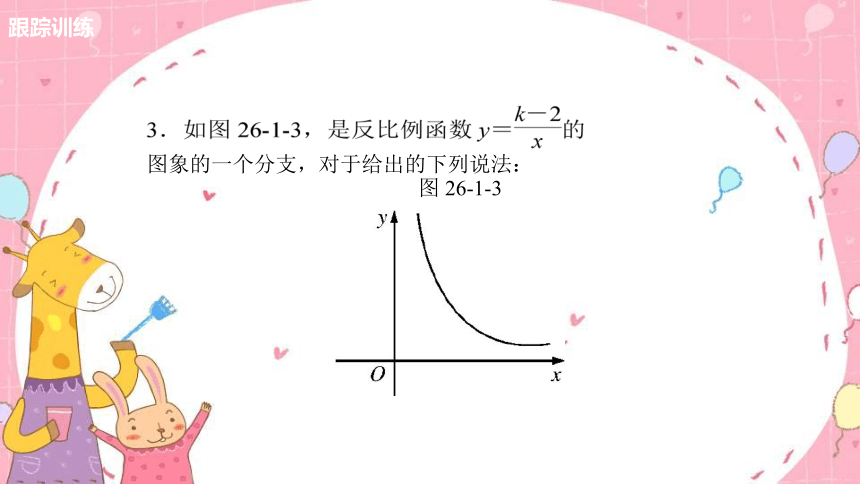
图象的一个分支,对于给出的下列说法:
图 26-1-3
跟踪训练
①常数 k 的取值范围是 k>2;
②另一个分支在第三象限;
③在函数图象上取点 A(a1 ,b1)和点 B(a2 ,b2),当 a1 >a2
时,则 b1<b2;
④在函数图象的某一个分支上取点 A(a1,b1)和点 B(a2,b2),
当 a1>a2 时,则 b1<b2.
其中正确的是 __________(在横线上填出正确的序号).
①②④
跟踪训练
练习
1、在反比例函数 的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),若x1>x2>0>x3,则下列各式中正确的是( )
A、y3>y1>y2 B、y3>y2>y1
C、y1>y2>y3 D、y1>y3>y2
A
知识点3 k的几何意义(知识拓展)
【例 3】 过如图 26-1-4 所示双曲线上任一点 P 作 x 轴、y
轴的垂线 PM、PN,求四边形 PMON 的面积.
图 26-1-4
技巧总结
若 P 在第四象限,或双曲线在第一、三象限,
则同样有 S 四边形PMON=|k|.
因此 k 的几何意义为:过双曲线上任意一点作 x 轴、y 轴的
垂线,所得的四边形的面积为|k|.
技巧总结
P
D
o
y
x
2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
S△POD = OD·PD
=
=
思考
反比例函数 上一点P(x0,y0),过点P作PA⊥y轴,PB⊥X轴,垂足分别为A、B,则四边形AOBP的面积为 ;且S△AOP S△BOP 。
=
技巧总结
面积性质(一)
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质(二)
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
根据象限确定k的符号
面积性质(二)
2.根据图中点的坐标
(1)求出y与x的函数解析式.
(2)如果点A(-2,b)在双曲线上,求b的值.
A(-2,b)
(3,-1)
x
0
(3)比较绿色部分和黄色部分的面积的大小.
.
B
y
(3)绿色部分和黄色部分的面积相等,都等于︱k︱
答案:(1) (2)
面积性质(二)
3.如图:A,B是双曲线y= 上的
任意两点.过A,B两点分别作x轴
和y轴的垂线,试确定图中两个三
角形的面积各是多少?
5
x
x
y
o
A
y=
5
x
B
答:面积都是 .
5
2
三角形的面积= ︱k︱
面积性质(二)
3.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
跟踪训练
图 26-1-5
为此图象上的一动点,过点 A 分别作 AB⊥x 轴和 AC⊥y 轴,垂
足分别为 B,C,则四边形 OBAC 周长的最小值为(
)
A.4
B.3
C.2
D.1
解析:要使四边形的周长最小,则需要四边形为正方形,
此时 OB=AB=AC=OC=1,所以周长为 4.
A
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
跟踪训练
6.如图: A、C是函数 的图象上任意两点,
A.S1>S2
B.S1C.S1 = S2
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
跟踪训练
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
跟踪训练
3、如图,已知反比例函数 的图象与一次函数
y= kx+4的图象相交于P、Q两点,且P点的纵坐标
是6。
(1)求这个一次函数的解析式
(2)求三角形POQ的面积
x
y
o
P
Q
D
C
跟踪训练
A
y
O
B
x
求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。
跟踪训练
例题
例4.(成都·中考)如图,已
知反比例函数 与一次函数y=x+b的
图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的解析式.
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
【解析】(1)把A点坐标代入反比例函数解析式得:-k+4=k,
解得k=2,把A(1,2)代入y=x+b
得b=1,∴这两个函数的解析式为:
y= 和y=x+1.
(2)由方程组
∴B点的坐标为(-2,-1).
由图象得反比例函数的值大于一次函数的值的x的取值范围是:0<x<1或x<-2.
例题
跟踪训练
跟踪训练
跟踪训练
随堂练习
随堂练习
3.(江津·中考)已知如图,A是反比例函
数 的图象上的一点,AB⊥x轴于点B,
且△ABO的面积是3,则k的值是( )
(A)3 (B)-3 (C)6 (D)-6
【解析】选C.设A点的坐标为(a,b),则k=ab,△ABO的
面积为 ,所以ab=6,即k=6
随堂练习
随堂练习
5.(威海·中考)如图,一次函数y=kx+b的图象与反比
例函数 的图象交于点A(-2,-5),C(5,n),
交y轴于点B,交x轴于点D.
(1)求反比例函数 和一次函数
y=kx+b的解析式;
(2)连接OA,OC.求△AOC的面积.
随堂练习
【解析】(1)∵反比例函数 的图象经过点A(-2,
-5),∴m=(-2)×(-5)=10.
∴反比例函数的解析式为
∵点C(5,n)在反比例函数的图象上,
∴n= =2.
∴C的坐标为(5,2).
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得 -5=-2k+b 解得 k=1
2=5k+b b=-3
∴所求一次函数的解析式为y=x-3.
{
{
随堂练习
(2)∵一次函数y=x-3的图象交y轴于点B,
∴B点坐标为(0,-3)
∴OB=3.
∵A点的横坐标为-2,C点的横坐标为5,
∴S△AOC=S△AOB+S△BOC= · OB · |-2|+ · OB · 5
= · OB ·(2+5)=
随堂练习
本课小结
通过本课时的学习,需要我们
1.熟练掌握反比例函数的图象及性质.
2.能用待定系数法求反比例函数解析式.
3.灵活运用函数图象和性质解决一些较综合的问题.
谢 谢!
第二十六章 反比例函数
6.1.2 反比例函数的图象和性质第2课时
学习目标
2.会用待定系数法求反比例函数解析式.
1.使学生进一步理解和掌握反比例函数的图象及性质 .
3.能灵活运用函数图象和性质解决一些较综合的问题.
学习目标:
温故知新
探究:y= (k≠0)可变形为 k=__________.
1.反比例函数的图象
xy
(1)当 k>0 时,由于______得正,因此可以判断 x,y 的符号
________,所以点(x,y)在____________象限,所以函数图象位
于__________象限.
相同
第一或第三
一、三
xy
温故知新
(2)当 k<0 时,由于__________得负,因此可以判断 x,y
的符号________,所以点(x,y)在____________象限,所以函数
图象位于__________象限.
二、四
归纳:反比例函数的图象是_______,它有_____分支.
两个
当 k>0 时,函数图象位于____________象限;
当 k<0 时,函数图象位于____________象限.
xy
相反
第二或第四
双曲线
一、三
二、四
温故知新
2.反比例函数的性质
(1)形状:________线.
双曲
(2)位置:k>0 时,图象在第________象限;
一、三
k<0 时,图象在第________象限.
二、四
(3)增减性:
k>0 时,在每一个象限内,y 随 x 的增大而______;
k<0 时,在每一个象限内,y 随 x 的增大而______.
减小
增大
温故知新
二四象限
一三象限
函数 正比例函数 反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
y随x的增大而增大
一三象限
y随x的增大而减小
二四象限
y随x的增大而减小
y随x的增大而增大
填表分析正比例函数和反比例函数的区别
温故知新
知识巩固
1.函数 的图象在第_____象限,在每个象限内,y 随 x 的增大而_____ .
y =
x
5
4.对于函数 ,当 x<0时,y 随x的_____而
增大,这部分图象在第 ________象限.
y =
1
2x
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
m-2
x
y =
5.函数 , y 随 x 的减小而增大,
则m= ____.
y =(2m+1)xm+2m-16
2
二,四
减小
m < 2
三
3
增大
y =
1
3x
2. 双曲线 经过点(-3,___)
例1.已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限 y随x的增大如何变化
(2)点B(3,4)、C( )和D(2,5)是否在这个函数的图象上?
解:(1)设这个反比例函数为 ,
解得: k=12
∴这个反比例函数的表达式为
∵k>0
∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。
∵图象过点A(2,6)
知识巩固
跟踪训练
m﹥0
m -5= -1
所以必须满足{
1.已知反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
【解】因为反比例函数y=mxm -5,它的两个分支分别在第一、第三象限,
y=mxm -5
x
y
0
2、下列各点在双曲线 上的是( )
A、( , ) B、( , )
C、( , ) D、( , )
B
跟踪训练
例2. 如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那 么b和b′有怎样的大小关系?
解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得 m>5
跟踪训练
图象的一个分支,对于给出的下列说法:
图 26-1-3
跟踪训练
①常数 k 的取值范围是 k>2;
②另一个分支在第三象限;
③在函数图象上取点 A(a1 ,b1)和点 B(a2 ,b2),当 a1 >a2
时,则 b1<b2;
④在函数图象的某一个分支上取点 A(a1,b1)和点 B(a2,b2),
当 a1>a2 时,则 b1<b2.
其中正确的是 __________(在横线上填出正确的序号).
①②④
跟踪训练
练习
1、在反比例函数 的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),若x1>x2>0>x3,则下列各式中正确的是( )
A、y3>y1>y2 B、y3>y2>y1
C、y1>y2>y3 D、y1>y3>y2
A
知识点3 k的几何意义(知识拓展)
【例 3】 过如图 26-1-4 所示双曲线上任一点 P 作 x 轴、y
轴的垂线 PM、PN,求四边形 PMON 的面积.
图 26-1-4
技巧总结
若 P 在第四象限,或双曲线在第一、三象限,
则同样有 S 四边形PMON=|k|.
因此 k 的几何意义为:过双曲线上任意一点作 x 轴、y 轴的
垂线,所得的四边形的面积为|k|.
技巧总结
P
D
o
y
x
2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
(m,n)
1
S△POD = OD·PD
=
=
思考
反比例函数 上一点P(x0,y0),过点P作PA⊥y轴,PB⊥X轴,垂足分别为A、B,则四边形AOBP的面积为 ;且S△AOP S△BOP 。
=
技巧总结
面积性质(一)
P(m,n)
A
o
y
x
P(m,n)
A
o
y
x
面积性质(二)
P(m,n)
A
o
y
x
B
P(m,n)
A
o
y
x
B
根据象限确定k的符号
面积性质(二)
2.根据图中点的坐标
(1)求出y与x的函数解析式.
(2)如果点A(-2,b)在双曲线上,求b的值.
A(-2,b)
(3,-1)
x
0
(3)比较绿色部分和黄色部分的面积的大小.
.
B
y
(3)绿色部分和黄色部分的面积相等,都等于︱k︱
答案:(1) (2)
面积性质(二)
3.如图:A,B是双曲线y= 上的
任意两点.过A,B两点分别作x轴
和y轴的垂线,试确定图中两个三
角形的面积各是多少?
5
x
x
y
o
A
y=
5
x
B
答:面积都是 .
5
2
三角形的面积= ︱k︱
面积性质(二)
3.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
跟踪训练
图 26-1-5
为此图象上的一动点,过点 A 分别作 AB⊥x 轴和 AC⊥y 轴,垂
足分别为 B,C,则四边形 OBAC 周长的最小值为(
)
A.4
B.3
C.2
D.1
解析:要使四边形的周长最小,则需要四边形为正方形,
此时 OB=AB=AC=OC=1,所以周长为 4.
A
的图象交于点 M(a,1),MN⊥x 轴于点N(如图 26-1-6),若△OMN
的面积等于 2,求这两个函数的解析式.
图 26-1-6
跟踪训练
6.如图: A、C是函数 的图象上任意两点,
A.S1>S2
B.S1
D.S1和S2的大小关系不能确定.
C
A
B
o
y
x
C
D
D
S1
S2
跟踪训练
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
跟踪训练
3、如图,已知反比例函数 的图象与一次函数
y= kx+4的图象相交于P、Q两点,且P点的纵坐标
是6。
(1)求这个一次函数的解析式
(2)求三角形POQ的面积
x
y
o
P
Q
D
C
跟踪训练
A
y
O
B
x
求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。
跟踪训练
例题
例4.(成都·中考)如图,已
知反比例函数 与一次函数y=x+b的
图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的解析式.
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出反比例函数的值大于一次函数的值的x的取值范围.
【解析】(1)把A点坐标代入反比例函数解析式得:-k+4=k,
解得k=2,把A(1,2)代入y=x+b
得b=1,∴这两个函数的解析式为:
y= 和y=x+1.
(2)由方程组
∴B点的坐标为(-2,-1).
由图象得反比例函数的值大于一次函数的值的x的取值范围是:0<x<1或x<-2.
例题
跟踪训练
跟踪训练
跟踪训练
随堂练习
随堂练习
3.(江津·中考)已知如图,A是反比例函
数 的图象上的一点,AB⊥x轴于点B,
且△ABO的面积是3,则k的值是( )
(A)3 (B)-3 (C)6 (D)-6
【解析】选C.设A点的坐标为(a,b),则k=ab,△ABO的
面积为 ,所以ab=6,即k=6
随堂练习
随堂练习
5.(威海·中考)如图,一次函数y=kx+b的图象与反比
例函数 的图象交于点A(-2,-5),C(5,n),
交y轴于点B,交x轴于点D.
(1)求反比例函数 和一次函数
y=kx+b的解析式;
(2)连接OA,OC.求△AOC的面积.
随堂练习
【解析】(1)∵反比例函数 的图象经过点A(-2,
-5),∴m=(-2)×(-5)=10.
∴反比例函数的解析式为
∵点C(5,n)在反比例函数的图象上,
∴n= =2.
∴C的坐标为(5,2).
∵一次函数的图象经过点A,C,将这两个点的坐标代入y=kx+b,得 -5=-2k+b 解得 k=1
2=5k+b b=-3
∴所求一次函数的解析式为y=x-3.
{
{
随堂练习
(2)∵一次函数y=x-3的图象交y轴于点B,
∴B点坐标为(0,-3)
∴OB=3.
∵A点的横坐标为-2,C点的横坐标为5,
∴S△AOC=S△AOB+S△BOC= · OB · |-2|+ · OB · 5
= · OB ·(2+5)=
随堂练习
本课小结
通过本课时的学习,需要我们
1.熟练掌握反比例函数的图象及性质.
2.能用待定系数法求反比例函数解析式.
3.灵活运用函数图象和性质解决一些较综合的问题.
谢 谢!
