6.1.1向量的概念 课件(共15张PPT)
文档属性
| 名称 | 6.1.1向量的概念 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 819.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 10:49:26 | ||
图片预览






文档简介
(共15张PPT)
向量的概念
问题提出
1.在物理中,位移与距离是同一个概念吗?为什么?
2.现实世界中有各种各样的量,如年龄、身高、体重、力、速度、面积、体积、温度等,在数学上,为了正确理解、区分这些量,我们引进向量的概念.
向量的物理背景、概念和几何表示
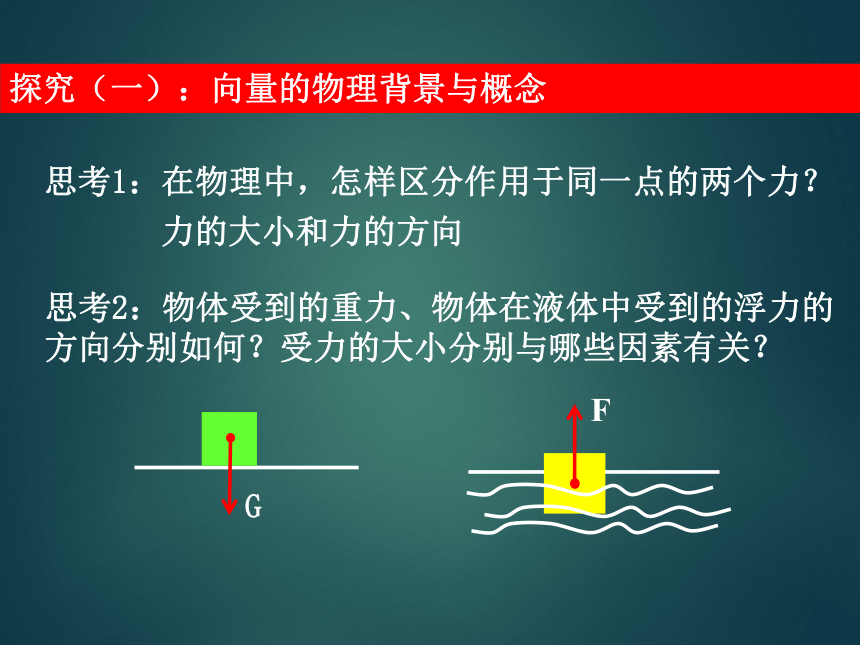
探究(一):向量的物理背景与概念
思考1:在物理中,怎样区分作用于同一点的两个力?
力的大小和力的方向
思考2:物体受到的重力、物体在液体中受到的浮力的方向分别如何?受力的大小分别与哪些因素有关?
G
F
思考3:在如图所示的弹簧中,被拉长或压缩的弹簧的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
思考4:力既有大小,又有方向,在物理学中称为矢量,你还能指出哪些物理量是矢量吗?
思考5:数学中,把既有大小,又有方向的量叫做向量,把只有大小,没有方向的量称为数量.那么年龄、身高、体重、面积、体积、温度、时间、路程、数轴等是向量吗?
探究(二):向量的几何表示
思考1:一条小船从A地出发,向西北方向航行15km到达B地,可以用什么方式表示小船的位移?
B
A
东
北
思考2:对于一个实数,可以用数轴上的点表示;对于一个角的正弦、余弦和正切,可以用三角函数线表示;对于一个二次函数,可以用一条抛物线表示….数学中有许多量都可以用几何方式表示,你认为如何用几何方式表示向量最合适?
思考3:如图,以A为起点、B为终点的有向线段记作AB ,一条有向线段由哪几个基本要素所确定?
A(起点)
B(终点)
思考4:用有向线段 AB 表示向量,向量AB 的大小和方向是如何反映出来的?
起点、长度、方向
思考5:有向线段 的长度就是指线段AB的长度,也称为向量 的长度或模,它表示向量 的大小,记作| |,两个不同的向量可以比较大小吗?
思考6:如果表示向量的有向线段没有标注起点和终点字母,向量也可以用黑体字母a,b,c,…,或 表示,如图.
此时向量的模怎样表示?
a
思考7:向量的模可以为0吗?可以为1吗?可以为负数吗?
思考8:模为0的向量叫做零向量,记作 ;模为1个单位的向量叫做单位向量.怎样理解零向量的方向?怎样理解向量 ?
理论迁移
例1 已知飞机从A地按北偏东30°方向飞行2000km到达B地,再从B地按南偏东30°方向飞行2000km到达C地,再从C地按西南方向飞行1000 km到达D地.
(1)画图表示向量 ;
(2)求飞机从A地到达D地的位移所对应的向量的模和方向.
B
A
东
北
C
D
例2 如图,四边形ABCD为正方形,△BCE为等腰直角三角形.以图中各点为起点和终点,写出与向量 模相等的所有向量.
A
B
C
D
E
小结作业
1.向量是为了表示、刻画既有大小,又有方向的量而产生的,物理中有许多相关背景材料,数学中的向量是物理中矢量的提升和拓展,它有一系列的理论和方法,是沟通代数、几何、三角的一种工具,有着广泛的实际应用.
2.由于有向线段具有长度和方向双重特征,所以向量可以用有向线段表示,但向量不是有向线段,二者只是一种对应关系.
3.零向量是一个特殊向量,其模为0,方向是不确定的.引入零向量将为以后的研究带来许多方便.
向量的概念
问题提出
1.在物理中,位移与距离是同一个概念吗?为什么?
2.现实世界中有各种各样的量,如年龄、身高、体重、力、速度、面积、体积、温度等,在数学上,为了正确理解、区分这些量,我们引进向量的概念.
向量的物理背景、概念和几何表示
探究(一):向量的物理背景与概念
思考1:在物理中,怎样区分作用于同一点的两个力?
力的大小和力的方向
思考2:物体受到的重力、物体在液体中受到的浮力的方向分别如何?受力的大小分别与哪些因素有关?
G
F
思考3:在如图所示的弹簧中,被拉长或压缩的弹簧的弹力方向如何?在弹性限度内,弹力的大小与什么因素有关?
思考4:力既有大小,又有方向,在物理学中称为矢量,你还能指出哪些物理量是矢量吗?
思考5:数学中,把既有大小,又有方向的量叫做向量,把只有大小,没有方向的量称为数量.那么年龄、身高、体重、面积、体积、温度、时间、路程、数轴等是向量吗?
探究(二):向量的几何表示
思考1:一条小船从A地出发,向西北方向航行15km到达B地,可以用什么方式表示小船的位移?
B
A
东
北
思考2:对于一个实数,可以用数轴上的点表示;对于一个角的正弦、余弦和正切,可以用三角函数线表示;对于一个二次函数,可以用一条抛物线表示….数学中有许多量都可以用几何方式表示,你认为如何用几何方式表示向量最合适?
思考3:如图,以A为起点、B为终点的有向线段记作AB ,一条有向线段由哪几个基本要素所确定?
A(起点)
B(终点)
思考4:用有向线段 AB 表示向量,向量AB 的大小和方向是如何反映出来的?
起点、长度、方向
思考5:有向线段 的长度就是指线段AB的长度,也称为向量 的长度或模,它表示向量 的大小,记作| |,两个不同的向量可以比较大小吗?
思考6:如果表示向量的有向线段没有标注起点和终点字母,向量也可以用黑体字母a,b,c,…,或 表示,如图.
此时向量的模怎样表示?
a
思考7:向量的模可以为0吗?可以为1吗?可以为负数吗?
思考8:模为0的向量叫做零向量,记作 ;模为1个单位的向量叫做单位向量.怎样理解零向量的方向?怎样理解向量 ?
理论迁移
例1 已知飞机从A地按北偏东30°方向飞行2000km到达B地,再从B地按南偏东30°方向飞行2000km到达C地,再从C地按西南方向飞行1000 km到达D地.
(1)画图表示向量 ;
(2)求飞机从A地到达D地的位移所对应的向量的模和方向.
B
A
东
北
C
D
例2 如图,四边形ABCD为正方形,△BCE为等腰直角三角形.以图中各点为起点和终点,写出与向量 模相等的所有向量.
A
B
C
D
E
小结作业
1.向量是为了表示、刻画既有大小,又有方向的量而产生的,物理中有许多相关背景材料,数学中的向量是物理中矢量的提升和拓展,它有一系列的理论和方法,是沟通代数、几何、三角的一种工具,有着广泛的实际应用.
2.由于有向线段具有长度和方向双重特征,所以向量可以用有向线段表示,但向量不是有向线段,二者只是一种对应关系.
3.零向量是一个特殊向量,其模为0,方向是不确定的.引入零向量将为以后的研究带来许多方便.
