7.2万有引力定律课件-2021-2022学年高一下学期物理人教版(2019)必修第二册(共22张ppt)
文档属性
| 名称 | 7.2万有引力定律课件-2021-2022学年高一下学期物理人教版(2019)必修第二册(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 11.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-12 10:45:27 | ||
图片预览





文档简介
(共22张PPT)
教材人教版 物理(高中必修第二册)
7.2 万有引力定律
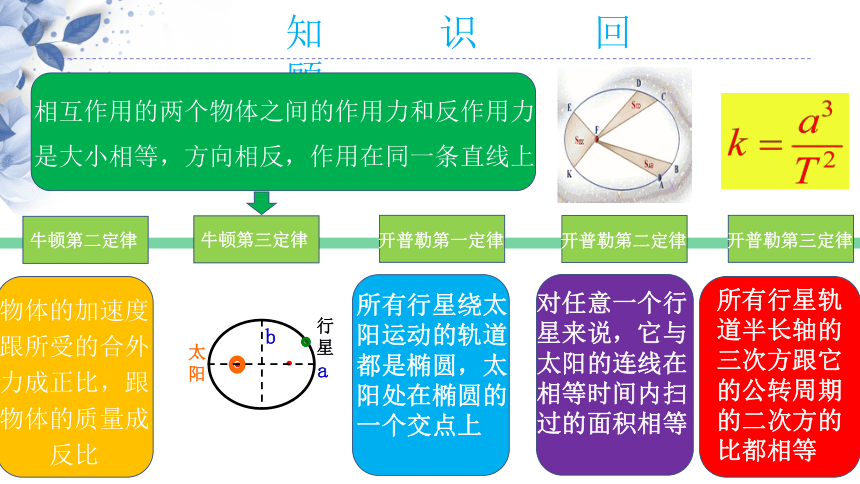
知 识 回 顾
物体的加速度跟所受的合外力成正比,跟物体的质量成反比
所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个交点上
太阳
行星
b
a
对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等
牛顿第二定律
牛顿第三定律
开普勒第一定律
开普勒第二定律
开普勒第三定律
所有行星轨道半长轴的三次方跟它的公转周期的二次方的比都相等
相互作用的两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上。
新 课 引 入
1666年夏末一个温暖的夜晚,在英格兰林肯郡乌尔斯索普,一个腋下夹着一本书的年轻人走进他母亲的花园,坐在一棵树下,开始埋头读书。
当他翻动书页时,他头顶的树枝中有样东西晃动起来,一个历史上最著名的苹果落了下来,正好打在23岁的牛顿头上。恰巧在这天,牛顿正苦苦思考着一个问题:是什么力量使月球保持在环绕地球运行的轨道上?又是什么力量使行星保持在环绕太阳运行的轨道上?为什么这个打中他脑袋的苹果会坠落到地上?于是…….
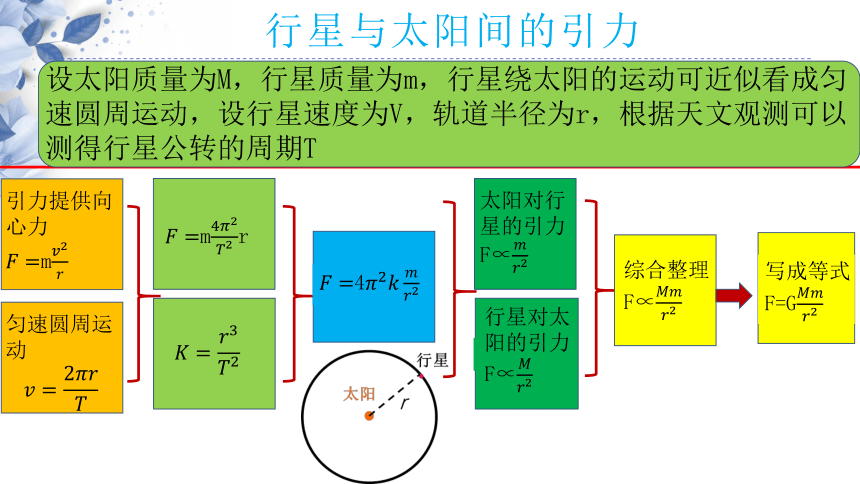
行星与太阳间的引力
设太阳质量为M,行星质量为m,行星绕太阳的运动可近似看成匀速圆周运动,设行星速度为V,轨道半径为r,根据天文观测可以测得行星公转的周期T
引力提供向心力
m
匀速圆周运动
mr
4
F∝
F=G
太阳对行星的引力
F∝
行星对太阳的引力
F∝
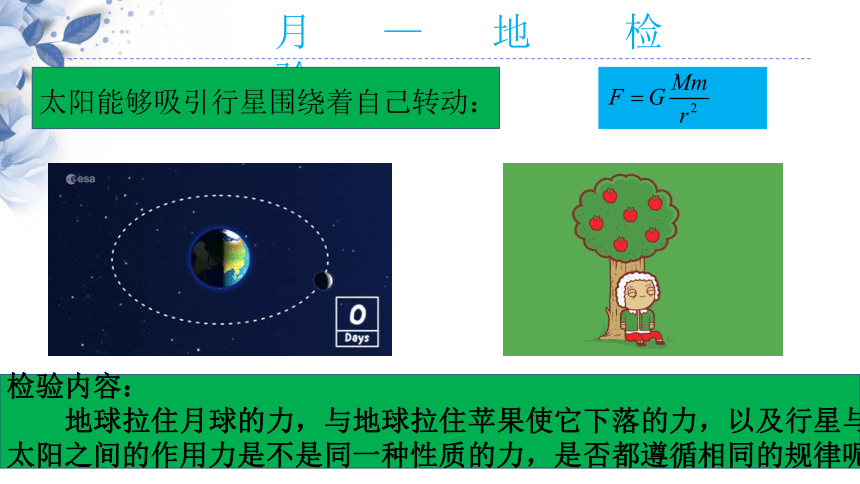
月 — 地 检 验
太阳能够吸引行星围绕着自己转动:
检验内容:
地球拉住月球的力,与地球拉住苹果使它下落的力,以及行星与太阳之间的作用力是不是同一种性质的力,是否都遵循相同的规律呢
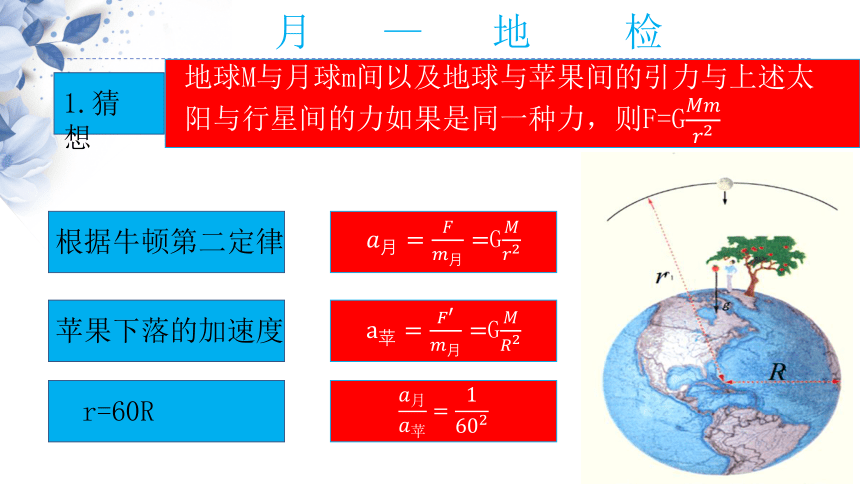
月 — 地 检 验
1.猜想
地球M与月球m间以及地球与苹果间的引力与上述太阳与行星间的力如果是同一种力,则F=G
根据牛顿第二定律
G
苹果下落的加速度
G
r=60R
月 — 地 检 验
1.验证
(1)苹果自由落体加速度a苹=g=9.8 m/
2.7
即
(2)月球中心距地球中心的距离r=3.8m.
(3)月球公转周期T=27.3天2.36
3.结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,遵从相同的规律.
万 有 引 力 定 律
1.内容
自然界中任何两个 物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量和的乘积成正比、与它们之间距离r的二次方成反比
2.表达式
F=G
3.适用条件
质点间引力计算
4.引力常量
G=6.67N·(卡文迪什扭秤实验)
对两个质量分布均匀的球体间相互作用,也可用此定律来计算。此时,r是两个球体球心间的距离。
随 堂 练 习
1.判断下列说法的正误
(1)万有引力不仅存在于天体之间,也存在于普通物体之间 ( )
(3)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大. ( )
(5) 太阳质量大,故太阳对行星的引力大于行星对太阳引力. ( )
√
(2)牛顿发现了万有引力定律,并测出了引力常量. ( )
×
×
×
随 堂 练 习
2.(多选)关于太阳与行星间的引力,下列说法中正确的是( )
A.由于地球比木星离太阳近,所以太阳对地球的引力一定比对木星的引力大
B.行星绕太阳沿椭圆轨道运动时,在从近日点向远日点运动时所受引力变小
C.由F= 可知G= ,由此可见G与F和r2的乘积成正比,与M太和m的乘积成反比
D.行星绕太阳运动的椭圆轨道可近似看成圆轨道,行星做圆周运动的向心力来源于太阳对行星的引力
BD
随 堂 练 习
2. .2021年4 月 29 日 11 时 22 分我国空间站“天和”核心舱发射成功。在地球引力作用下,绕地球做匀速圆周运动,已知地球的质量为M,地球的半径为R,“天和”的质量为m,离地面的高度为h,引力常量为G,则地球对“天和”的万有引力大小为( )
A. B.
C. D.
A
随 堂 练 习
3.如图2所示,两球间的距离为.两球的质量分布均匀,质量分别为、,半径分别为、,则两球间的万有引力大小为 ( )
D
随 堂 练 习
2.通过本节所学,一切物体间都存在万有引力。为什么通常两个人(假设两人可看成质点,质量均为100 kg,相距1 m)之间的万有引力我们却感受不到?
解析两个人之间的万有引力大小为:
= ×100×100∕=6.67× N,因引力很小,所以通常感受不到.
随 堂 练 习
2.通过本节所学,一切物体间都存在万有引力。为什么通常两个人(假设两人可看成质点,质量均为100 kg,相距1 m)之间的万有引力我们却感受不到?
解析两个人之间的万有引力大小为:
= ×100×100∕=6.67× N,因引力很小,所以通常感受不到.
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
1. 人在不同位置受到的万有引力的大小和方向?
将地球视为一个规则的球体
将地球视为一个规则的球体
将人视为一个质点
方向均由人沿半径指向地心。
四、万有引力和重力的关系
O
w
引
引
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
2. 人在不同位置,什么力提供向心力?
引
向
mg
向
向心力由万有引力的一个分力去充当。
按照矢量的平行四边形法则,万有引力还会有另一个分力——就是我们以前学过的重力。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
3. 人在北极点的受力分析(南极点的情况相同)
引
= 0
向
= mg
引
= 0
向
mg =
引
此时重力加速度 g 最大,
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
4. 人在赤道上的受力分析
引
向
mg
引
向
+ mg
引
此时重力加速度 g 最小。
向
mg =
引
向
从赤道到两极:随着纬度增加,向心力减小,重力mg在增大,重力加速度g增大。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
5. 若是忽略地球的自转,则不考虑向心力,即物体受到的万有引力总是等于物体的重力。
引
mg
地球自转的角速度:
在同一纬度,距地面越高,重力加速度越小。
四、万有引力和重力的关系
重力与高度的关系
O
R
h
若距离地面的高度为h,则:
(2)质量分布均匀的空心球对内部的质点:
1. 空心球对质点的万有引力
五、空心球对质点的万有引力
(1)质量分布均匀的空心球对外部的质点:
r
m
R
M
R
M
m
R
M
m
质点在空心球内的中心
质点在空心球内的任意位置
万有引力的合力为零。
教材人教版 物理(高中必修第二册)
7.2 万有引力定律
知 识 回 顾
物体的加速度跟所受的合外力成正比,跟物体的质量成反比
所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个交点上
太阳
行星
b
a
对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等
牛顿第二定律
牛顿第三定律
开普勒第一定律
开普勒第二定律
开普勒第三定律
所有行星轨道半长轴的三次方跟它的公转周期的二次方的比都相等
相互作用的两个物体之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上。
新 课 引 入
1666年夏末一个温暖的夜晚,在英格兰林肯郡乌尔斯索普,一个腋下夹着一本书的年轻人走进他母亲的花园,坐在一棵树下,开始埋头读书。
当他翻动书页时,他头顶的树枝中有样东西晃动起来,一个历史上最著名的苹果落了下来,正好打在23岁的牛顿头上。恰巧在这天,牛顿正苦苦思考着一个问题:是什么力量使月球保持在环绕地球运行的轨道上?又是什么力量使行星保持在环绕太阳运行的轨道上?为什么这个打中他脑袋的苹果会坠落到地上?于是…….
行星与太阳间的引力
设太阳质量为M,行星质量为m,行星绕太阳的运动可近似看成匀速圆周运动,设行星速度为V,轨道半径为r,根据天文观测可以测得行星公转的周期T
引力提供向心力
m
匀速圆周运动
mr
4
F∝
F=G
太阳对行星的引力
F∝
行星对太阳的引力
F∝
月 — 地 检 验
太阳能够吸引行星围绕着自己转动:
检验内容:
地球拉住月球的力,与地球拉住苹果使它下落的力,以及行星与太阳之间的作用力是不是同一种性质的力,是否都遵循相同的规律呢
月 — 地 检 验
1.猜想
地球M与月球m间以及地球与苹果间的引力与上述太阳与行星间的力如果是同一种力,则F=G
根据牛顿第二定律
G
苹果下落的加速度
G
r=60R
月 — 地 检 验
1.验证
(1)苹果自由落体加速度a苹=g=9.8 m/
2.7
即
(2)月球中心距地球中心的距离r=3.8m.
(3)月球公转周期T=27.3天2.36
3.结论:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,遵从相同的规律.
万 有 引 力 定 律
1.内容
自然界中任何两个 物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量和的乘积成正比、与它们之间距离r的二次方成反比
2.表达式
F=G
3.适用条件
质点间引力计算
4.引力常量
G=6.67N·(卡文迪什扭秤实验)
对两个质量分布均匀的球体间相互作用,也可用此定律来计算。此时,r是两个球体球心间的距离。
随 堂 练 习
1.判断下列说法的正误
(1)万有引力不仅存在于天体之间,也存在于普通物体之间 ( )
(3)质量一定的两个物体,若距离无限小,它们间的万有引力趋于无限大. ( )
(5) 太阳质量大,故太阳对行星的引力大于行星对太阳引力. ( )
√
(2)牛顿发现了万有引力定律,并测出了引力常量. ( )
×
×
×
随 堂 练 习
2.(多选)关于太阳与行星间的引力,下列说法中正确的是( )
A.由于地球比木星离太阳近,所以太阳对地球的引力一定比对木星的引力大
B.行星绕太阳沿椭圆轨道运动时,在从近日点向远日点运动时所受引力变小
C.由F= 可知G= ,由此可见G与F和r2的乘积成正比,与M太和m的乘积成反比
D.行星绕太阳运动的椭圆轨道可近似看成圆轨道,行星做圆周运动的向心力来源于太阳对行星的引力
BD
随 堂 练 习
2. .2021年4 月 29 日 11 时 22 分我国空间站“天和”核心舱发射成功。在地球引力作用下,绕地球做匀速圆周运动,已知地球的质量为M,地球的半径为R,“天和”的质量为m,离地面的高度为h,引力常量为G,则地球对“天和”的万有引力大小为( )
A. B.
C. D.
A
随 堂 练 习
3.如图2所示,两球间的距离为.两球的质量分布均匀,质量分别为、,半径分别为、,则两球间的万有引力大小为 ( )
D
随 堂 练 习
2.通过本节所学,一切物体间都存在万有引力。为什么通常两个人(假设两人可看成质点,质量均为100 kg,相距1 m)之间的万有引力我们却感受不到?
解析两个人之间的万有引力大小为:
= ×100×100∕=6.67× N,因引力很小,所以通常感受不到.
随 堂 练 习
2.通过本节所学,一切物体间都存在万有引力。为什么通常两个人(假设两人可看成质点,质量均为100 kg,相距1 m)之间的万有引力我们却感受不到?
解析两个人之间的万有引力大小为:
= ×100×100∕=6.67× N,因引力很小,所以通常感受不到.
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
1. 人在不同位置受到的万有引力的大小和方向?
将地球视为一个规则的球体
将地球视为一个规则的球体
将人视为一个质点
方向均由人沿半径指向地心。
四、万有引力和重力的关系
O
w
引
引
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
2. 人在不同位置,什么力提供向心力?
引
向
mg
向
向心力由万有引力的一个分力去充当。
按照矢量的平行四边形法则,万有引力还会有另一个分力——就是我们以前学过的重力。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
3. 人在北极点的受力分析(南极点的情况相同)
引
= 0
向
= mg
引
= 0
向
mg =
引
此时重力加速度 g 最大,
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
4. 人在赤道上的受力分析
引
向
mg
引
向
+ mg
引
此时重力加速度 g 最小。
向
mg =
引
向
从赤道到两极:随着纬度增加,向心力减小,重力mg在增大,重力加速度g增大。
将地球视为一个规则的球体
四、万有引力和重力的关系
O
w
由于地球的自转,地面不同位置的人会做半径不同的匀速圆周运动:
5. 若是忽略地球的自转,则不考虑向心力,即物体受到的万有引力总是等于物体的重力。
引
mg
地球自转的角速度:
在同一纬度,距地面越高,重力加速度越小。
四、万有引力和重力的关系
重力与高度的关系
O
R
h
若距离地面的高度为h,则:
(2)质量分布均匀的空心球对内部的质点:
1. 空心球对质点的万有引力
五、空心球对质点的万有引力
(1)质量分布均匀的空心球对外部的质点:
r
m
R
M
R
M
m
R
M
m
质点在空心球内的中心
质点在空心球内的任意位置
万有引力的合力为零。
