北师大版九年级下册 2.5 二次函数与一元二次方程课件(共25张PPT)
文档属性
| 名称 | 北师大版九年级下册 2.5 二次函数与一元二次方程课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 14:55:28 | ||
图片预览








文档简介
(共25张PPT)
第二章 二次函数
2.5 二次函数与一元二次方程
1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不等的实数根、两个相等的实数根和没有实数根.
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.
学习目标
1.一元二次方程ax2+bx+c=0 的求根公式是什么?
当b2-4ac≥0时,
当b2-4ac<0时,方程无实数根.
新课导入
2.解下列一元二次方程:
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0.
解:(1)x1=0, x2=-2.
(2)x1=x2=1.
(3)没有实数根.
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t (s)的关系可以用公式
h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面
的高度,v0 (m/s)是抛出时
的速度.一个小球从地面被
以40 m/s的速度竖直向上抛
起,小球的高度h (m)与运
动时间t(s)的关系如图所示,
那么
O
h/m
t/s
1 2 3 4 5 6 7 8
80
70
60
50
40
30
20
10
知识讲解
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?你有几种求解方法?与同伴交流.
解析:(1)由图象知函数过点(0,0)与点(8,0)
代入关系式h=-5t2+v0t+h0得h0=0, 由已知可知v0=40,
得h=-5t2+40t.
(2)由图象可知小球经过8秒后落地.可以令h=0,得t=0s(舍去)或t=8s.
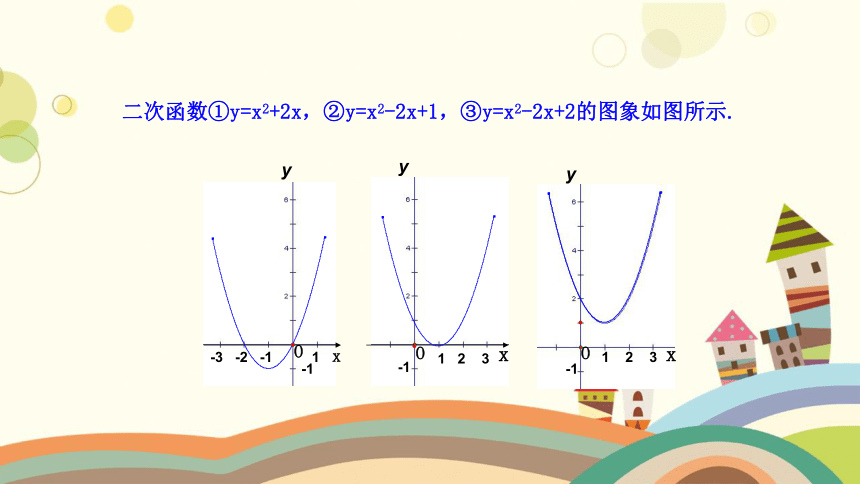
二次函数①y=x2+2x,②y=x2-2x+1,③y=x2-2x+2的图象如图所示.
-1
1
-3 -2 -1
O
x
y
-1
1 2 3
y
x
O
-1
1 2 3
O
y
x
(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个根?
解方程验证一下,一元二次方程x2-2x+2=0有根吗?
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
(2)①x1=0, x2=-2,两个不相等实数根.
②x1=x2=1,两个相等实数根.
③没有实数根.
解:(1)每个图象与x轴的交点个数分别是2个,1个,0个.
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
【规律方法】二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:
有两个交点、有一个交点、没有交点.
当二次函数y=ax2+bx+c的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
例:利用二次函数的图象求方程x2-x-3=0的实数根(精确到0.1).
x
y
用你学过的一元二次方程的解法来解,
准确答案是什么?
方法: (1)先作出y=x -x-3的图象;
(2)写出交点的坐标:
(-1.3,0),(2.3,0)
(3)得出方程的解:
x1=-1.3,x2=2.3.
【例题】
C
A
【跟踪训练】
3.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点
情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
C
4.根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A.3C.3.24x 3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
6.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方
程ax2+bx+c=0的解是 .
x
y
0
5
x1=0,x2=5
7.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实
数根,则m=__,此时抛物线 y=x2-2x+m与x轴有__个交
点.
8.已知抛物线 y=x2–8x+c的顶点在 x轴上,则c=__.
9.一元二次方程3x2+x-10=0的两个根是x1=-2,x2= ,
那么二次函数y=3x2+x-10与x轴的交点坐标是____和
___________.
1
1
16
( ,0)
(-2,0)
1.(崇左·中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;②方程ax2+bx+c=0的根为x1=
-1,x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,-1<x<3.其中正确的说法是( )
A.① B.①②
C.①②③ D.①②③④
O
x
y
1
3
-1
答案:D
随堂练习
2.(河北·中考)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)
O
x
y
A
x = 2
B
答案:D
3.(汕头·中考)已知二次函数y=-x2+bx+c的图象如图
所示,它与x轴的一个交点坐标为(-1,0),与y轴的
交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
【解析】(1)由题意得
解得
故所求解析式为
解得
∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.
(2)令
∴抛物线与x轴的另一个交点坐标为(3,0),
4.(株洲·中考)二次函数y=x2-mx+3的图象与x轴的交点如图所示,根据图中信息可得到m的值是_______.
答案:4
5.(咸宁·中考)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
由(1)得
∴二次函数的最小值为-4.
【解析】(1)依题意,m,-3m是一元二次方程
的两根.根据一元二次方程根与系数的
关系,得 ,
∴
,
,
(2)依题意,
,
,
,
1.二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
2.根据一元二次方程ax2+bx+c=0根的情况是两个不相等的实根、两个相等实根、没有实数根,图象上对应与x轴的交点个数是两个、一个、没有.
第二章 二次函数
2.5 二次函数与一元二次方程
1.经历探索二次函数与一元二次方程的关系的过程,体会方程与函数之间的联系.
2.理解二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系,理解何时方程有两个不等的实数根、两个相等的实数根和没有实数根.
3.理解一元二次方程的根就是二次函数与x轴交点的横坐标.
学习目标
1.一元二次方程ax2+bx+c=0 的求根公式是什么?
当b2-4ac≥0时,
当b2-4ac<0时,方程无实数根.
新课导入
2.解下列一元二次方程:
(1)x2+2x=0 (2)x2-2x+1=0 (3)x2-2x+2=0.
解:(1)x1=0, x2=-2.
(2)x1=x2=1.
(3)没有实数根.
我们已经知道,竖直上抛物体的高度 h (m) 与运动时间t (s)的关系可以用公式
h=-5t2+v0t +h0 表示,
其中h0 (m)是抛出点距地面
的高度,v0 (m/s)是抛出时
的速度.一个小球从地面被
以40 m/s的速度竖直向上抛
起,小球的高度h (m)与运
动时间t(s)的关系如图所示,
那么
O
h/m
t/s
1 2 3 4 5 6 7 8
80
70
60
50
40
30
20
10
知识讲解
(1)h与t 的关系式是什么?
(2)小球经过多少秒后落地?你有几种求解方法?与同伴交流.
解析:(1)由图象知函数过点(0,0)与点(8,0)
代入关系式h=-5t2+v0t+h0得h0=0, 由已知可知v0=40,
得h=-5t2+40t.
(2)由图象可知小球经过8秒后落地.可以令h=0,得t=0s(舍去)或t=8s.
二次函数①y=x2+2x,②y=x2-2x+1,③y=x2-2x+2的图象如图所示.
-1
1
-3 -2 -1
O
x
y
-1
1 2 3
y
x
O
-1
1 2 3
O
y
x
(1)每个图象与x轴有几个交点?
(2)一元二次方程x2+2x=0,x2-2x+1=0有几个根?
解方程验证一下,一元二次方程x2-2x+2=0有根吗?
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?
(2)①x1=0, x2=-2,两个不相等实数根.
②x1=x2=1,两个相等实数根.
③没有实数根.
解:(1)每个图象与x轴的交点个数分别是2个,1个,0个.
(3)二次函数y=ax2+bx+c的图象和x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
【规律方法】二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:
有两个交点、有一个交点、没有交点.
当二次函数y=ax2+bx+c的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.
例:利用二次函数的图象求方程x2-x-3=0的实数根(精确到0.1).
x
y
用你学过的一元二次方程的解法来解,
准确答案是什么?
方法: (1)先作出y=x -x-3的图象;
(2)写出交点的坐标:
(-1.3,0),(2.3,0)
(3)得出方程的解:
x1=-1.3,x2=2.3.
【例题】
C
A
【跟踪训练】
3.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴的交点
情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
C
4.根据下列表格的对应值:
判断方程ax2+bx+c=0 (a≠0,a,b,c为常数)一个解x的范围是( )
A.3
y=ax2+bx+c -0.06 -0.02 0.03 0.09
C
6.已知二次函数y=ax2+bx+c的图象如图所示,则一元二次方
程ax2+bx+c=0的解是 .
x
y
0
5
x1=0,x2=5
7.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实
数根,则m=__,此时抛物线 y=x2-2x+m与x轴有__个交
点.
8.已知抛物线 y=x2–8x+c的顶点在 x轴上,则c=__.
9.一元二次方程3x2+x-10=0的两个根是x1=-2,x2= ,
那么二次函数y=3x2+x-10与x轴的交点坐标是____和
___________.
1
1
16
( ,0)
(-2,0)
1.(崇左·中考)二次函数y=ax2+bx+c的图象如图所示,给出下列说法:①abc<0;②方程ax2+bx+c=0的根为x1=
-1,x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,-1<x<3.其中正确的说法是( )
A.① B.①②
C.①②③ D.①②③④
O
x
y
1
3
-1
答案:D
随堂练习
2.(河北·中考)如图,已知抛物线y=x2+bx+c的对称轴为x=2,点A, B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为( )
A.(2,3) B.(3,2)
C.(3,3) D.(4,3)
O
x
y
A
x = 2
B
答案:D
3.(汕头·中考)已知二次函数y=-x2+bx+c的图象如图
所示,它与x轴的一个交点坐标为(-1,0),与y轴的
交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式.
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
【解析】(1)由题意得
解得
故所求解析式为
解得
∴由图象可知,函数值y为正数时,自变量x的取值范围
是-1<x<3.
(2)令
∴抛物线与x轴的另一个交点坐标为(3,0),
4.(株洲·中考)二次函数y=x2-mx+3的图象与x轴的交点如图所示,根据图中信息可得到m的值是_______.
答案:4
5.(咸宁·中考)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)证明:4c=3b2.
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
由(1)得
∴二次函数的最小值为-4.
【解析】(1)依题意,m,-3m是一元二次方程
的两根.根据一元二次方程根与系数的
关系,得 ,
∴
,
,
(2)依题意,
,
,
,
1.二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根.
2.根据一元二次方程ax2+bx+c=0根的情况是两个不相等的实根、两个相等实根、没有实数根,图象上对应与x轴的交点个数是两个、一个、没有.
