《直接证明与间接证明》

课件24张PPT。2.2 直接证明与间接证明
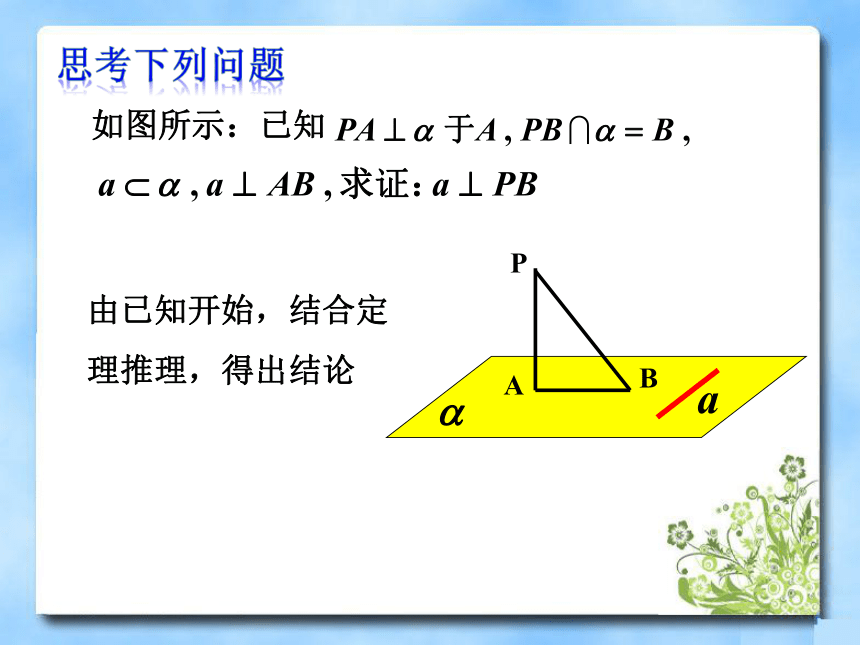
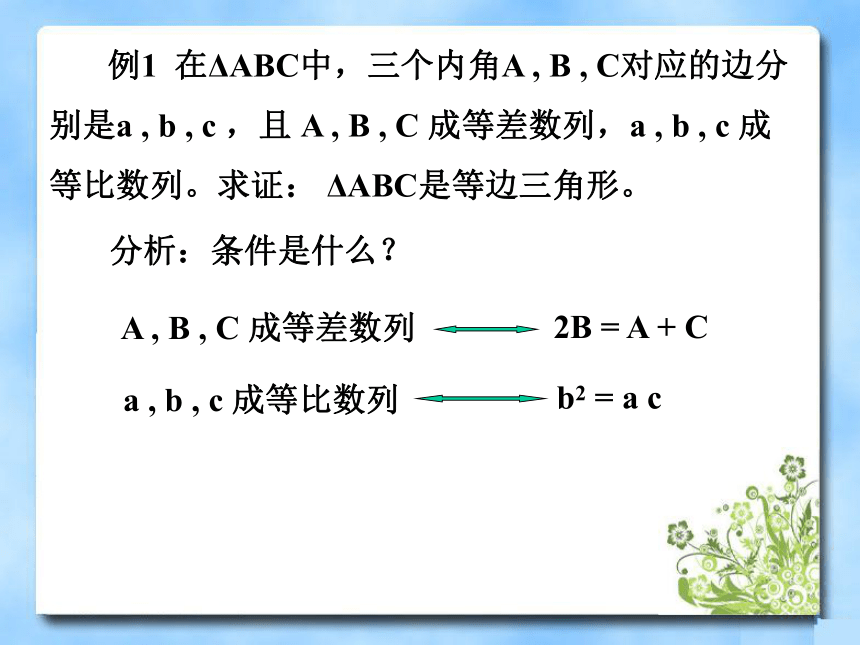
——综合法思考下列问题如图所示：已知由已知开始，结合定理推理，得出结论综合法 利用已知条件和某些数学定义、定理、公理等，经过一系列的推理论证，最后推导出所要证明的结论或所要解决的问题的结果。 例1 在ΔABC中，三个内角A , B , C对应的边分别是a , b , c ，且 A , B , C 成等差数列，a , b , c 成等比数列。求证： ΔABC是等边三角形。分析：条件是什么？例2：设 a > 0， 是 R上的偶函数。
（1）求 a 的值；
（2） 证明 f(x) 在（0，＋∞）上是增函数巩固练习2.2 直接证明与间接证明
——分析法已知 a、b、c为互不相等的正数， 温故知新探究：E为ΔABC的中线AD上任意一点?B >?C，求证：?EBC >?ECB目标：?EBC >?ECB因为 BD =DC , ED =ED因为 BD =DC , AD =AD因为 BD =DC , ED =ED因为 BD =DC , AD =AD?B >?C分析法 从结论出发，寻找结论成立的充分条件直至最后，把要证明的结论归结为判定一个明显成立的条件。要证：??
只要证：??
只需证：??
??显然成立
上述各步均可逆
所以 结论成立格 式分析法例2 设a , b , c 为一个三角形的三边长。 例1 求证：当一个圆与一个正方形的周长相等时，圆面积比正方形面积大。 例3 如图： 过A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F。求证：1、证明：
2、求证：巩固练习2.2 直接证明与间接证明
——反证法 探究2： 已知 a ≠0 ,关于 x 的方程 a x = b 有解吗？ 探究1：将9个球分别染成红色或白色无论怎样染色，至少有5个球一 定是同色的。正确吗？ 解唯一吗？反 证 法用反证法证题的一般步骤（1）假设命题的结论不成立，即假设结论的反面成立；
（2）从这个假设出发，经过推理论证,得出矛盾；
（3）由矛盾判定假设不成立，从而肯定命题的结论正确。 适宜使用反证法的情况：
（1）结论以否定形式出现
（2）结论以“至多……，”，“至少……”形式出现
（3）唯一性、存在性问题
（4）结论的反面比原结论更具体更容易研究的命题。 例1：给定实数 设函数
求证：经过函数图像上任意两个不同点的直线不平行于x轴。常见否定用语是－－不是 有－－没有
等－－不等 成立－－不成立
都是－－不都是，即至少有一个不是
都有－－不都有，即至少有一个没有
都不是－ －部分或全部是，即至少有一个是
唯一－－至少有两个
至少有一个有（是）－－全部没有（不是）
至少有一个不－－全部都方法总结：
推出矛盾，可通过特殊值进行说明。1、如果一条直线经过平面内一点，又经过平面外一点，则此直线与平面相交。2、证明：3、已知方程 2x = 3 ，求证方程有且只有一根试一试