北师大版数学七年级下册 2.1.2 垂直课件(共25张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 2.1.2 垂直课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 700.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 06:54:40 | ||
图片预览





文档简介
(共25张PPT)
第二章 相交线与平行线
1 两条直线的位置关系
第2课时 垂直
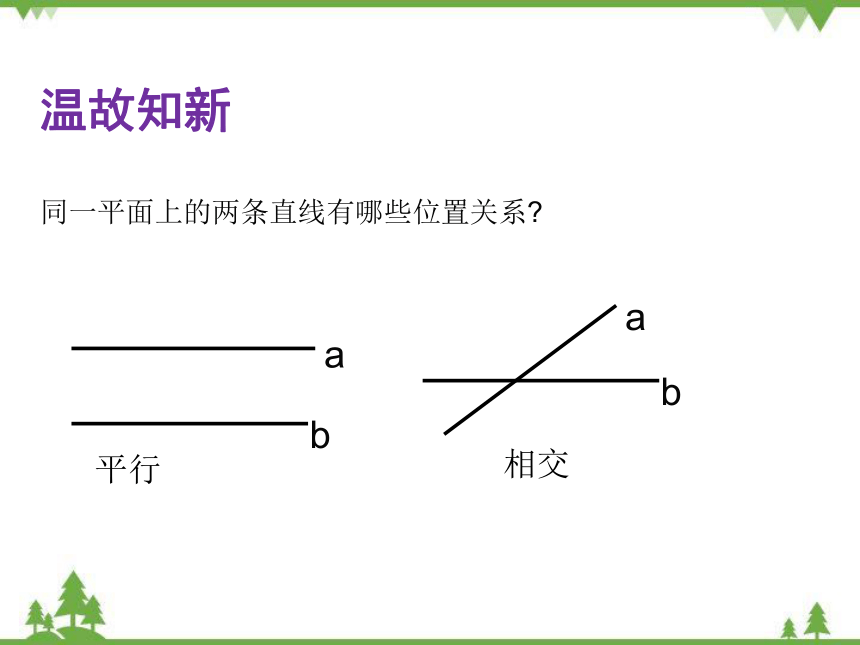
同一平面上的两条直线有哪些位置关系
a
b
平行
a
b
相交
温故知新
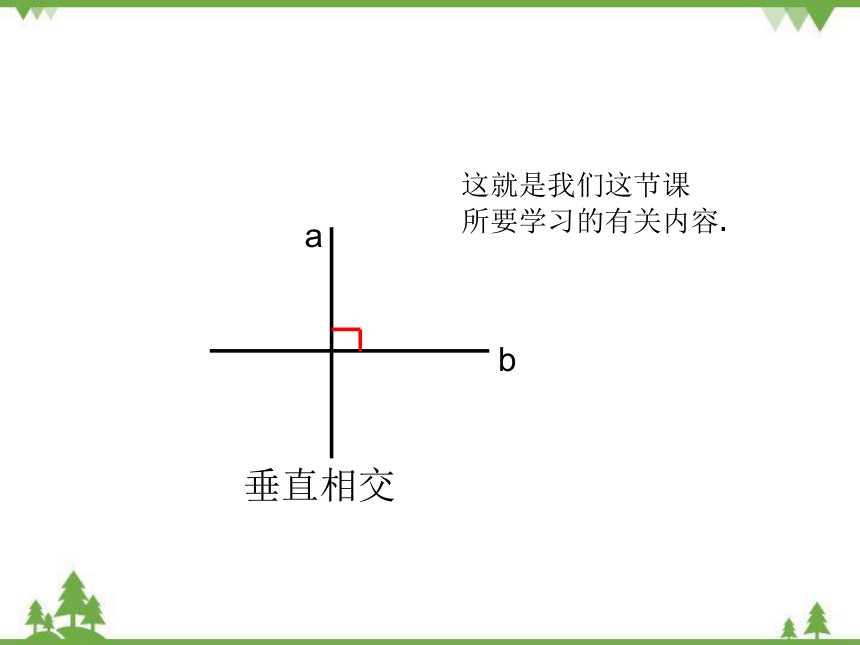
a
b
垂直相交
这就是我们这节课
所要学习的有关内容.
学习目标
1.理解垂直的定义;
2.会过一点画已知直线的垂线;
3.掌握垂线的性质并会应用;
4.理解点到直线的距离的概念.
日常生活中,两条直线互相垂直的情形很常见,说出其中的一些互相垂直的线条.
你能再举出其他例子吗
1:垂直的概念
新知探究
两条直线相交成四个角,如果有一个角
是直角,那么称这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,
它们的交点叫做垂足.
垂直的定义和表示方法
如图,AB⊥CD
垂直符号为“⊥”.
例.如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于( ).
A.30° B.34° C.45° D.56°
B
新知巩固
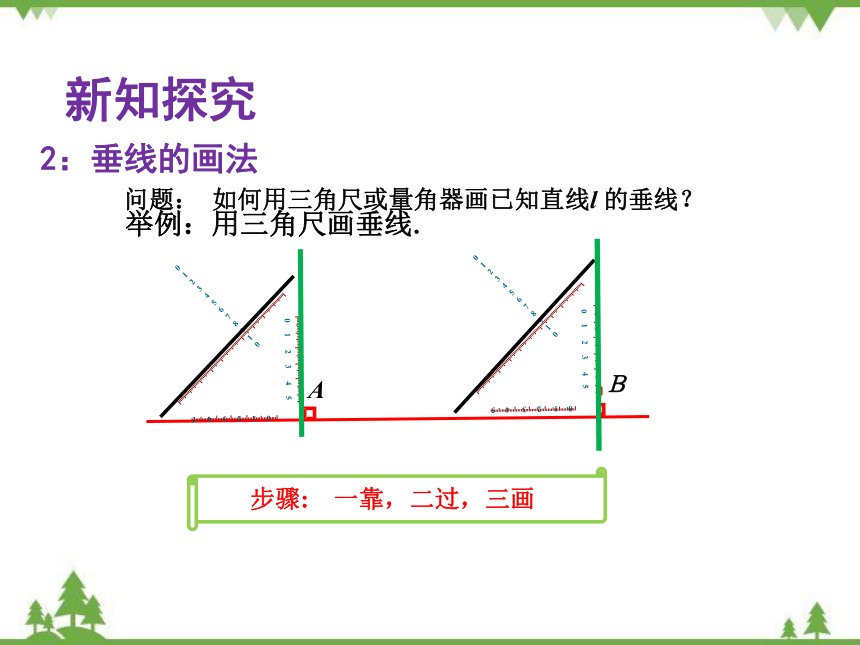
问题: 如何用三角尺或量角器画已知直线l 的垂线?
2:垂线的画法
举例:用三角尺画垂线.
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
步骤: 一靠,二过,三画
新知探究
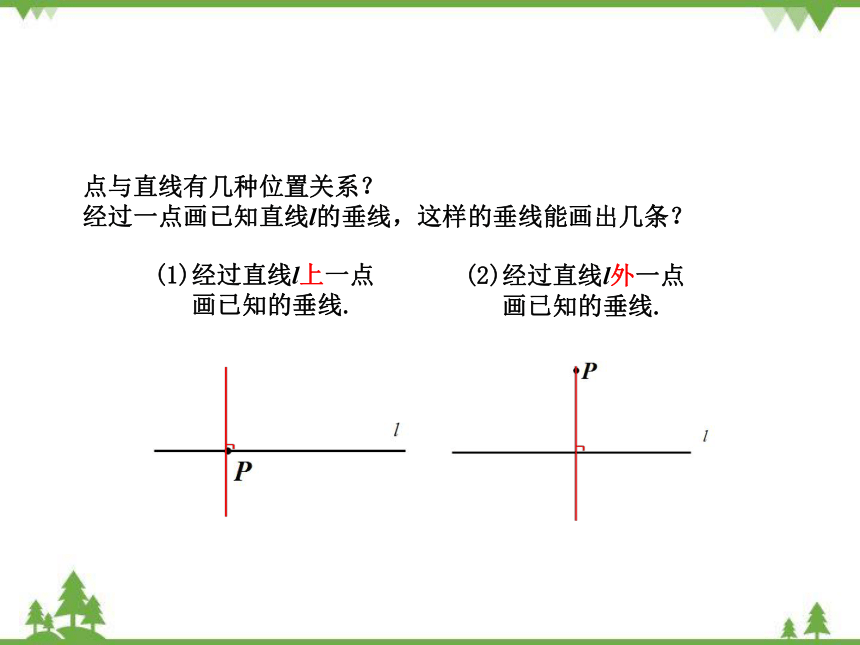
(1)经过直线l上一点
画已知的垂线.
(2)经过直线l外一点
画已知的垂线.
点与直线有几种位置关系?
经过一点画已知直线l的垂线,这样的垂线能画出几条?
结论: 平面内,过一点有且只有一条直线与已知直线垂直.(垂线的性质1)
能作一条,而且只能作一条.
问题1:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
3:垂线段的性质
新知探究
问题2: 在灌溉时,要把河中的水引到农田P处,如何
挖掘能使渠道最短?
(1)你能将这个实际问题转化成数学问题吗?
(2)在直线上有无数个点,试着取几个点与点P相
连,比较一下它们的长短,你有什么发现?
(3)你能猜想一下最短的位置会在哪儿?它唯一吗?
为什么?
(4)你能用一句话总结出观察得出的结论吗?
直线外一点与直线上各点连接的所有线段中,垂线段最短.(垂线性质2)
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
你能列举生活中类似的
实例吗?
例1 如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A 点 B.B 点 C.C 点 D.D 点
A
新知巩固
例2 下列说法中,正确的是( )
A.过直线外一点和直线上一定点可以画无数条直线与这条直线垂直
B.过直线上一点和直线外一定点可以画这条直线的垂线
C.过射线外一点可以画这条射线的一条垂线
D.如果两条直线不相交,那么这两条直线有可能互相垂直
C
1.已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
【解析】点到直线的距离是指点到直线的垂线段的长度.
课堂练习
【答案】C
2.如图,点D在直线AB上,当∠1与∠2具备条件________时,CD与AB的位置关系是垂直.
【解析】因为∠1与∠2互补,所以当∠1=∠2=90°时,CD与AB垂直.
【答案】∠1=∠2
3.如图,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF,∠BOF的度数.
解:因为∠DOF与∠COE是
对顶角,所以∠DOF=∠COE=
35°,又因为AB⊥CD,所以
∠BOD=90°,所以∠BOF=∠DOF+
∠BOD=35°+90°=125°.
E
4.如图,直线AB,CD相交于点O,OE⊥CD于O, ∠AOE:∠COE=1:3,求∠BOD的度数.
解:∵OE⊥CD
∴ ∠COE=90°
又∵∠AOE:∠COE=1:3
∴ ∠AOE= ∠COE=30°
∴ ∠COA=90°-30°=60°
∴∠BOD= ∠COA=60°
垂直的定义与表示法
垂线的画法
垂线的性质
点到直线的距离
垂直
课堂小结
过一点画已知直线的垂线的三个步骤
1.靠,让三角尺的一条直角边紧靠在已知直线上.
2.移,移动三角尺,使三角尺的另一条直角边过已知点.
3.画,沿不与已知直线重合的直角边画一直线,则该直线就是已知直线的垂线.
认识垂线及其性质的三点注意
(1)线段和射线都有垂线.
(2)点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
(3)在实际问题中,确定路径最短或最短距离问题时,首先将实际问题转化成数学问题,再作出垂线,并求出具体数值.
第二章 相交线与平行线
1 两条直线的位置关系
第2课时 垂直
同一平面上的两条直线有哪些位置关系
a
b
平行
a
b
相交
温故知新
a
b
垂直相交
这就是我们这节课
所要学习的有关内容.
学习目标
1.理解垂直的定义;
2.会过一点画已知直线的垂线;
3.掌握垂线的性质并会应用;
4.理解点到直线的距离的概念.
日常生活中,两条直线互相垂直的情形很常见,说出其中的一些互相垂直的线条.
你能再举出其他例子吗
1:垂直的概念
新知探究
两条直线相交成四个角,如果有一个角
是直角,那么称这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,
它们的交点叫做垂足.
垂直的定义和表示方法
如图,AB⊥CD
垂直符号为“⊥”.
例.如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于( ).
A.30° B.34° C.45° D.56°
B
新知巩固
问题: 如何用三角尺或量角器画已知直线l 的垂线?
2:垂线的画法
举例:用三角尺画垂线.
A
B
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
步骤: 一靠,二过,三画
新知探究
(1)经过直线l上一点
画已知的垂线.
(2)经过直线l外一点
画已知的垂线.
点与直线有几种位置关系?
经过一点画已知直线l的垂线,这样的垂线能画出几条?
结论: 平面内,过一点有且只有一条直线与已知直线垂直.(垂线的性质1)
能作一条,而且只能作一条.
问题1:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
3:垂线段的性质
新知探究
问题2: 在灌溉时,要把河中的水引到农田P处,如何
挖掘能使渠道最短?
(1)你能将这个实际问题转化成数学问题吗?
(2)在直线上有无数个点,试着取几个点与点P相
连,比较一下它们的长短,你有什么发现?
(3)你能猜想一下最短的位置会在哪儿?它唯一吗?
为什么?
(4)你能用一句话总结出观察得出的结论吗?
直线外一点与直线上各点连接的所有线段中,垂线段最短.(垂线性质2)
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
你能列举生活中类似的
实例吗?
例1 如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A 点 B.B 点 C.C 点 D.D 点
A
新知巩固
例2 下列说法中,正确的是( )
A.过直线外一点和直线上一定点可以画无数条直线与这条直线垂直
B.过直线上一点和直线外一定点可以画这条直线的垂线
C.过射线外一点可以画这条射线的一条垂线
D.如果两条直线不相交,那么这两条直线有可能互相垂直
C
1.已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
【解析】点到直线的距离是指点到直线的垂线段的长度.
课堂练习
【答案】C
2.如图,点D在直线AB上,当∠1与∠2具备条件________时,CD与AB的位置关系是垂直.
【解析】因为∠1与∠2互补,所以当∠1=∠2=90°时,CD与AB垂直.
【答案】∠1=∠2
3.如图,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF,∠BOF的度数.
解:因为∠DOF与∠COE是
对顶角,所以∠DOF=∠COE=
35°,又因为AB⊥CD,所以
∠BOD=90°,所以∠BOF=∠DOF+
∠BOD=35°+90°=125°.
E
4.如图,直线AB,CD相交于点O,OE⊥CD于O, ∠AOE:∠COE=1:3,求∠BOD的度数.
解:∵OE⊥CD
∴ ∠COE=90°
又∵∠AOE:∠COE=1:3
∴ ∠AOE= ∠COE=30°
∴ ∠COA=90°-30°=60°
∴∠BOD= ∠COA=60°
垂直的定义与表示法
垂线的画法
垂线的性质
点到直线的距离
垂直
课堂小结
过一点画已知直线的垂线的三个步骤
1.靠,让三角尺的一条直角边紧靠在已知直线上.
2.移,移动三角尺,使三角尺的另一条直角边过已知点.
3.画,沿不与已知直线重合的直角边画一直线,则该直线就是已知直线的垂线.
认识垂线及其性质的三点注意
(1)线段和射线都有垂线.
(2)点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
(3)在实际问题中,确定路径最短或最短距离问题时,首先将实际问题转化成数学问题,再作出垂线,并求出具体数值.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
