数学高中苏教版选修(2-3)2.2《超几何分布》课件
文档属性
| 名称 | 数学高中苏教版选修(2-3)2.2《超几何分布》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-02 16:21:07 | ||
图片预览




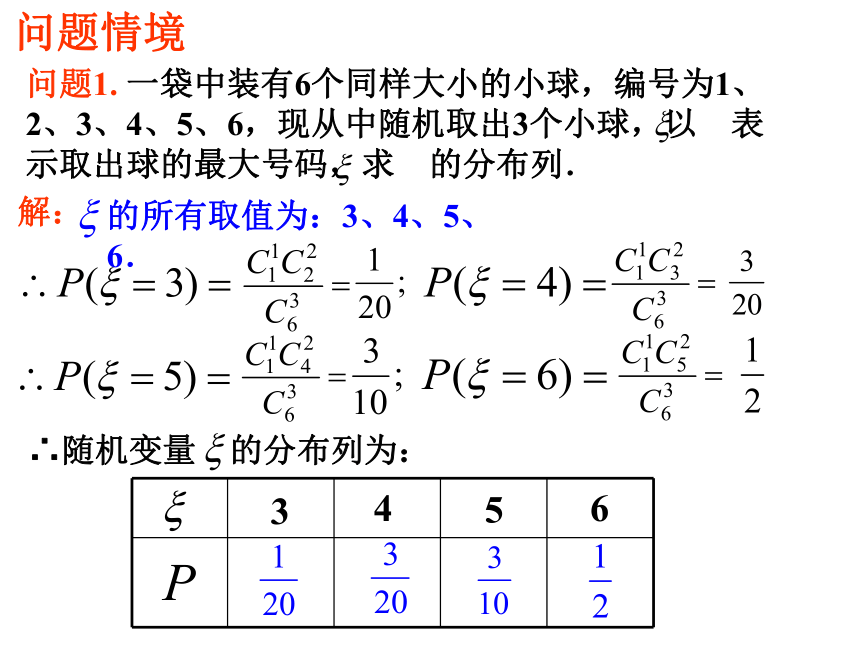



文档简介
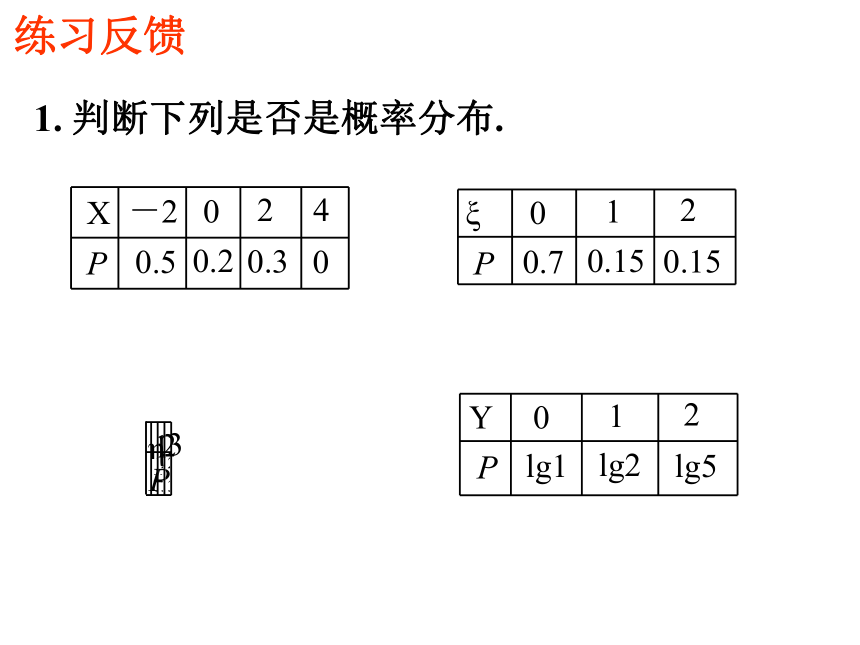
课件22张PPT。热烈欢迎各位专家指导!知识回顾2. 随机变量的概率分布设随机变量 X 有n个不同的取值则称上式为随机变量 X 的概率分布列.1. 随机变量 如果随机试验的结果可以用一个变量来表示,那么这样的变量叫随机变量.称为随机变量 X 的概率分布表.概率分布3. 随机变量概率分布的性质:知识回顾1. 判断下列是否是概率分布.练习反馈2. 在掷一枚图钉的随机试验中,令如果针尖向上的概率为p,试写出随机变量 X 的概率分布.解:根据分布列的性质,针尖向下的概率是(1-p),于是,随机变量X的概率分布是:两点分布列;X~0-1分布;X~ 两点分布练习反馈问题情境解:6543问题2.一批产品有 10 件,其中有 5 件次品.现
从中取出 5 件.令 X:取出5 件产品中的次品
数. 则 X 的概率分布为:问题情境思考:我们可不可以把上面的问题推广到一般情况呢?一批产品有N件,其中有M 件次品.现从中取出
n 件.令 X:取出 n 件产品中的次品数.
则 X 的分布列为数学建构2.2 超几何分布兴化市楚水实验学校高二数学备课组数学概念记为:X~H(n,M,N), 一般地,若一个随机变量X的分布列为:1. 超几何分布定义:称分布列为超几何分布数学概念注意:(1) 超几何分布的模型是不放回抽样.(2) 超几何分中的参数是M, N, n.(3) 记号H(r;n,M,N)中字母的含义.H(r; n, M, N)样本容量样本中不合格品数不合格品总数总体中的个体总数数学运用解:用随机变量X表示取到的红球数,则X服从超几何分
布H(5,10,30). 则:答:获一等奖的概率约为2.95%.例1 高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有10个红球、20个白球,这些球除颜色外完全相同,一次从中摸出5个球,摸到4个红球1个白球的就获一等奖. 求获得一等奖的概率.变题:至少摸出4个红球就中一等奖?本题中X的概率分布如下:数学运用例1 高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有10个红球、20个白球,这些球除颜色外完全相同,一次从中摸出5个球,摸到4个红球1个白球的就获一等奖. 求获得一等奖的概率.解:用X表示“5箱中不合格产品的箱数”,则X服从超几何分布 H(5,2,50). 则这批产品被接受的条件是 5 箱中没有不合格产品或只有1箱不合格产品,所以被接受的概率为P(X≤1),即:答:该批产品被接受的概率约为0.99184.数学运用例2 生产方提供50箱的一批产品,其中2箱不合格产品. 采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,则接收该批产品. 问:该批产品被接收的概率是多少?例3 盒中装有一打(12个)乒乓球,其中9个是新的,3个旧的 (用过的球即为旧的) ,从盒中任取3个来用,用完装回盒中,此时盒中旧球个数X是一个随机变量,求X的概率分布.数学运用解: 从盒中任取3个.这3个可能全是旧的,2个旧的1个新的, 1个旧的2个新的或全是新的.所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即X可以取3,4,5,6.例3 盒中装有一打(12个)乒乓球,其中9个是新的,3个旧的 (用过的球即为旧的) ,从盒中任取3个来用,用完装回盒中,此时盒中旧球个数X是一个随机变量,求X的概率分布.数学运用所以X的概率分布列为:例4 在一次英语口语考试中,有备选的10道试题,已知某考生能答对其中的8道试题,规定每次考试都从备选题中任选3道题进行测试,至少答对2道题才算合格,求该考生答对试题数X的分布列,并求该考生及格的概率.数学运用从全班任取n个人,取到女生的人数;
从扑克牌中取n张,取到黑桃的张数;
买n张彩票,中奖的张数……
等等都可以用超几何分布描述. 超几何分布问题类型:思考总结:课堂练习课本P51 练习1,2课堂小结记为:X~H(n,M,N), 一般地,若一个随机变量X的分布列为:超几何分布:称分布列为超几何分布布置作业超几何分布课时作业谢谢指导!
从中取出 5 件.令 X:取出5 件产品中的次品
数. 则 X 的概率分布为:问题情境思考:我们可不可以把上面的问题推广到一般情况呢?一批产品有N件,其中有M 件次品.现从中取出
n 件.令 X:取出 n 件产品中的次品数.
则 X 的分布列为数学建构2.2 超几何分布兴化市楚水实验学校高二数学备课组数学概念记为:X~H(n,M,N), 一般地,若一个随机变量X的分布列为:1. 超几何分布定义:称分布列为超几何分布数学概念注意:(1) 超几何分布的模型是不放回抽样.(2) 超几何分中的参数是M, N, n.(3) 记号H(r;n,M,N)中字母的含义.H(r; n, M, N)样本容量样本中不合格品数不合格品总数总体中的个体总数数学运用解:用随机变量X表示取到的红球数,则X服从超几何分
布H(5,10,30). 则:答:获一等奖的概率约为2.95%.例1 高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有10个红球、20个白球,这些球除颜色外完全相同,一次从中摸出5个球,摸到4个红球1个白球的就获一等奖. 求获得一等奖的概率.变题:至少摸出4个红球就中一等奖?本题中X的概率分布如下:数学运用例1 高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有10个红球、20个白球,这些球除颜色外完全相同,一次从中摸出5个球,摸到4个红球1个白球的就获一等奖. 求获得一等奖的概率.解:用X表示“5箱中不合格产品的箱数”,则X服从超几何分布 H(5,2,50). 则这批产品被接受的条件是 5 箱中没有不合格产品或只有1箱不合格产品,所以被接受的概率为P(X≤1),即:答:该批产品被接受的概率约为0.99184.数学运用例2 生产方提供50箱的一批产品,其中2箱不合格产品. 采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,则接收该批产品. 问:该批产品被接收的概率是多少?例3 盒中装有一打(12个)乒乓球,其中9个是新的,3个旧的 (用过的球即为旧的) ,从盒中任取3个来用,用完装回盒中,此时盒中旧球个数X是一个随机变量,求X的概率分布.数学运用解: 从盒中任取3个.这3个可能全是旧的,2个旧的1个新的, 1个旧的2个新的或全是新的.所以用完放回盒中,盒中旧球个数可能是3个,4个,5个,6个,即X可以取3,4,5,6.例3 盒中装有一打(12个)乒乓球,其中9个是新的,3个旧的 (用过的球即为旧的) ,从盒中任取3个来用,用完装回盒中,此时盒中旧球个数X是一个随机变量,求X的概率分布.数学运用所以X的概率分布列为:例4 在一次英语口语考试中,有备选的10道试题,已知某考生能答对其中的8道试题,规定每次考试都从备选题中任选3道题进行测试,至少答对2道题才算合格,求该考生答对试题数X的分布列,并求该考生及格的概率.数学运用从全班任取n个人,取到女生的人数;
从扑克牌中取n张,取到黑桃的张数;
买n张彩票,中奖的张数……
等等都可以用超几何分布描述. 超几何分布问题类型:思考总结:课堂练习课本P51 练习1,2课堂小结记为:X~H(n,M,N), 一般地,若一个随机变量X的分布列为:超几何分布:称分布列为超几何分布布置作业超几何分布课时作业谢谢指导!
