2.3一元二次不等式及其解法 课件(共14张PPT)
文档属性
| 名称 | 2.3一元二次不等式及其解法 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 740.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
一元二次不等式的解法(3)
含待定系数的不等式
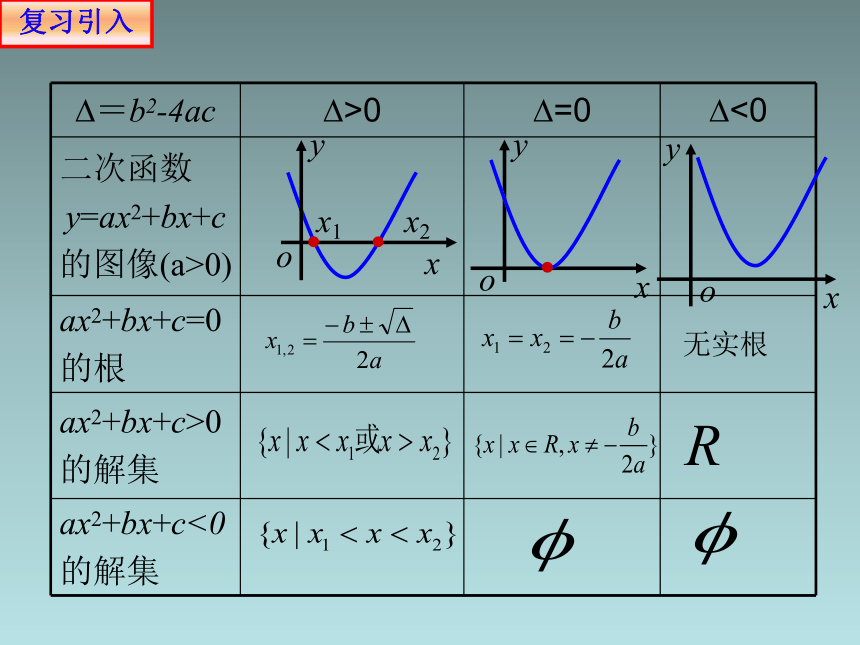
=b2-4ac >0 =0 <0
二次函数
y=ax2+bx+c
的图像(a>0)
ax2+bx+c=0
的根
ax2+bx+c>0
的解集
ax2+bx+c<0
的解集
x
y
o
x
y
o
●
x
y
o
x1
x2
●
●
无实根
复习引入
1.不等式(x2-7x+12)(x2+x+1)>0的解集为 ( )
A.(-∞,-4)∪(-3,+∞)
B.(-∞,3)∪(4,+∞)
C.(-4,-3)
D.(3,4)
解析:∵x2+x+1>0恒成立,∴原不等式等价于x2-7x+12>0,∴x<3或x>4.故选B.
答案:B
复习练习
[例1] 设A={x|x2-(a+a2)x+a3<0},
B={x|x2-3x+2<0},若A∩B=A,
求实数a的取值范围.
[分析] 由A∩B=A A B,又因为B是可解集合,因此可以求出B集合.对于A集合,要明确不等式的解集,需判断对应方程两根的大小,故要就两根的大小对参数a加以讨论,再借助数轴由A,B两集合的关系,求出a的具体取值范围.
典型例题
[解] 因为A∩B=A,所以A B.
B={x|x2-3x+2<0}={x|1因为x2-(a+a2)x+a3=(x-a2)(x-a)<0,
所以x介于a与a2之间.
当a1或a<0时,A={x|a若A B,则需满足 如图1所示,
已知集合A={x|x2-x-6>0},B={x|0解:由x2-x-6>0,得(x-3)(x+2)>0,
∴x<-2或x>3. ∴A={x|x<-2或x>3}.
由0∴B={x|-a又∵A∩B= ,
∴ 解得1≤a≤2.
故所求实数a的取值范围为{a|1≤a≤2}.
练习巩固
[例2] 汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析交通事故的一个重要因素.在一个限速40 km/h的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是发生了轻微碰撞.事发后现场勘查测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间分别有如下关系:
s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.
试判断甲、乙两车有无超速现象,并根据所学数学知识给出判断的依据.
典型例题
[分析] 由题目可获取以下主要信息:
①限速40 km/h;②刹车距离s甲>12 m,s乙>10 m;
③刹车距离s甲、s乙与车速关系确定.
解答本题可将刹车距离直接代入关系式分别得到一个关于x的一元二次不等式,解此不等式即可求出x的范围,即汽车刹车前的车速范围.
[解] 由题意,对于甲车,有0.1x+0.01x2>12,
即x2+10x-1200>0.
解得x>30或x<-40(舍去).
这表明甲车的车速超过30 km/h,但根据题意刹车距离略超过12 m,由此估计甲车不会超过限速40 km/h.
对于乙车,有0.05x+0.005x2>10,
即x2+10x-2000>0.
解得x>40或x<-50(舍去).
这表明乙车的车速超过40 km/h,超过规定限速.
典型例题
[点评] (1)实际应用问题是新课标下考查的重点,突出了应用能力的考查,在不等式应用题中常以函数模型出现,如一元二次不等式应用题常以二次函数为模型.解题时要弄清题意,准确找出其中不等关系再利用不等式解法求解.
(2)解不等式应用题,一般可按如下四步进行:
①阅读理解、认真审题、把握问题中的关键量、找准不等关系;
②引进数学符号,用不等式表示不等关系(或表示成函数关系);
③解不等式(或求函数最值);
④回扣实际问题.
某企业上年度的年利润为200万元,本年度为适应市场需求,计划提高产品档次,适度增加投入成本,投入成本增加的比例为x(0巩固练习
1.一元二次不等式的解题步骤可总结为:
首先化为标准形式ax2+bx+c>0或ax2+bx+c<0,其中a>0,然后解出相应的一元二次方程的根,再结合二次函数的图象便可得出解集.一般步骤为:一看(看二次项系数a的正负);二算(计算判别式,判断相应方程根的情况并求根);三写(写出不等式的解集).
课堂小结
2.从函数观点看:一元二次不等式ax2+bx+c>0(a>0)的解集,即二次函数y=ax2+bx+c(a>0)的值满足y>0时的自变量x组成的集合,即二次函数y=ax2+bx+c(a>0)的图象在x轴上方时点的横坐标x的集合,而一元二次方程ax2+bx+c=0(a>0)的根就是二次函数图象与x轴交点的横坐标,因此要加深理解“一元二次函数、一元二次方程和一元二次不等式”这三个“二次” 之间的内在联系.
3.一元一次不等式(组)和一元二次不等式(组)的解法是不等式的基础,因为很多不等式的求解最终都是转化为一元一次不等式(组)和一元二次不等式(组)进行.
一元二次不等式的解法(3)
含待定系数的不等式
=b2-4ac >0 =0 <0
二次函数
y=ax2+bx+c
的图像(a>0)
ax2+bx+c=0
的根
ax2+bx+c>0
的解集
ax2+bx+c<0
的解集
x
y
o
x
y
o
●
x
y
o
x1
x2
●
●
无实根
复习引入
1.不等式(x2-7x+12)(x2+x+1)>0的解集为 ( )
A.(-∞,-4)∪(-3,+∞)
B.(-∞,3)∪(4,+∞)
C.(-4,-3)
D.(3,4)
解析:∵x2+x+1>0恒成立,∴原不等式等价于x2-7x+12>0,∴x<3或x>4.故选B.
答案:B
复习练习
[例1] 设A={x|x2-(a+a2)x+a3<0},
B={x|x2-3x+2<0},若A∩B=A,
求实数a的取值范围.
[分析] 由A∩B=A A B,又因为B是可解集合,因此可以求出B集合.对于A集合,要明确不等式的解集,需判断对应方程两根的大小,故要就两根的大小对参数a加以讨论,再借助数轴由A,B两集合的关系,求出a的具体取值范围.
典型例题
[解] 因为A∩B=A,所以A B.
B={x|x2-3x+2<0}={x|1
所以x介于a与a2之间.
当a
已知集合A={x|x2-x-6>0},B={x|0
∴x<-2或x>3. ∴A={x|x<-2或x>3}.
由0
∴ 解得1≤a≤2.
故所求实数a的取值范围为{a|1≤a≤2}.
练习巩固
[例2] 汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”.刹车距离是分析交通事故的一个重要因素.在一个限速40 km/h的弯道上,甲、乙两车相向而行,发现情况不对,同时刹车,但还是发生了轻微碰撞.事发后现场勘查测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间分别有如下关系:
s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.
试判断甲、乙两车有无超速现象,并根据所学数学知识给出判断的依据.
典型例题
[分析] 由题目可获取以下主要信息:
①限速40 km/h;②刹车距离s甲>12 m,s乙>10 m;
③刹车距离s甲、s乙与车速关系确定.
解答本题可将刹车距离直接代入关系式分别得到一个关于x的一元二次不等式,解此不等式即可求出x的范围,即汽车刹车前的车速范围.
[解] 由题意,对于甲车,有0.1x+0.01x2>12,
即x2+10x-1200>0.
解得x>30或x<-40(舍去).
这表明甲车的车速超过30 km/h,但根据题意刹车距离略超过12 m,由此估计甲车不会超过限速40 km/h.
对于乙车,有0.05x+0.005x2>10,
即x2+10x-2000>0.
解得x>40或x<-50(舍去).
这表明乙车的车速超过40 km/h,超过规定限速.
典型例题
[点评] (1)实际应用问题是新课标下考查的重点,突出了应用能力的考查,在不等式应用题中常以函数模型出现,如一元二次不等式应用题常以二次函数为模型.解题时要弄清题意,准确找出其中不等关系再利用不等式解法求解.
(2)解不等式应用题,一般可按如下四步进行:
①阅读理解、认真审题、把握问题中的关键量、找准不等关系;
②引进数学符号,用不等式表示不等关系(或表示成函数关系);
③解不等式(或求函数最值);
④回扣实际问题.
某企业上年度的年利润为200万元,本年度为适应市场需求,计划提高产品档次,适度增加投入成本,投入成本增加的比例为x(0
1.一元二次不等式的解题步骤可总结为:
首先化为标准形式ax2+bx+c>0或ax2+bx+c<0,其中a>0,然后解出相应的一元二次方程的根,再结合二次函数的图象便可得出解集.一般步骤为:一看(看二次项系数a的正负);二算(计算判别式,判断相应方程根的情况并求根);三写(写出不等式的解集).
课堂小结
2.从函数观点看:一元二次不等式ax2+bx+c>0(a>0)的解集,即二次函数y=ax2+bx+c(a>0)的值满足y>0时的自变量x组成的集合,即二次函数y=ax2+bx+c(a>0)的图象在x轴上方时点的横坐标x的集合,而一元二次方程ax2+bx+c=0(a>0)的根就是二次函数图象与x轴交点的横坐标,因此要加深理解“一元二次函数、一元二次方程和一元二次不等式”这三个“二次” 之间的内在联系.
3.一元一次不等式(组)和一元二次不等式(组)的解法是不等式的基础,因为很多不等式的求解最终都是转化为一元一次不等式(组)和一元二次不等式(组)进行.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
