数学高中苏教版选修(2-3)3.2《回归分析》课件
文档属性
| 名称 | 数学高中苏教版选修(2-3)3.2《回归分析》课件 | 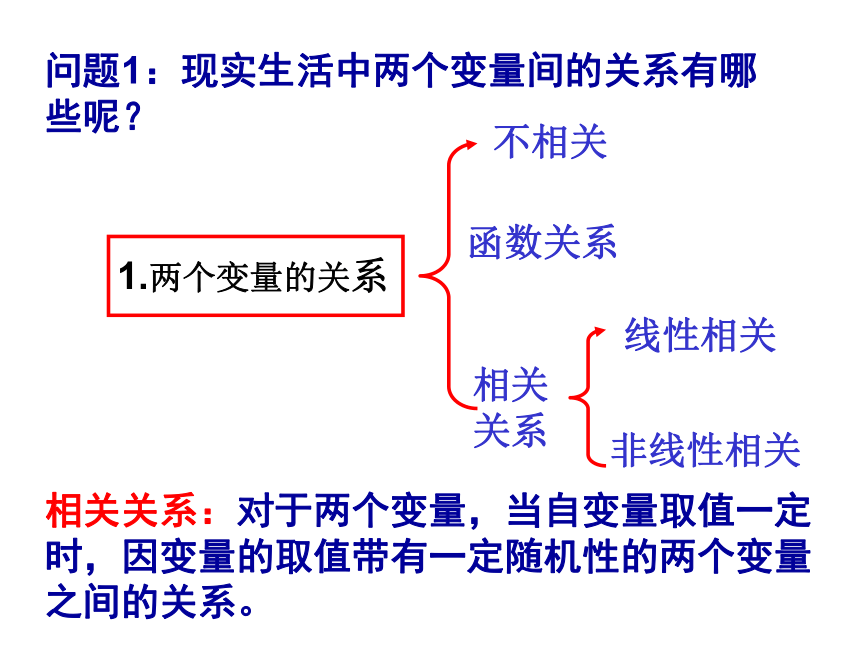 | |
| 格式 | zip | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-02 16:21:07 | ||
图片预览






文档简介
课件15张PPT。1.两个变量的关系不相关相关关系函数关系线性相关非线性相关问题1:现实生活中两个变量间的关系有哪些呢?相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。问题2:对于线性相关的两个变量用什么方法来刻划它们之间的关系呢?2、最小二乘估计最小二乘估计下的线性回归方程:3、回归分析的基本步骤:画散点图求回归方程预报、决策
画散点图
求出 , 的值。
求回归直线方程
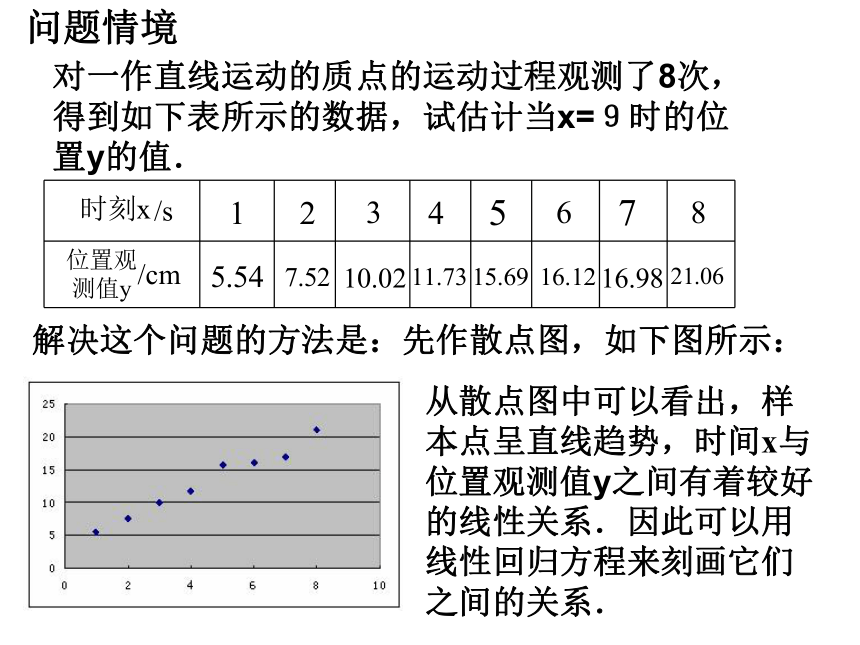
用回归直线方程解决应用问题对一作直线运动的质点的运动过程观测了8次,得到如下表所示的数据,试估计当x=9时的位置y的值.问题情境解决这个问题的方法是:先作散点图,如下图所示:从散点图中可以看出,样本点呈直线趋势,时间x与位置观测值y之间有着较好的线性关系.因此可以用线性回归方程来刻画它们之间的关系.根据线性回归的系数公式:
可以得到线性回归方程为所以当时,由线性回归方程可以估计其位置值为§3.2回归分析(1)学习目标:通过对典型案例的探究,进一步了解回归的基本思想、方法、及初步应用。自学指导:
1.“质点运动”的散点图如何作出?其回归系数如何确定?
2.什么叫随机误差?随机误差产生的原因有哪几种?
3.什么叫线性回归模型?应注意哪两点?
4.相关关系与函数关系有怎样的不同?
5.对于线性相关的两个变量用什么方法来刻划它们之间的关系呢?自学检测:P104、练习11.线性回归模型其中a+bx是确定性函数, ? 是随机误差.注:? 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差。注意:(2) 在模型合理的情况下,如何估计a,b.(1) 模型的合理性;2.探求线性回归系数的最佳估计值:对应的随机误差项我们希望总误差越小越好,即要使越小越好.故只要求出使,.,回归直线,此直线方程即为线性回归方程.其中称为回归系数,称为回归值.例1.下表给出我国从1949至1999年人口数
据资料,试根据表中数据估计我国2004年
的人口数。分析:先画图解:作出11个点(x,y)构成的散点图, 由图可知,这些点在一条直线附近,可以用线性回归模型来表示它们之间的关系. 根据公式(1)可得因此线性回归方程为即2004年的人口总数估计为13.23亿.时,分层训练: 必做题:P104、练习2(2) 选做题:P108、复习题2(2),(3)作业:P106 习题3.2、2问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?请看下节课分解
画散点图
求出 , 的值。
求回归直线方程
用回归直线方程解决应用问题对一作直线运动的质点的运动过程观测了8次,得到如下表所示的数据,试估计当x=9时的位置y的值.问题情境解决这个问题的方法是:先作散点图,如下图所示:从散点图中可以看出,样本点呈直线趋势,时间x与位置观测值y之间有着较好的线性关系.因此可以用线性回归方程来刻画它们之间的关系.根据线性回归的系数公式:
可以得到线性回归方程为所以当时,由线性回归方程可以估计其位置值为§3.2回归分析(1)学习目标:通过对典型案例的探究,进一步了解回归的基本思想、方法、及初步应用。自学指导:
1.“质点运动”的散点图如何作出?其回归系数如何确定?
2.什么叫随机误差?随机误差产生的原因有哪几种?
3.什么叫线性回归模型?应注意哪两点?
4.相关关系与函数关系有怎样的不同?
5.对于线性相关的两个变量用什么方法来刻划它们之间的关系呢?自学检测:P104、练习11.线性回归模型其中a+bx是确定性函数, ? 是随机误差.注:? 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差。注意:(2) 在模型合理的情况下,如何估计a,b.(1) 模型的合理性;2.探求线性回归系数的最佳估计值:对应的随机误差项我们希望总误差越小越好,即要使越小越好.故只要求出使,.,回归直线,此直线方程即为线性回归方程.其中称为回归系数,称为回归值.例1.下表给出我国从1949至1999年人口数
据资料,试根据表中数据估计我国2004年
的人口数。分析:先画图解:作出11个点(x,y)构成的散点图, 由图可知,这些点在一条直线附近,可以用线性回归模型来表示它们之间的关系. 根据公式(1)可得因此线性回归方程为即2004年的人口总数估计为13.23亿.时,分层训练: 必做题:P104、练习2(2) 选做题:P108、复习题2(2),(3)作业:P106 习题3.2、2问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?请看下节课分解
