数学高中苏教版选修(2-3)1.2《排列》课件2
文档属性
| 名称 | 数学高中苏教版选修(2-3)1.2《排列》课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 585.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-02 00:00:00 | ||
图片预览





文档简介
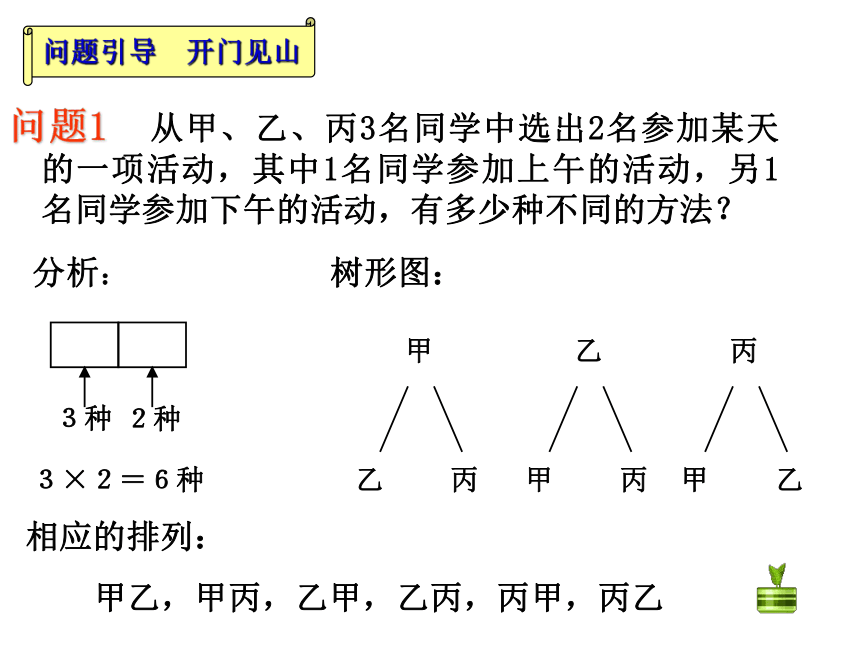
课件16张PPT。1.2 排列(一)问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的方法?
问题引导 开门见山3×2=6种甲乙丙分析:树形图:相应的排列:甲乙,甲丙,乙甲,乙丙,丙甲,丙乙问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法?
把问题1中被取的对象叫做元素
问题改述为:
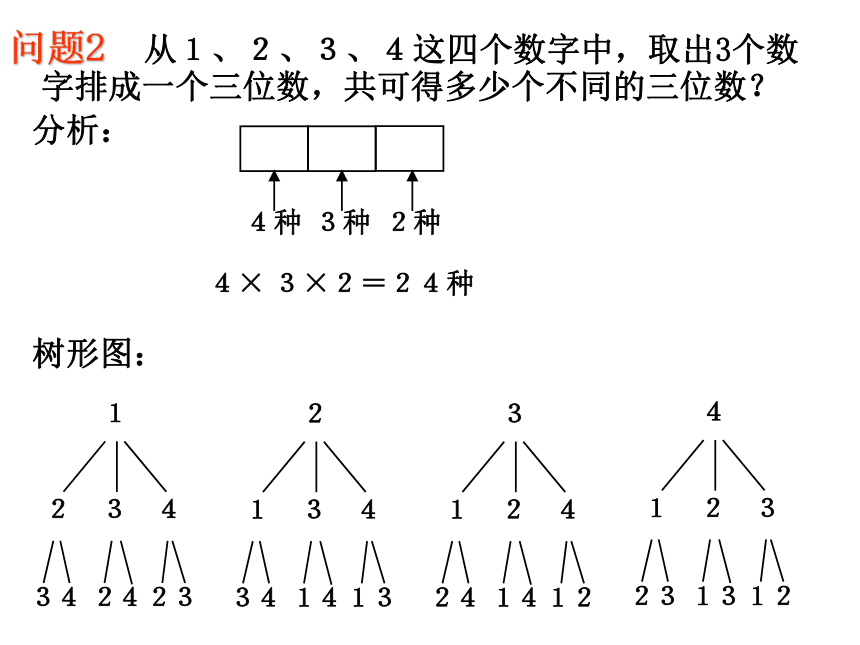
从3个不同的元素a,b,c中任取2个,按照一定的顺序排成一列,共有多少种不同的排列方法。不同的排列为:ab ac ba bc ca cb 共有 3X2=6 种4× 3×2=24种问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数? 分析:1树形图:问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
把问题1中被取的对象叫做元素
问题改述为: 从4个不同的元素a,b,c,d中任取3个,按照一定的顺序排成一列,共有多少种不同的排列方法。不同的排列为:
abc abd acb acd adb adc
bac bad bca bcd bda bdc
cab cad cba cbd cda cdb
dab dac dba dbc dca dcb共有 4X3X2=24 种2 排列的定义一般地说,从 n 个不同元素中,任取 m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列. 注意:(2)排列包括两个方面:(4)两个排列相同的充要条件:元素相同,
且顺序相同取→排(3)n个元素不同,m个元素不同(1) 且 m≤n理论迁移 例1 判断下列“事情”是否为排列:是是是否(2)从全班50名同学中挑选4人;(3)从某6人中选取4人参加4×100m接力赛;(4)将3本不同的书分发给3个人.(1)5人站成一排照相;练习1 下列问题是排列问题吗?(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条射线?可确定多少条直线?
(5)10个学生排队照相,则不同的站法有多少种?是排列不是排列是排列是排列不是排列是排列3 排列数的定义从 n 个不同元素中,任取 m (m≤n) 个元素的所有不同的排列的个数,叫做从 n 个不同元素中取出 m 个元素的一个排列数. 记作注意:(2)排列与排列数的区别排 列:不是数 ,
是有序的元素列排列数:是数 ,排列的个数(1) 且 m≤n问题3 从n个不同元素中取出2个元素,排成一列,共有多少种排列方法?问题4 从n个不同元素中取出3个元素,排成一列,共有多少种排列方法?合作交流 互动探究问题5 从n个不同元素中取出m个元素,排成一列,共有多少种排列方法?合作交流 互动探究 排列数公式:排列数公式的特征:
(1)m项相乘;
(2)右边第一个因数是n ,后面每个因数比前一个少1表示什么?n个元素全部取出的排列的个数,其中每个排列叫做n 个元素的一个全排列(n的阶乘)规定: 例2 某年全国足球甲级(A组)联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,求总共要进行多少场比赛.例3(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法? (2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法? 小结:【排列】从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列.
【关键点】1、互异性(被选、所选元素互不相同)
2、有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列总数练习1:写出从a、b、c、d四个元素中任取2个元素的所有排列,并计算其排列数。1714练习提高 巩固成果
问题引导 开门见山3×2=6种甲乙丙分析:树形图:相应的排列:甲乙,甲丙,乙甲,乙丙,丙甲,丙乙问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,1名同学参加下午的活动,有多少种不同的方法?
把问题1中被取的对象叫做元素
问题改述为:
从3个不同的元素a,b,c中任取2个,按照一定的顺序排成一列,共有多少种不同的排列方法。不同的排列为:ab ac ba bc ca cb 共有 3X2=6 种4× 3×2=24种问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数? 分析:1树形图:问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
把问题1中被取的对象叫做元素
问题改述为: 从4个不同的元素a,b,c,d中任取3个,按照一定的顺序排成一列,共有多少种不同的排列方法。不同的排列为:
abc abd acb acd adb adc
bac bad bca bcd bda bdc
cab cad cba cbd cda cdb
dab dac dba dbc dca dcb共有 4X3X2=24 种2 排列的定义一般地说,从 n 个不同元素中,任取 m (m≤n) 个元素,按照一定的顺序排成一列,叫做从 n 个不同元素中取出 m 个元素的一个排列. 注意:(2)排列包括两个方面:(4)两个排列相同的充要条件:元素相同,
且顺序相同取→排(3)n个元素不同,m个元素不同(1) 且 m≤n理论迁移 例1 判断下列“事情”是否为排列:是是是否(2)从全班50名同学中挑选4人;(3)从某6人中选取4人参加4×100m接力赛;(4)将3本不同的书分发给3个人.(1)5人站成一排照相;练习1 下列问题是排列问题吗?(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)从1到10十个自然数中任取两个组成点的坐标,可得多少个不同的点的坐标?
(4)平面上有5个点,任意三点不共线,这五点最多可确定多少条射线?可确定多少条直线?
(5)10个学生排队照相,则不同的站法有多少种?是排列不是排列是排列是排列不是排列是排列3 排列数的定义从 n 个不同元素中,任取 m (m≤n) 个元素的所有不同的排列的个数,叫做从 n 个不同元素中取出 m 个元素的一个排列数. 记作注意:(2)排列与排列数的区别排 列:不是数 ,
是有序的元素列排列数:是数 ,排列的个数(1) 且 m≤n问题3 从n个不同元素中取出2个元素,排成一列,共有多少种排列方法?问题4 从n个不同元素中取出3个元素,排成一列,共有多少种排列方法?合作交流 互动探究问题5 从n个不同元素中取出m个元素,排成一列,共有多少种排列方法?合作交流 互动探究 排列数公式:排列数公式的特征:
(1)m项相乘;
(2)右边第一个因数是n ,后面每个因数比前一个少1表示什么?n个元素全部取出的排列的个数,其中每个排列叫做n 个元素的一个全排列(n的阶乘)规定: 例2 某年全国足球甲级(A组)联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,求总共要进行多少场比赛.例3(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法? (2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法? 小结:【排列】从n个不同元素中选出m(m≤n)个元素,并按一定的顺序排成一列.
【关键点】1、互异性(被选、所选元素互不相同)
2、有序性(所选元素有先后位置等顺序之分)
【排列数】所有排列总数练习1:写出从a、b、c、d四个元素中任取2个元素的所有排列,并计算其排列数。1714练习提高 巩固成果
