人教版高中数学新教材必修第一册课件:4.2.1指数函数的概念 (共22张PPT)
文档属性
| 名称 | 人教版高中数学新教材必修第一册课件:4.2.1指数函数的概念 (共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 08:55:02 | ||
图片预览







文档简介
(共22张PPT)
4.2.1指数函数的概念
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放1粒,第2格放2粒,第3格放4粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。国王马上派人搬来麦粒开始摆放,但很快他发现这个要求根本不可能满足,因为所有麦粒的总和是个天文数字。
到底需要多少粒小麦呢?这是一个20位数,一个天文数字。这个数字的小麦折算成重量,约为2587亿吨。即使现在,全世界小麦年产量也达不到这个数字。有人说,用80立方米的仓库存放这些小麦,把这些仓库连接起来,可以从地球一直延伸到太阳。
新课引入
新课引入
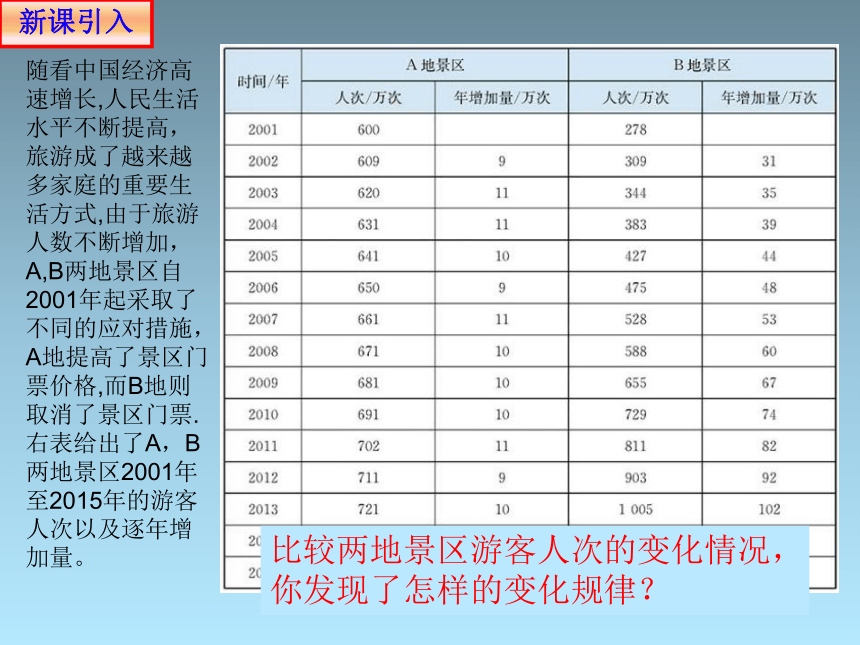
随看中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式,由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票.右表给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量。
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
新课引入
为了有利于观察规律,根据表格,分别画出A,B两地景区采取不同措施后的15年游客人次的图象
观察图象和表格,可以发现,A地景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为10万次);B地景区的游客人次则是非线性增长,年增加量越来越大,但从图象和年增加量都难以看出变化规律.
新课引入
结果表明,B地景区的游客人次的年增长率都约为
1.11-1=0.11,是一个常数。
像这样,增长率为常数的变化方式,我们称为指数增长.因此,B地景区的游客人次近似于指数增长.
显然,从2001年开始,B地景区游客人次的变化规律以近似描述为:
从2002年起,将B地景区每年的游客人次除以上一年的游客人次,可以得到
…………
1年后,游客人次是2001年的1.111倍;
2年后,游客人次是2001年的1.112倍;
3年后,游客人次是2001年的1.113倍;
...x年后,游客人次是2001年的1.11x倍。
如果设经过x年后的游客人次为2001年的y倍,
那么y=1.11x(x∈[0,+∞)这是一个函数,其中指数x是自变量。
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达为
表达式
新课引入
比较下列指数的异同,
若是函数值?是什么函数?
①、
②、
能不能把它们看成函数值?
新课引入
认真观察并回答下列问题:
(1)、一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
(2)、一根1米长的绳子从中间剪一次剩下 米,再从中间剪一次剩下 米,若这条绳子剪x次剩下y米,则y与x的函数关系是:
新课引入
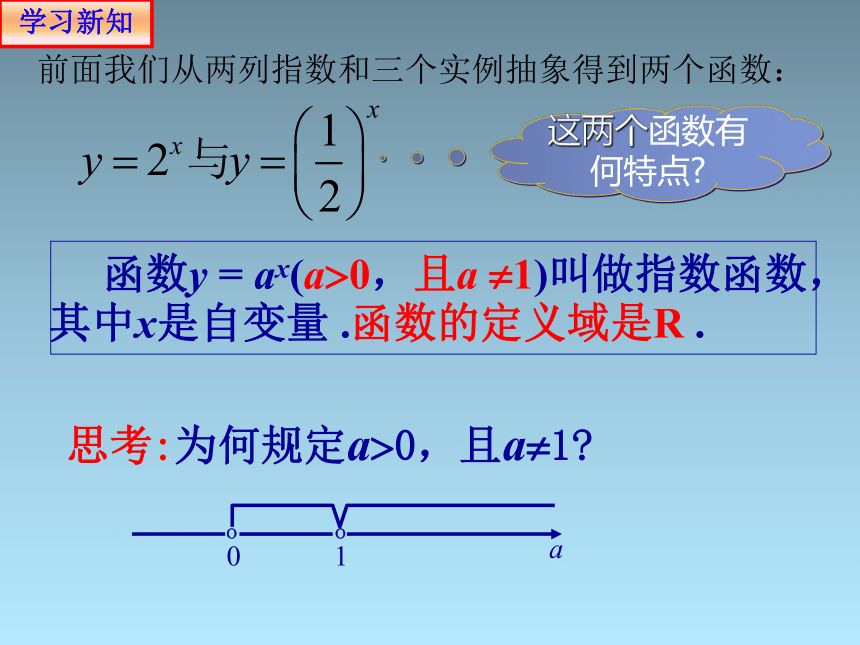
前面我们从两列指数和三个实例抽象得到两个函数:
这两个函数有何特点
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
思考:为何规定a 0,且a 1
0
1
a
学习新知
当a 0时,ax有些会没有意义,如(-2) , 0 等都没有意义;
0
1
a
而当a=1时,函数值y恒等于1,没有研究的必要.
思考:为何规定a 0,且a 1
▲关于指数函数的定义域:
回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,所以指数函数的定义域是R。
学习新知
学习新知
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
例1:下列函数中指数函数的个数是:
答案:1个
典型例题
判断一个函数是指数函数的方法
(1)需判断其解析式是否符合y=ax(a>0,且a≠1)这一结构特征.
(2)看是否具备指数函数解析式所具有的所有特征.只要有一个特征不具备,则该函数不是指数函数.
典型例题
典型例题
(1)求指数函数的解析式时,一般采用待定系数法,即先设出函数的解析式,然后利用已知条件,求出解析式中的参数,从而得到函数的解析式,其中掌握指数函数的概念是解决这类问题的关键.
(2)求指数函数的函数值的关键是掌握指数函数的解析式
方法总结
巩固练习
C
2
典型例题
典型例题
方法总结
巩固练习
A
A
巩固练习
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
课堂小结
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
4.2.1指数函数的概念
传说古印度的宰相西萨发明了国际象棋,国王很喜欢这个游戏,决定奖赏他,表示可以满足他任何一个要求。宰相微笑着说出了他的要求:在他的棋盘上摆满麦粒,第1格放1粒,第2格放2粒,第3格放4粒……每一小格的麦粒数量都是前一格的2倍,直至所有格子都摆满。国王马上派人搬来麦粒开始摆放,但很快他发现这个要求根本不可能满足,因为所有麦粒的总和是个天文数字。
到底需要多少粒小麦呢?这是一个20位数,一个天文数字。这个数字的小麦折算成重量,约为2587亿吨。即使现在,全世界小麦年产量也达不到这个数字。有人说,用80立方米的仓库存放这些小麦,把这些仓库连接起来,可以从地球一直延伸到太阳。
新课引入
新课引入
随看中国经济高速增长,人民生活水平不断提高,旅游成了越来越多家庭的重要生活方式,由于旅游人数不断增加,A,B两地景区自2001年起采取了不同的应对措施,A地提高了景区门票价格,而B地则取消了景区门票.右表给出了A,B两地景区2001年至2015年的游客人次以及逐年增加量。
比较两地景区游客人次的变化情况,你发现了怎样的变化规律?
新课引入
为了有利于观察规律,根据表格,分别画出A,B两地景区采取不同措施后的15年游客人次的图象
观察图象和表格,可以发现,A地景区的游客人次近似于直线上升(线性增长),年增加量大致相等(约为10万次);B地景区的游客人次则是非线性增长,年增加量越来越大,但从图象和年增加量都难以看出变化规律.
新课引入
结果表明,B地景区的游客人次的年增长率都约为
1.11-1=0.11,是一个常数。
像这样,增长率为常数的变化方式,我们称为指数增长.因此,B地景区的游客人次近似于指数增长.
显然,从2001年开始,B地景区游客人次的变化规律以近似描述为:
从2002年起,将B地景区每年的游客人次除以上一年的游客人次,可以得到
…………
1年后,游客人次是2001年的1.111倍;
2年后,游客人次是2001年的1.112倍;
3年后,游客人次是2001年的1.113倍;
...x年后,游客人次是2001年的1.11x倍。
如果设经过x年后的游客人次为2001年的y倍,
那么y=1.11x(x∈[0,+∞)这是一个函数,其中指数x是自变量。
细胞分裂过程
细胞个数
第一次
第二次
第三次
2=21
8=23
4=22
…………
第x次
……
细胞个数y关于分裂次数x的表达为
表达式
新课引入
比较下列指数的异同,
若是函数值?是什么函数?
①、
②、
能不能把它们看成函数值?
新课引入
认真观察并回答下列问题:
(1)、一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
(2)、一根1米长的绳子从中间剪一次剩下 米,再从中间剪一次剩下 米,若这条绳子剪x次剩下y米,则y与x的函数关系是:
新课引入
前面我们从两列指数和三个实例抽象得到两个函数:
这两个函数有何特点
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
思考:为何规定a 0,且a 1
0
1
a
学习新知
当a 0时,ax有些会没有意义,如(-2) , 0 等都没有意义;
0
1
a
而当a=1时,函数值y恒等于1,没有研究的必要.
思考:为何规定a 0,且a 1
▲关于指数函数的定义域:
回顾上一节的内容,我们发现指数 中p可以是有理数也可以是无理数,所以指数函数的定义域是R。
学习新知
学习新知
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
例1:下列函数中指数函数的个数是:
答案:1个
典型例题
判断一个函数是指数函数的方法
(1)需判断其解析式是否符合y=ax(a>0,且a≠1)这一结构特征.
(2)看是否具备指数函数解析式所具有的所有特征.只要有一个特征不具备,则该函数不是指数函数.
典型例题
典型例题
(1)求指数函数的解析式时,一般采用待定系数法,即先设出函数的解析式,然后利用已知条件,求出解析式中的参数,从而得到函数的解析式,其中掌握指数函数的概念是解决这类问题的关键.
(2)求指数函数的函数值的关键是掌握指数函数的解析式
方法总结
巩固练习
C
2
典型例题
典型例题
方法总结
巩固练习
A
A
巩固练习
函数y = ax(a 0,且a 1)叫做指数函数,其中x是自变量 .函数的定义域是R .
课堂小结
(1)定义域必须是实数集R;
(2)自变量是x,x位于指数位置上,且指数位置上只有x这一项;
(3)指数式只有一项,并且指数式的系数为1,例如y=5·ax(a>0且a≠1)不是指数函数;
(4)底数a的范围必须是a>0且a≠1.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
