人教版高中数学新教材必修第一册课件:4.5.3函数模型的应用实例(共34张PPT)
文档属性
| 名称 | 人教版高中数学新教材必修第一册课件:4.5.3函数模型的应用实例(共34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
4.5.2函数模型的应用实例
我们学过的基本初等函数有一次函数,二次函数,反比例函数,指数函数,对数函数以及幂函数.它们都与现实世界有着紧密的联系,有着广泛的应用.
下面我们通过一些实例,来感受它们的广泛应用,体会解决实际问题建立函数模型的过程.
1.一次函数的解析式为____________ , 其图像是一条____线,当_______时,一次函数在 上为增函数,当_____时,一次函数在 上为减函数。
直
2.二次函数的解析式为____________, 其图像是一条____线,当______时,
函数有最小值为_______,当__ _时,函数有最大值为________。
抛物
复习引入
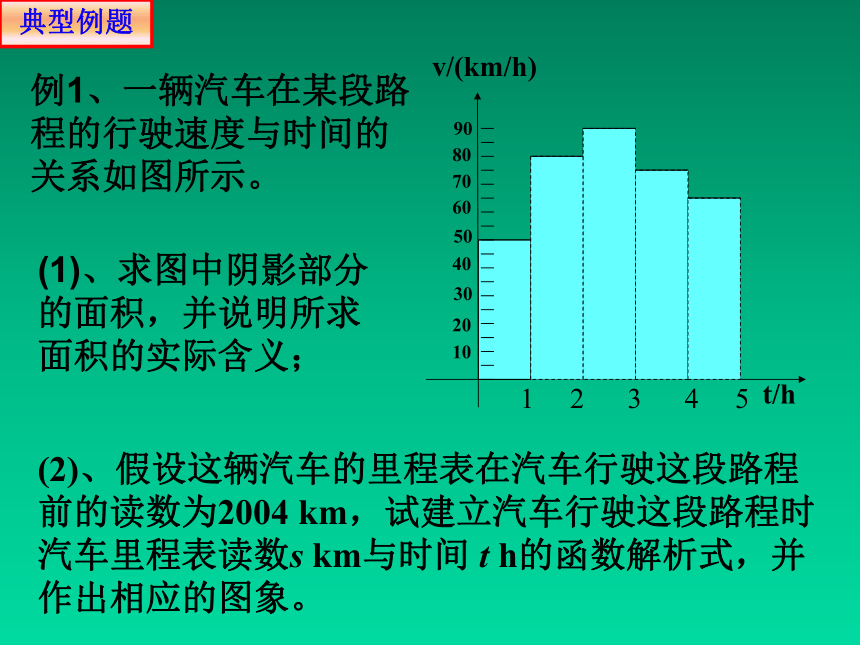
例1、一辆汽车在某段路程的行驶速度与时间的关系如图所示。
(1)、求图中阴影部分的面积,并说明所求面积的实际含义;
(2)、假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间 t h的函数解析式,并作出相应的图象。
90
80
70
60
50
40
30
20
10
v/(km/h)
t/h
1 2 3 4 5
典型例题
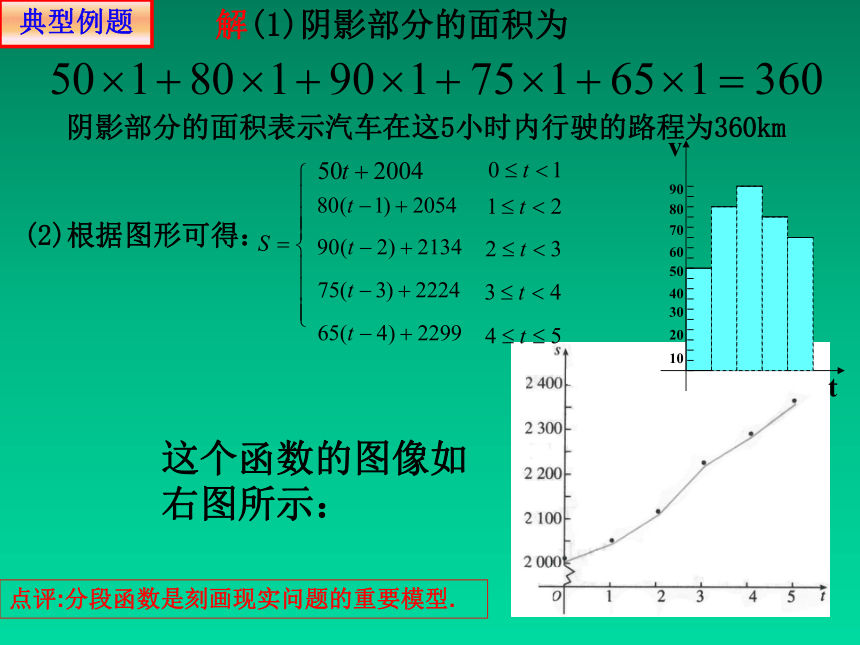
这个函数的图像如右图所示:
解(1)阴影部分的面积为
阴影部分的面积表示汽车在这5小时内行驶的路程为360km
(2)根据图形可得:
点评:分段函数是刻画现实问题的重要模型.
90
80
70
60
50
40
30
20
10
v
t
典型例题
1.下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事。
①小明离开家不久,发现自己把作业忘在家里,于是返回家里找到作业再上学
②小明骑车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间
③小明出发后,心情轻松,缓慢行进,后来为了赶时间开始加速
(D)
(A)
(B)
c对应的参考事件:小明出发后感到时间较紧,所以加速前进,后来发现时间还很充裕,于是放慢了速度。
A
B
C
0
离家
距离
时间
0
时间
0
时间
0
时间
D
离家
距离
离家
距离
离家
距离
巩固练习
2.在一定范围内,某种产品的购买量为y t,与单价X元之间满足一次函数关系如果购买1000t,每吨为800元,如果购买2000t,每吨为700元,一客户购买400t,单价应该为( )
A.820元 B.840元
C.860元 D.880元
c
巩固练习
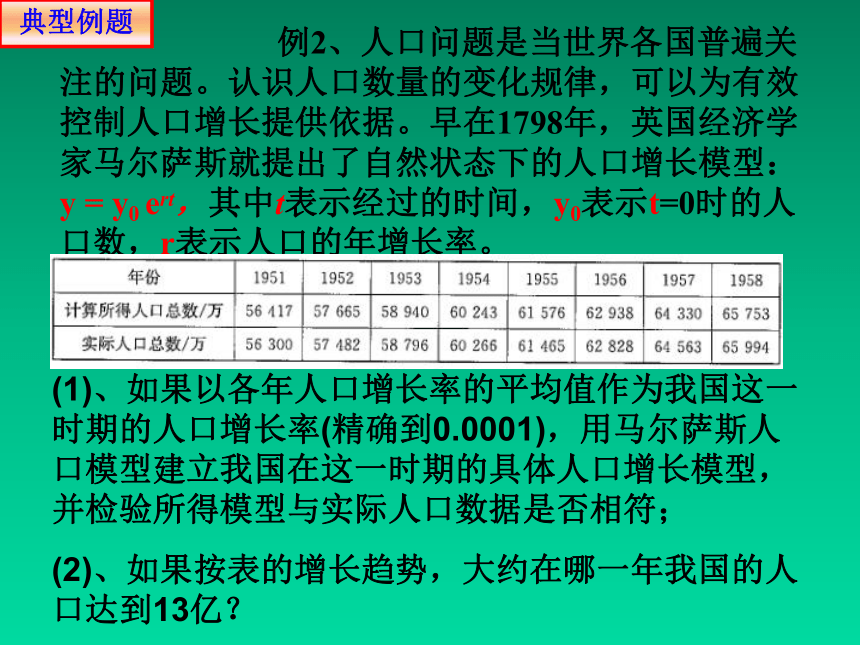
例2、人口问题是当世界各国普遍关注的问题。认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:y = y0 ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年增长率。
(1)、如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)、如果按表的增长趋势,大约在哪一年我国的人口达到13亿?
典型例题
典型例题
典型例题
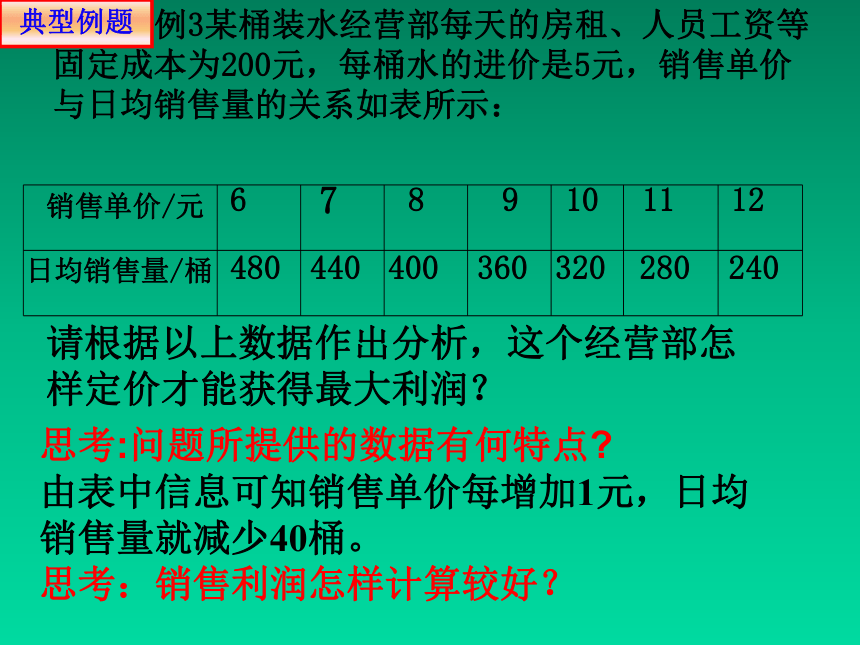
例3某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
销售单价/元
日均销售量/桶
6
7
8
9
10
11
12
480
440
400
360
320
280
240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
由表中信息可知销售单价每增加1元,日均销售量就减少40桶。
思考:销售利润怎样计算较好?
思考:问题所提供的数据有何特点
典型例题
例3:某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:
销售单价(元) 6 7 8 9 10 11 12
日均销售量(桶) 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润
解:由表可知:销售单价每增加1元,日均销售量就减少40桶.
设在进价基础上增加x元,日均销售利润为y元,
而在此情况下的日均销售量就为:480-40(x-1)=520-40x(桶).
∵x>0,且520-40x>0 ∴0从而y=(520-40x)x-200=-40x2+520x-200, 0∴当x=6.5时,y有最大值.
∴经营部只要将销售单价定为11.5元,就能获得最大利润.
注意变量的变化范围,并以此检验结果的合理性.
典型例题
互动交流,探求新知
例4、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
回报的累积值
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
请问,你会选择哪种投资方案呢?
1.考虑回报量,除了要考虑每天的回报量之外,还得考虑什么
想一想:
方案一:每天回报40元;
我来说
①例4涉及哪些数量关系?
②如何用函数描述这些数量关系?
思考下面的问题:
投资天数
回报金额
③三个函数模型的增减性如何?
④要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
每天的回报数、增加量、累计回报数
想一想:
2.本题中涉及哪些数量关系 如何利用函数描述这些数量关系
我来说
设第x天所得回报是y元,则方案一可用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数
进行描述。
想一想:
3.怎样去研究这三个函数,才能找到最佳的方案呢
要对三个方案作出选择,就要对它们的增长情况进行分析,用计算器计算出三种方案所得回报的增长情况,列表如下:
我来说
x/天 方案一 方案二 方案三
y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
… … … …
30 40 300 214748364.8
0
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
我想问
根据所列的表格中提供的数据,你对三种方案分别表现出的回报资金的增长差异有什么认识
我来说
方案一每天的回报不变;方案二、三每天的回报都在增加,且方案三随x的增加每天的回报越来越大,比方案二要大得多。
我想问
作出三个方案的图象看看
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
根据以上分析,你认为该作出何种选择
从问题1可知,考虑回报量,除了要考虑每天的回报量之外,还得考虑回报的累积值.你能把前11天回报的累积值算出来吗
累计回报表
天数
方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
思考
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
基本步骤:
第一步:阅读理解,认真审题
读懂题中的文字叙述,理解叙述所反映的实际背景,领悟从背景中概括出来的数学实质,尤其是理解叙述中的新名词、新概念,进而把握住新信息。
第二步:引进数学符号,建立数学模型
设自变量为x,函数为y,并用x表示各相关量,然后根据问题已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为一个数学问题,实现问题的数学化,即所谓建立数学模型。
第三步:利用数学的方法将得到的常规数学问题(即数学模型)予以解答,求得结果。
第四步:再转译为具体问题作出解答。
方法归纳
实际问题
数学模型
实际问题 的解
抽象概括
数学模型 的解
还原说明
推理
演算
方法归纳
1.一家旅社有100间相同的客房,经过一段时间的经营实践,旅社经理发现,每间客房每天的价格与住房率之间有如下关系:
每间每天房价
住房率
20元
18元
16元
14元
65%
75%
85%
95%
要使每天收入达到最高,每间定价应为( )
A.20元 B.18元 C.16元 D.14元
2.将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少20个,为了取得最大利润,每个售价应定为( )
A.95元 B.100元 C.105元 D.110元
C
A
巩固练习
收集数据
画散点图
选择函数模型
求函数模型
检验
用函数模型解释问题
不符合实际
小结:函数建模
实际情境
提出问题
数学模型
数学结果
检验
可用结果
合乎实际
不合乎实际
收集数据
画散点图
选择数学模型
求函数模型
检验
用函数模型解释实际问题
符合实际
不符合实际
一次函数
对数函数
指数函数
①例6涉及了哪几类函数模型?
用3分钟时间认真阅读课本152页例6,边阅读边思考下面的问题:
②你能用数学语言描述符合公司奖励方案的条件吗
[例6] 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?
1、销售利润达到10万元时进行奖励;
2、奖金总数不超过5万元;
3、奖金不超过利润的25%;
4、公司总的利润目标为1000万元。
从1和4知道只需在区间[10,1000]上检
验三个模型是否符合公司的要求(即2
和3两条)即可。
3.依据这个模型进行奖励时,奖金不超过利润的25%,
所以奖金y可用不等式表示为______________.
2.依据这个模型进行奖励时,奖金总数不超过5万元,
所以奖金y可用不等式表示为__________.
0≤y≤5
0≤y≤25%x
依据这两个约束条件对奖励模型进行选择的实质是要怎么样呢?
比较三个函数的增长情况!
尝试作函数:
y=0.25x, y=log7x+1,
y=1.002x,及y=5的图象.并思考:
不妨试一试!
1.如何利用它们的图象作出选择呢?
2.这三种增长有什么不同呢?
▲ 借助计算机作出它们的图象。通过观察图象,你认为哪个模型符合公司的奖励方案?
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;
②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;
③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求。
对数增长模型比较适合于描述增长速度平缓的变化规律
是否满足条件3,即 “奖金不超过利润的25%”呢?
y
x
1
2
3
4
5
6
7
8
0
f(x)=log7x+1-0.25x
1
-1
根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.
f(x)=log7x+1-0.25x
这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.
所以,模型 确实能符合公司的要求。
练一练
探究:你能否仿照前面例题使用的方法,探索研究幂函数 .
指数函数 .
对数函数
在区间(0,+∞)上的增长差异
2.(选做)甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,
提供了两个方面的信息,如下图:
甲调查表明:每个甲鱼池平均产量从第1年1万只甲鱼上升到第6年2万只
乙调查表明:甲鱼池个数由第1年30个减少到第6年10个
请你根据提供的信息说明:
①第2年甲鱼池的个数及全县甲鱼总数
②到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由。
布置作业
1 . (必做)课本第156页 第11题
4.5.2函数模型的应用实例
我们学过的基本初等函数有一次函数,二次函数,反比例函数,指数函数,对数函数以及幂函数.它们都与现实世界有着紧密的联系,有着广泛的应用.
下面我们通过一些实例,来感受它们的广泛应用,体会解决实际问题建立函数模型的过程.
1.一次函数的解析式为____________ , 其图像是一条____线,当_______时,一次函数在 上为增函数,当_____时,一次函数在 上为减函数。
直
2.二次函数的解析式为____________, 其图像是一条____线,当______时,
函数有最小值为_______,当__ _时,函数有最大值为________。
抛物
复习引入
例1、一辆汽车在某段路程的行驶速度与时间的关系如图所示。
(1)、求图中阴影部分的面积,并说明所求面积的实际含义;
(2)、假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间 t h的函数解析式,并作出相应的图象。
90
80
70
60
50
40
30
20
10
v/(km/h)
t/h
1 2 3 4 5
典型例题
这个函数的图像如右图所示:
解(1)阴影部分的面积为
阴影部分的面积表示汽车在这5小时内行驶的路程为360km
(2)根据图形可得:
点评:分段函数是刻画现实问题的重要模型.
90
80
70
60
50
40
30
20
10
v
t
典型例题
1.下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事。
①小明离开家不久,发现自己把作业忘在家里,于是返回家里找到作业再上学
②小明骑车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间
③小明出发后,心情轻松,缓慢行进,后来为了赶时间开始加速
(D)
(A)
(B)
c对应的参考事件:小明出发后感到时间较紧,所以加速前进,后来发现时间还很充裕,于是放慢了速度。
A
B
C
0
离家
距离
时间
0
时间
0
时间
0
时间
D
离家
距离
离家
距离
离家
距离
巩固练习
2.在一定范围内,某种产品的购买量为y t,与单价X元之间满足一次函数关系如果购买1000t,每吨为800元,如果购买2000t,每吨为700元,一客户购买400t,单价应该为( )
A.820元 B.840元
C.860元 D.880元
c
巩固练习
例2、人口问题是当世界各国普遍关注的问题。认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:y = y0 ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年增长率。
(1)、如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)、如果按表的增长趋势,大约在哪一年我国的人口达到13亿?
典型例题
典型例题
典型例题
例3某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
销售单价/元
日均销售量/桶
6
7
8
9
10
11
12
480
440
400
360
320
280
240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
由表中信息可知销售单价每增加1元,日均销售量就减少40桶。
思考:销售利润怎样计算较好?
思考:问题所提供的数据有何特点
典型例题
例3:某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:
销售单价(元) 6 7 8 9 10 11 12
日均销售量(桶) 480 440 400 360 320 280 240
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润
解:由表可知:销售单价每增加1元,日均销售量就减少40桶.
设在进价基础上增加x元,日均销售利润为y元,
而在此情况下的日均销售量就为:480-40(x-1)=520-40x(桶).
∵x>0,且520-40x>0 ∴0
∴经营部只要将销售单价定为11.5元,就能获得最大利润.
注意变量的变化范围,并以此检验结果的合理性.
典型例题
互动交流,探求新知
例4、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
回报的累积值
方案二:第一天回报10元,以后每天比前一天多 回报10元;
方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。
请问,你会选择哪种投资方案呢?
1.考虑回报量,除了要考虑每天的回报量之外,还得考虑什么
想一想:
方案一:每天回报40元;
我来说
①例4涉及哪些数量关系?
②如何用函数描述这些数量关系?
思考下面的问题:
投资天数
回报金额
③三个函数模型的增减性如何?
④要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
每天的回报数、增加量、累计回报数
想一想:
2.本题中涉及哪些数量关系 如何利用函数描述这些数量关系
我来说
设第x天所得回报是y元,则方案一可用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数
进行描述。
想一想:
3.怎样去研究这三个函数,才能找到最佳的方案呢
要对三个方案作出选择,就要对它们的增长情况进行分析,用计算器计算出三种方案所得回报的增长情况,列表如下:
我来说
x/天 方案一 方案二 方案三
y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
… … … …
30 40 300 214748364.8
0
0
0
0
0
0
0
0
0
…
0
10
10
10
10
10
10
10
10
…
10
0.4
0.8
1.6
3.2
6.4
12.8
25.6
51.2
…
107374182.4
我想问
根据所列的表格中提供的数据,你对三种方案分别表现出的回报资金的增长差异有什么认识
我来说
方案一每天的回报不变;方案二、三每天的回报都在增加,且方案三随x的增加每天的回报越来越大,比方案二要大得多。
我想问
作出三个方案的图象看看
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。
根据以上分析,你认为该作出何种选择
从问题1可知,考虑回报量,除了要考虑每天的回报量之外,还得考虑回报的累积值.你能把前11天回报的累积值算出来吗
累计回报表
天数
方案 1 2 3 4 5 6 7 8 9 10 11
一 40 80 120 160 200 240 280 320 360 400 440
二 10 30 60 100 150 210 280 360 450 550 660
三 0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 816.8
思考
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
基本步骤:
第一步:阅读理解,认真审题
读懂题中的文字叙述,理解叙述所反映的实际背景,领悟从背景中概括出来的数学实质,尤其是理解叙述中的新名词、新概念,进而把握住新信息。
第二步:引进数学符号,建立数学模型
设自变量为x,函数为y,并用x表示各相关量,然后根据问题已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系式,将实际问题转化为一个数学问题,实现问题的数学化,即所谓建立数学模型。
第三步:利用数学的方法将得到的常规数学问题(即数学模型)予以解答,求得结果。
第四步:再转译为具体问题作出解答。
方法归纳
实际问题
数学模型
实际问题 的解
抽象概括
数学模型 的解
还原说明
推理
演算
方法归纳
1.一家旅社有100间相同的客房,经过一段时间的经营实践,旅社经理发现,每间客房每天的价格与住房率之间有如下关系:
每间每天房价
住房率
20元
18元
16元
14元
65%
75%
85%
95%
要使每天收入达到最高,每间定价应为( )
A.20元 B.18元 C.16元 D.14元
2.将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少20个,为了取得最大利润,每个售价应定为( )
A.95元 B.100元 C.105元 D.110元
C
A
巩固练习
收集数据
画散点图
选择函数模型
求函数模型
检验
用函数模型解释问题
不符合实际
小结:函数建模
实际情境
提出问题
数学模型
数学结果
检验
可用结果
合乎实际
不合乎实际
收集数据
画散点图
选择数学模型
求函数模型
检验
用函数模型解释实际问题
符合实际
不符合实际
一次函数
对数函数
指数函数
①例6涉及了哪几类函数模型?
用3分钟时间认真阅读课本152页例6,边阅读边思考下面的问题:
②你能用数学语言描述符合公司奖励方案的条件吗
[例6] 某公司为了实现1000万元利润的目标,准备制定
一个激励销售人员的奖励方案:在销售利润达到10万
元时,按销售利润进行奖励,且奖金y (单位:万元)
随销售利润x(单位:万元)的增加而增加,但奖金
总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,
其中哪个模型能符合公司的要求?
1、销售利润达到10万元时进行奖励;
2、奖金总数不超过5万元;
3、奖金不超过利润的25%;
4、公司总的利润目标为1000万元。
从1和4知道只需在区间[10,1000]上检
验三个模型是否符合公司的要求(即2
和3两条)即可。
3.依据这个模型进行奖励时,奖金不超过利润的25%,
所以奖金y可用不等式表示为______________.
2.依据这个模型进行奖励时,奖金总数不超过5万元,
所以奖金y可用不等式表示为__________.
0≤y≤5
0≤y≤25%x
依据这两个约束条件对奖励模型进行选择的实质是要怎么样呢?
比较三个函数的增长情况!
尝试作函数:
y=0.25x, y=log7x+1,
y=1.002x,及y=5的图象.并思考:
不妨试一试!
1.如何利用它们的图象作出选择呢?
2.这三种增长有什么不同呢?
▲ 借助计算机作出它们的图象。通过观察图象,你认为哪个模型符合公司的奖励方案?
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
①对于模型y=0.25x,它在区间[10,1000]上递增,
当x>20时,y>5,因此该模型不符合要求;
②对于模型y=1.002x,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x>806时,y>5,因此
该模型不符合要求;
③对于模型y=log7x+1,它在区间[10,1000]上递增,
观察图象并结合计算可知,当x=1000时,
y=log71000+1≈4.55<5,所以它符合奖金总数不超过
5万元的要求。
对数增长模型比较适合于描述增长速度平缓的变化规律
是否满足条件3,即 “奖金不超过利润的25%”呢?
y
x
1
2
3
4
5
6
7
8
0
f(x)=log7x+1-0.25x
1
-1
根据图象观察,f(x)=log7x+1-0.25x的图象在区间[10,1000]内的确在x轴的下方.
f(x)=log7x+1-0.25x
这说明,按模型y=log7x+1奖励,奖金不会超过利润的25%.
所以,模型 确实能符合公司的要求。
练一练
探究:你能否仿照前面例题使用的方法,探索研究幂函数 .
指数函数 .
对数函数
在区间(0,+∞)上的增长差异
2.(选做)甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,
提供了两个方面的信息,如下图:
甲调查表明:每个甲鱼池平均产量从第1年1万只甲鱼上升到第6年2万只
乙调查表明:甲鱼池个数由第1年30个减少到第6年10个
请你根据提供的信息说明:
①第2年甲鱼池的个数及全县甲鱼总数
②到第6年这个县的甲鱼养殖业的规模比第1年是扩大了还是缩小了?说明理由。
布置作业
1 . (必做)课本第156页 第11题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
