黑龙江省鸡西市晨兴中学2021-2022学年八年级下学期期中考试数学试题(图片版含答案)
文档属性
| 名称 | 黑龙江省鸡西市晨兴中学2021-2022学年八年级下学期期中考试数学试题(图片版含答案) |
|
|
| 格式 | |||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-12 15:57:41 | ||
图片预览



文档简介
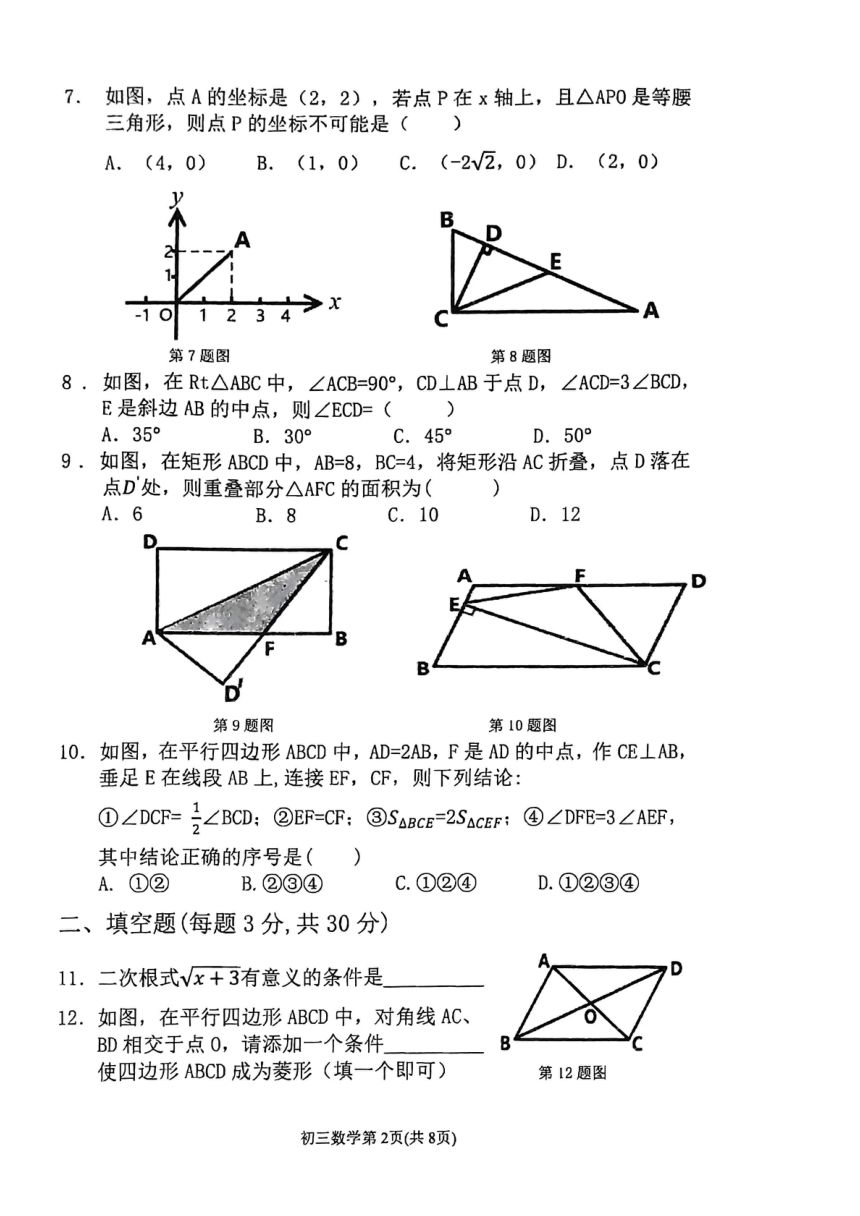
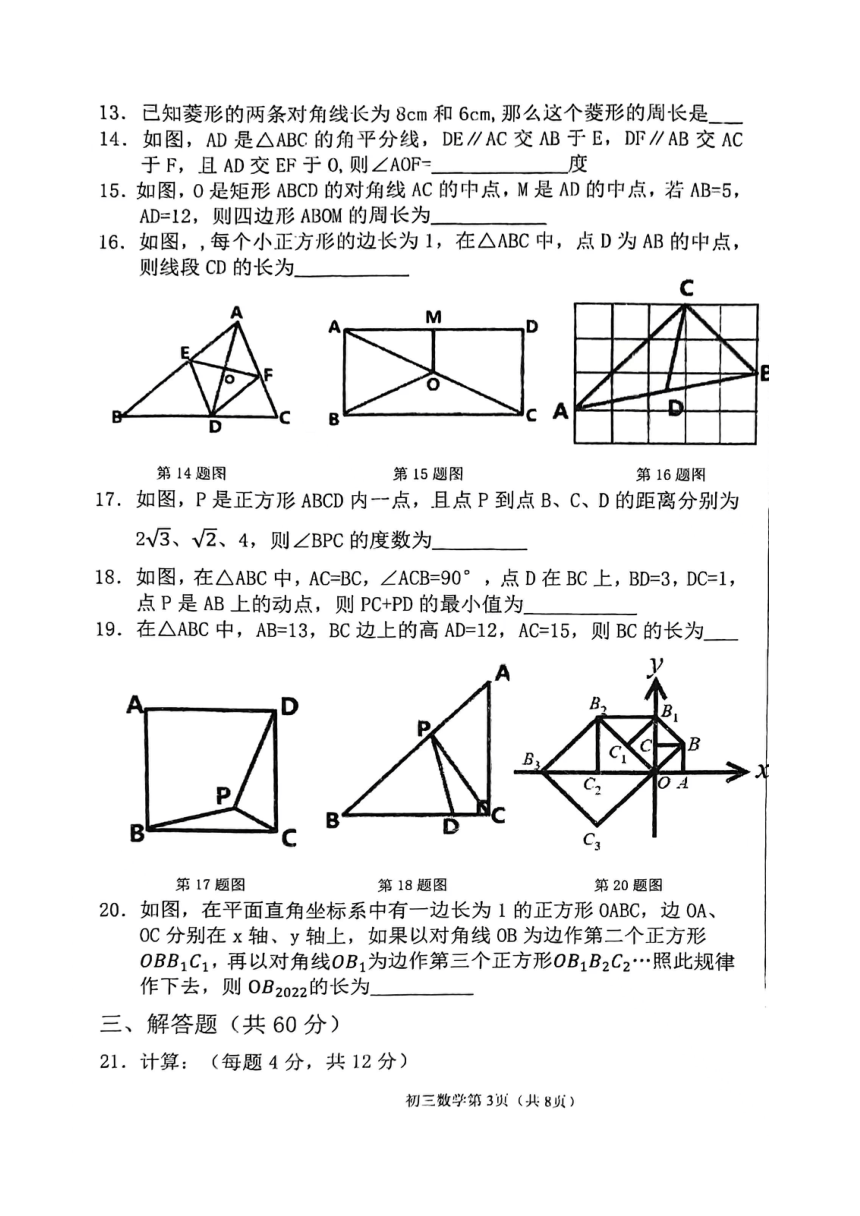
2021-2022 鸡西市第二学期八年级数学期中考试试题
1
2
3
4
5
6
7
8
试题答案
一、选择题(每题 3 分,共 30 分)
1、D 2、A 3、B 4、D 5、C
6、A 7、B 8、C 9、C 10、C
二、填空题(每题3 分,共 30 分)
11) x 3 12)AB=BC 等 13)20cm 14)90 15)20
26 2023
16) 17)135° 18)5 19)4 或14 20) 2
2
三、解答题(共 60 分)
21、计算:(每题 3 分,共 9 分)
① 8 + 2 3—( 27 2)
2 2 2 3 3 3 2 ……………………………………………………2 分
3 2 3 ……………………………………………………1 分
② (3 2+2 3()3 2 2 3)
(3 2)2 (2 3)2 ………………………………………………………1 分
18 12 ………………………………………………………1分
6 ………………………………………………………1分
2022 2022
③ (4 3 + 7) × (4 3—7)
2022 ....................................................................................................................... (4 3 7)(4 3 7) 1分
(48 49)2022 ………………………………………………………1 分
( 1)2022
1 ………………………………………………………1 分
9
22、化简求值:(本题满分6 分)
x (x 1)
2 x2 1
解:原式= x 2 x 2 x 1
x (x 1)
2
x 1
= x 2 x 2 (x 1)(x 1)................................................................1分
x x
= x 2 1 ………………………………………………………1 分
x 2
1 1
= x 2 或 x 2 ………………………………………………………2 分
1 3.................................................
当 x 3 2 时,原式= 2分
3 2 2 3
23.解:
在 Rt△ACD 中,AD=4,CD=3
∴AC = AD2 + CD2=5..............................................................2分
在△ABC 中,
∵AC2 + BC2=52 + 122=132=AB2........................................................... 1分
∴△ABC为直角三角形;............................................................... 2分
∴图形面积为:
1 1
S△ABC-S△ACD= ×5×12- ×3×4=24...................................2分
2 2
24.∵a2+ b2+c2+338-10a-24b-26c=0
2 2 2
∴ (a 5) + (b 12) + (c 13) =0..................2分
2 2 2
(a 5) ≥0,(b 12) ≥0,(c 13) ≥0.....................1 分
∴a=5, b=12, c=13..................................................................2 分
10
又∵52+ 122=132
∴△ABC为直角三角形................................................................... 2分
25.
证明:(方法不唯一,成立即可)
如图,取 BF的中点 G,连接 DG.................................................2分
∵AD 是△ABC 的中线,
∴D 为 BC 边的中点
∴DG是△BCF的中位线..................................................................2分
1
∴DG= CF,DG∥CF
2
∴∠1=∠2,∠3=∠4
又 E 为 AD 的中点,
∴AE=DE
∴△AEF≌△DEG............................................................................ 3分
∴AF=DG 1∴AF= CF........................................................................... 1分
2
26.
证明:(1)DE∥AC,DF∥AB,
∴四边形DEAF为平行四边形(两组对边分别平行的四边形是平行
四边形).......................................................................................... 2分
∴DE=AF,DF=AE(平行四边形对边分别相等)..............................1分
又∵AB=AC
∴∠B=∠C......................................................................................1分
∴∠EDB=∠B
∴ DE=BE.....................................................................................1分
11
∴ DE+DF=AB=AC........................................................................1 分
(2)图(2)中猜想:AC+DF=DE,......................................................1分
图(3)中猜想:AC+DE=DF..............................................................1分
27.解(1)|OA-2|+(OC 4)2=0
∴OA-2=0,OC 4=0
∴OA=2,OC=4................................................................................. 2分
∵四边形 OABC 是矩形
∴BC=OA=2, BA=OC=4
C点的坐标为(4,0),点 B的坐标为(4,2)..........................2分
(2) 四边形 OABC 是矩形,
∴BC=OA,∠AOD=∠B=90°
由折叠可知,∠B=∠B'=90°,BC=B'C
∴OA=B'C, ∠AOD=∠B'=90°
∵∠ADO=∠CDB'
∴△ADO≌△CDB'..........................................................................2 分
∴AD=CD
设 AD=CD=x,则 OD=4-x,
在 Rt△AOD 中,
∵AD2= OA2+ OD2
∴22+ (4 X)2= X2
5
解得 x= ………………………………………1 分
2
12
5 11 5
(3)存在由 P的坐标为(- ,2)或( ,-2)或( ,2) ……(3分)
2 2 2
13
1
2
3
4
5
6
7
8
试题答案
一、选择题(每题 3 分,共 30 分)
1、D 2、A 3、B 4、D 5、C
6、A 7、B 8、C 9、C 10、C
二、填空题(每题3 分,共 30 分)
11) x 3 12)AB=BC 等 13)20cm 14)90 15)20
26 2023
16) 17)135° 18)5 19)4 或14 20) 2
2
三、解答题(共 60 分)
21、计算:(每题 3 分,共 9 分)
① 8 + 2 3—( 27 2)
2 2 2 3 3 3 2 ……………………………………………………2 分
3 2 3 ……………………………………………………1 分
② (3 2+2 3()3 2 2 3)
(3 2)2 (2 3)2 ………………………………………………………1 分
18 12 ………………………………………………………1分
6 ………………………………………………………1分
2022 2022
③ (4 3 + 7) × (4 3—7)
2022 ....................................................................................................................... (4 3 7)(4 3 7) 1分
(48 49)2022 ………………………………………………………1 分
( 1)2022
1 ………………………………………………………1 分
9
22、化简求值:(本题满分6 分)
x (x 1)
2 x2 1
解:原式= x 2 x 2 x 1
x (x 1)
2
x 1
= x 2 x 2 (x 1)(x 1)................................................................1分
x x
= x 2 1 ………………………………………………………1 分
x 2
1 1
= x 2 或 x 2 ………………………………………………………2 分
1 3.................................................
当 x 3 2 时,原式= 2分
3 2 2 3
23.解:
在 Rt△ACD 中,AD=4,CD=3
∴AC = AD2 + CD2=5..............................................................2分
在△ABC 中,
∵AC2 + BC2=52 + 122=132=AB2........................................................... 1分
∴△ABC为直角三角形;............................................................... 2分
∴图形面积为:
1 1
S△ABC-S△ACD= ×5×12- ×3×4=24...................................2分
2 2
24.∵a2+ b2+c2+338-10a-24b-26c=0
2 2 2
∴ (a 5) + (b 12) + (c 13) =0..................2分
2 2 2
(a 5) ≥0,(b 12) ≥0,(c 13) ≥0.....................1 分
∴a=5, b=12, c=13..................................................................2 分
10
又∵52+ 122=132
∴△ABC为直角三角形................................................................... 2分
25.
证明:(方法不唯一,成立即可)
如图,取 BF的中点 G,连接 DG.................................................2分
∵AD 是△ABC 的中线,
∴D 为 BC 边的中点
∴DG是△BCF的中位线..................................................................2分
1
∴DG= CF,DG∥CF
2
∴∠1=∠2,∠3=∠4
又 E 为 AD 的中点,
∴AE=DE
∴△AEF≌△DEG............................................................................ 3分
∴AF=DG 1∴AF= CF........................................................................... 1分
2
26.
证明:(1)DE∥AC,DF∥AB,
∴四边形DEAF为平行四边形(两组对边分别平行的四边形是平行
四边形).......................................................................................... 2分
∴DE=AF,DF=AE(平行四边形对边分别相等)..............................1分
又∵AB=AC
∴∠B=∠C......................................................................................1分
∴∠EDB=∠B
∴ DE=BE.....................................................................................1分
11
∴ DE+DF=AB=AC........................................................................1 分
(2)图(2)中猜想:AC+DF=DE,......................................................1分
图(3)中猜想:AC+DE=DF..............................................................1分
27.解(1)|OA-2|+(OC 4)2=0
∴OA-2=0,OC 4=0
∴OA=2,OC=4................................................................................. 2分
∵四边形 OABC 是矩形
∴BC=OA=2, BA=OC=4
C点的坐标为(4,0),点 B的坐标为(4,2)..........................2分
(2) 四边形 OABC 是矩形,
∴BC=OA,∠AOD=∠B=90°
由折叠可知,∠B=∠B'=90°,BC=B'C
∴OA=B'C, ∠AOD=∠B'=90°
∵∠ADO=∠CDB'
∴△ADO≌△CDB'..........................................................................2 分
∴AD=CD
设 AD=CD=x,则 OD=4-x,
在 Rt△AOD 中,
∵AD2= OA2+ OD2
∴22+ (4 X)2= X2
5
解得 x= ………………………………………1 分
2
12
5 11 5
(3)存在由 P的坐标为(- ,2)或( ,-2)或( ,2) ……(3分)
2 2 2
13
同课章节目录
