6.1.4数乘向量 课件(共15张PPT)
文档属性
| 名称 | 6.1.4数乘向量 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 09:18:02 | ||
图片预览



文档简介
(共15张PPT)
数乘向量
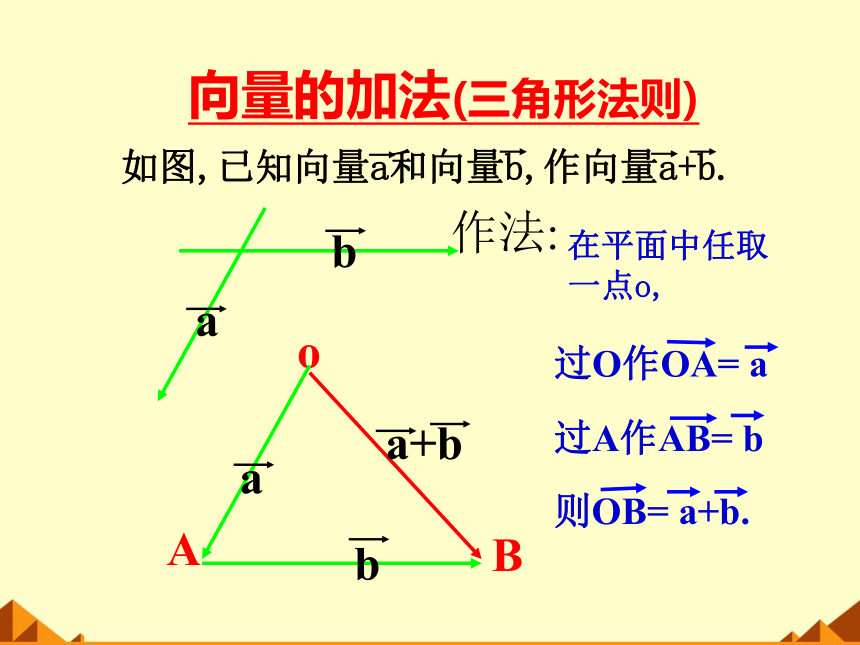
向量的加法(三角形法则)
a
b
作法:
在平面中任取
一点o,
o
过A作AB= b
过O作OA= a
则OB= a+b.
如图,已知向量a和向量b,作向量a+b.
a
A
b
B
a+b
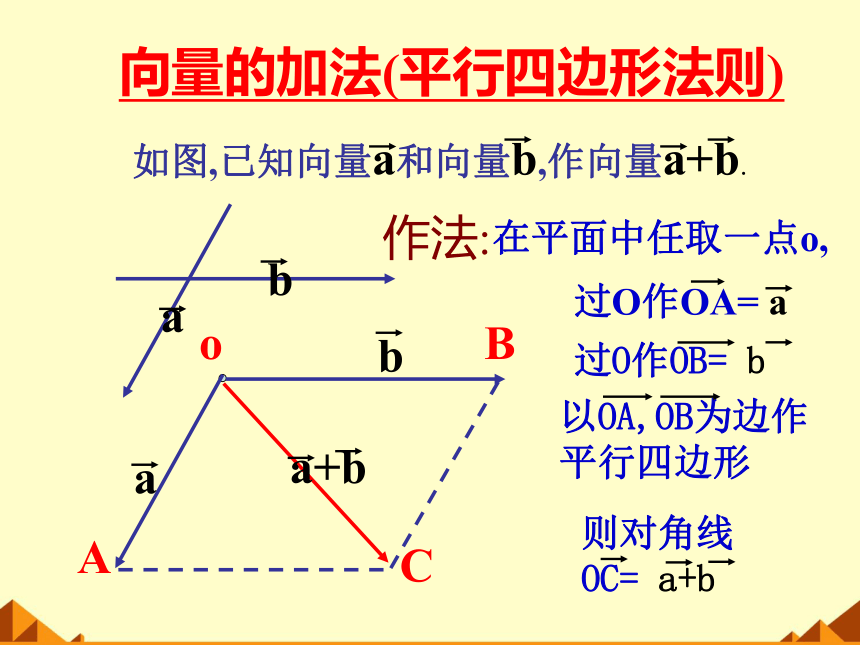
向量的加法(平行四边形法则)
a
作法:
在平面中任取一点o,
o
b
C
A
a
a+b
B
b
如图,已知向量a和向量b,作向量a+b.
过O作OA= a
过O作OB= b
以OA,OB为边作
平行四边形
则对角线
OC= a+b
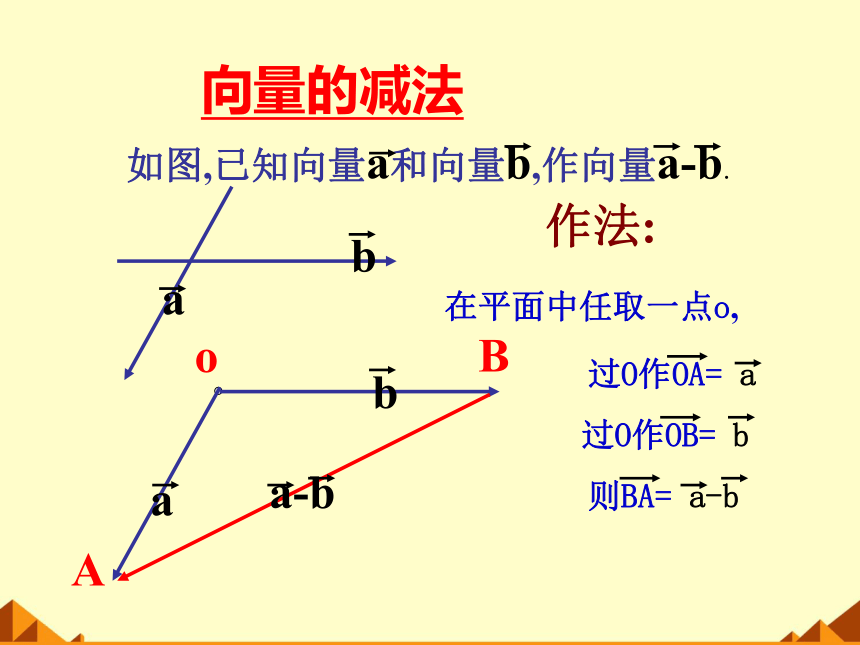
向量的减法
a
作法:
在平面中任取一点o,
o
过O作OB= b
过O作OA= a
则BA= a-b
b
b
B
a
A
a-b
如图,已知向量a和向量b,作向量a-b.
一只兔每次位移向量 ,
3次位移多少
次位移多少
a
3a
na
位移与速度的关系:
tv
s=
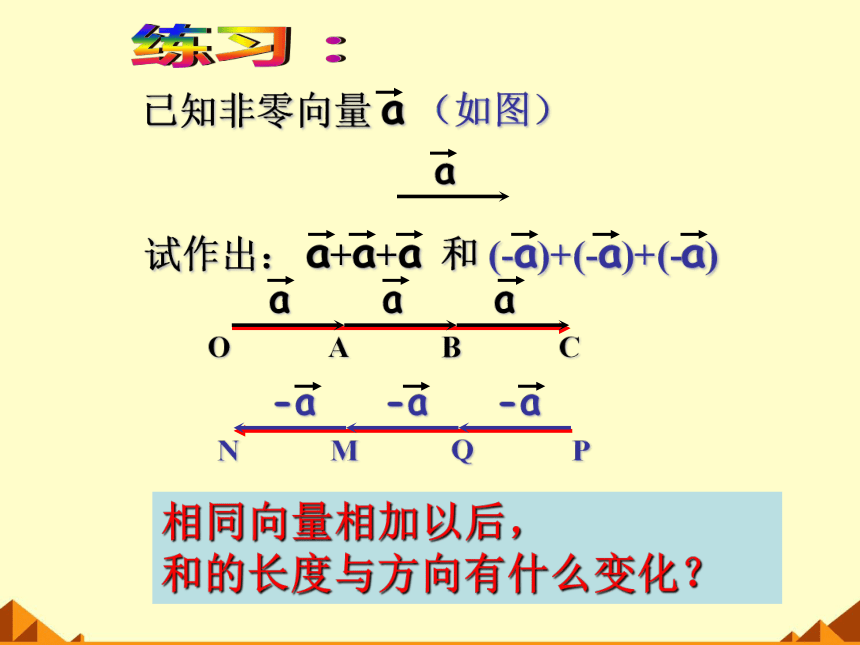
相同向量相加以后,
和的长度与方向有什么变化?
试作出: a+a+a 和 (-a)+(-a)+(-a)
练习:
已知非零向量 a (如图)
a
-a
-a
-a
P
Q
M
N
a
a
a
O
A
B
C
定义:
一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。
(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。
a
3(2a)=6a
3(2a)
2a
2b
2a+2b
b
a
a+b
2a+2b
2(a +
b)=
运算律:
设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
特别地:
-λa=-(λa) =λ(-a)
λ(a-b)=λa-λb
向量的加法、减法、数乘向量的综合运算叫向量的线性运算
练习1:若3m+2n=a,m-3n=b,其中a,b
是已知向量,求m,n.
-12a
5b
-a+5b-2c
例1 . 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)
(4) (λ+μ)(a-b)-(λ-μ)(a+b)
2μa-2λb
例2.设x是未知向量,解方程
5(x+a)+3(x-b)=0
例3:已知向量
试说明
,
,
的关系。
A
B
C
D
E
A
B
D
E
C
解:
∴ 与 共线且同向.
AE
A
B
D
C
练习2.在⊿ABC中,设D为BC的中点,求证:
求证:AD= (AB+AC)
1
2
A
B
C
O
a b
,
a
b
OB=a+2b,OC=a+3b
练习3. 已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
、
OA=a+b
a
b
2
b
3
b
数乘向量
向量的加法(三角形法则)
a
b
作法:
在平面中任取
一点o,
o
过A作AB= b
过O作OA= a
则OB= a+b.
如图,已知向量a和向量b,作向量a+b.
a
A
b
B
a+b
向量的加法(平行四边形法则)
a
作法:
在平面中任取一点o,
o
b
C
A
a
a+b
B
b
如图,已知向量a和向量b,作向量a+b.
过O作OA= a
过O作OB= b
以OA,OB为边作
平行四边形
则对角线
OC= a+b
向量的减法
a
作法:
在平面中任取一点o,
o
过O作OB= b
过O作OA= a
则BA= a-b
b
b
B
a
A
a-b
如图,已知向量a和向量b,作向量a-b.
一只兔每次位移向量 ,
3次位移多少
次位移多少
a
3a
na
位移与速度的关系:
tv
s=
相同向量相加以后,
和的长度与方向有什么变化?
试作出: a+a+a 和 (-a)+(-a)+(-a)
练习:
已知非零向量 a (如图)
a
-a
-a
-a
P
Q
M
N
a
a
a
O
A
B
C
定义:
一般地,实数λ与向量a的积是一个向量,
这种运算叫做向量的数乘运算,记作λa,
它的长度和方向规定如下:
(1) |λa|=|λ| |a|
(2) 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
特别地,当λ=0或a=0时, λa=0
(1) 根据定义,求作向量3(2a)和(6a) (a为非零向量),并进行比较。
(2) 已知向量 a,b,求作向量2(a+b)和2a+2b,并进行比较。
a
3(2a)=6a
3(2a)
2a
2b
2a+2b
b
a
a+b
2a+2b
2(a +
b)=
运算律:
设a,b为任意向量,λ,μ为任意实数,则有:
①λ(μa)=(λμ) a
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
特别地:
-λa=-(λa) =λ(-a)
λ(a-b)=λa-λb
向量的加法、减法、数乘向量的综合运算叫向量的线性运算
练习1:若3m+2n=a,m-3n=b,其中a,b
是已知向量,求m,n.
-12a
5b
-a+5b-2c
例1 . 计算:
(1) (-3)×4a
(2) 3(a+b) –2(a-b)-a
(3) (2a+3b-c) –(3a-2b+c)
(4) (λ+μ)(a-b)-(λ-μ)(a+b)
2μa-2λb
例2.设x是未知向量,解方程
5(x+a)+3(x-b)=0
例3:已知向量
试说明
,
,
的关系。
A
B
C
D
E
A
B
D
E
C
解:
∴ 与 共线且同向.
AE
A
B
D
C
练习2.在⊿ABC中,设D为BC的中点,求证:
求证:AD= (AB+AC)
1
2
A
B
C
O
a b
,
a
b
OB=a+2b,OC=a+3b
练习3. 已知任意两个向量 ,试作
你能判断A、B、C三点之
间的位置关系吗?为什么?
、
OA=a+b
a
b
2
b
3
b
