8.3.1分类变量与列联表 课件——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共22张PPT)
文档属性
| 名称 | 8.3.1分类变量与列联表 课件——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 16:28:08 | ||
图片预览




文档简介
(共22张PPT)
数学
选择性必修第三册
第八章 成对数据的统计分析
8.3.1 分类变量与列联表
成语“名师出高徒”可以解释为“知名老师指导出高水平学生的概率较大”,即老师的名声与学生的水平之间有关联,你能举出更多的描述生活中两种属性或现象之间关联的词语吗
“虎父无犬子”
“强将手下无弱兵”
了解 探究分类变量之间关系的方法
制作、理解 2×2列联表,用频率分析法、图形分析法探究两个分类变量之间的关系
能够对统计数据进行简单整理、初步分析
提升数学抽象、数据建模及数据分析素养
学习目标
8.3.1 分类变量与列联表
情景引入
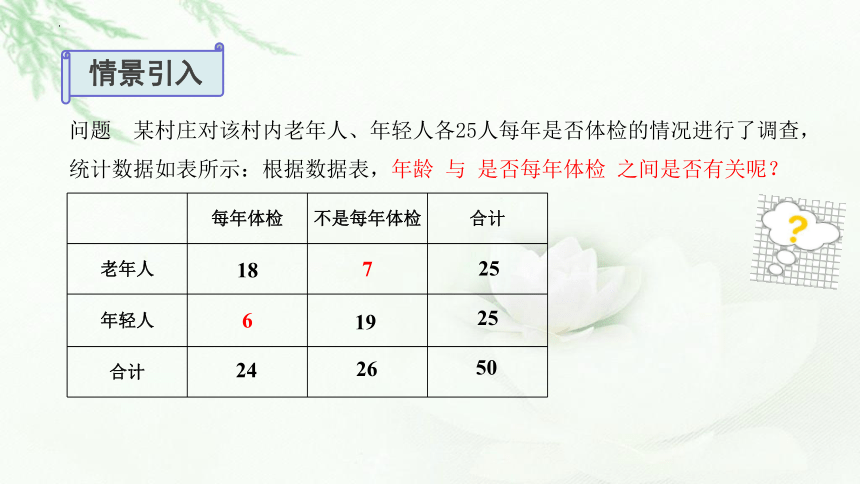
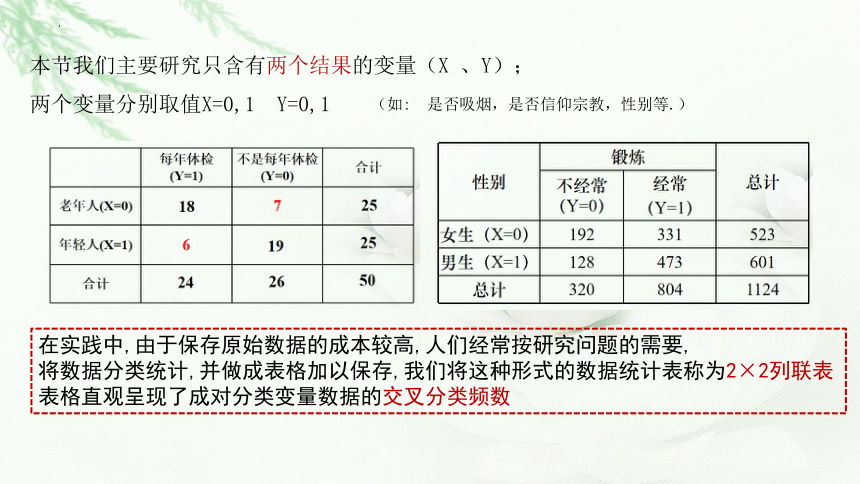
问题 某村庄对该村内老年人、年轻人各25人每年是否体检的情况进行了调查,统计数据如表所示:根据数据表,年龄 与 是否每年体检 之间是否有关呢?
每年体检 不是每年体检 合计
老年人 7
年轻人 6
合计
25
25
50
18
24
26
19
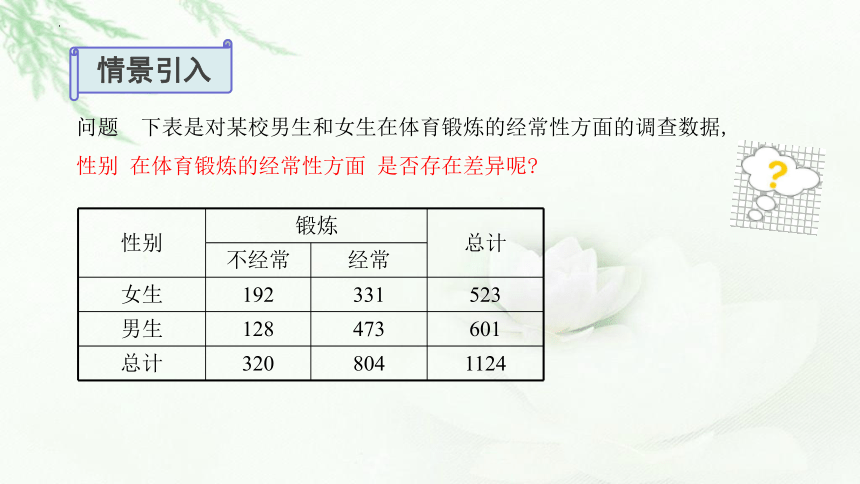
问题 下表是对某校男生和女生在体育锻炼的经常性方面的调查数据,
性别 在体育锻炼的经常性方面 是否存在差异呢
性别 锻炼 总计
不经常 经常
女生 192 331 523
男生 128 473 601
总计 320 804 1124
情景引入
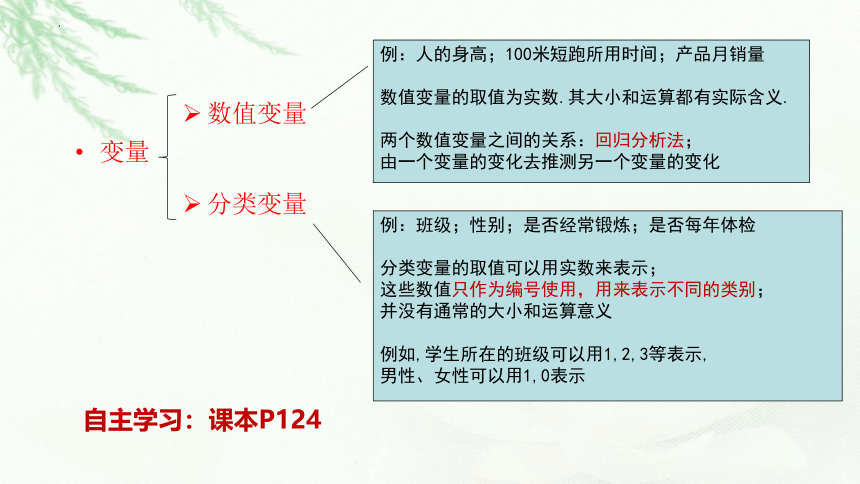
变量
数值变量
分类变量
什么是分类变量?
分类变量与数值变量之间的区别是什么?
自主学习:课本P124
变量
数值变量
分类变量
自主学习:课本P124
例:人的身高;100米短跑所用时间;产品月销量
数值变量的取值为实数.其大小和运算都有实际含义.
两个数值变量之间的关系:回归分析法;
由一个变量的变化去推测另一个变量的变化
例:班级;性别;是否经常锻炼;是否每年体检
分类变量的取值可以用实数来表示;
这些数值只作为编号使用,用来表示不同的类别;
并没有通常的大小和运算意义
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要研究只含有两个结果的变量(X 、Y);
两个变量分别取值X=0,1 Y=0,1
在实践中,由于保存原始数据的成本较高,人们经常按研究问题的需要,
将数据分类统计,并做成表格加以保存,我们将这种形式的数据统计表称为2×2列联表
表格直观呈现了成对分类变量数据的交叉分类频数
(如: 是否吸烟,是否信仰宗教,性别等.)
√
如何判断两个分类变量之间是否具有关联性呢?
问题探究
年龄 与 是否每年体检 之间是否有关呢?
性别 在体育锻炼的经常性方面 是否存在差异呢?
自主学习:课本P124-127
小组讨论,总结出三种判断方法
方法1——由频率估计概率
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
问题解决
性别 在体育锻炼的经常性方面 是否存在差异呢?
方法2——借助条件概率
性别 锻炼 总计
不经常(Y=0) 经常(Y=1)
女生(X=0) 192 331 523
男生(X=1) 128 473 601
总计 320 804 1124
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
性别 在体育锻炼的经常性方面 是否存在差异呢?
方法3——借助等高堆积条形图
性别 锻炼 总计
不经常(Y=0) 经常 (Y=1)
女生(X=0) 192 331 523
男生(X=1) 128 473 601
总计 320 804 1124
性别 在体育锻炼的经常性方面 是否存在差异呢?
自主学习:结合课本P126-127例1
理解等高堆积条形图
讨论此图有何特点?
牛刀小试:1.下列关于等高条形图的叙述正确的是( )
A.从等高条形图中可以精确地判断两个分类变量是否有关系
B.从等高条形图中可以看出两个变量频数的相对大小
C.从等高条形图中可以粗略地看出两个分类变量是否有关系
D.以上说法都不对
深入认识等高堆积条形图
在等高条形图中仅能粗略地判断两个分类变量的关系,故A错,C对.
在等高条形图中仅能够找出频率,无法找出频数,故B错.
牛刀小试:2.如图是调查某地区男女中学生是否喜欢理科的等高条形图,从图中可以看出该地区的中学生( )
A.性别与是否喜欢理科无关
B.女生中喜欢理科的比例为80%
C.男生比女生喜欢理科的可能性大
D.男生中喜欢理科的比例为80%
深入认识等高堆积条形图
牛刀小试:
深入认识等高堆积条形图
D
牛刀小试:
深入认识等高堆积条形图
4.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高堆积条形图:
当堂总结
2×2列联表 —— 给出了两个分类变量数据的交叉分类频数
判断两个分类变量之间是否具有关联性的三种方法
图形分析法
频率分析法
条件概率法
这样得出的结论是否会出现错误呢?是由什么引起的?
问题拓展:假设在本小节“问题”中,只是随机抽取了44名学生,按照性别和体育锻炼情况整理为如下的列联表:
(1)据此推断性别因素是否影响学生锻炼的经常性;
(2)说明你的推断结论是否可能犯错,并解释原因.
性别 锻炼 总计
不经常 经常
女生 5 15 20
男生 6 18 24
总计 11 33 44
因为“性别因素影响学生锻炼经常性”这个结论是根据两个频率间存在差异推断出来的.
在随机抽取的这个样本中,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.
因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算. 后面,我们将讨论犯这种错误的概率大小问题. 学习“独立性检验”.
对上述问题的思考
数学
选择性必修第三册
第八章 成对数据的统计分析
8.3.1 分类变量与列联表
成语“名师出高徒”可以解释为“知名老师指导出高水平学生的概率较大”,即老师的名声与学生的水平之间有关联,你能举出更多的描述生活中两种属性或现象之间关联的词语吗
“虎父无犬子”
“强将手下无弱兵”
了解 探究分类变量之间关系的方法
制作、理解 2×2列联表,用频率分析法、图形分析法探究两个分类变量之间的关系
能够对统计数据进行简单整理、初步分析
提升数学抽象、数据建模及数据分析素养
学习目标
8.3.1 分类变量与列联表
情景引入
问题 某村庄对该村内老年人、年轻人各25人每年是否体检的情况进行了调查,统计数据如表所示:根据数据表,年龄 与 是否每年体检 之间是否有关呢?
每年体检 不是每年体检 合计
老年人 7
年轻人 6
合计
25
25
50
18
24
26
19
问题 下表是对某校男生和女生在体育锻炼的经常性方面的调查数据,
性别 在体育锻炼的经常性方面 是否存在差异呢
性别 锻炼 总计
不经常 经常
女生 192 331 523
男生 128 473 601
总计 320 804 1124
情景引入
变量
数值变量
分类变量
什么是分类变量?
分类变量与数值变量之间的区别是什么?
自主学习:课本P124
变量
数值变量
分类变量
自主学习:课本P124
例:人的身高;100米短跑所用时间;产品月销量
数值变量的取值为实数.其大小和运算都有实际含义.
两个数值变量之间的关系:回归分析法;
由一个变量的变化去推测另一个变量的变化
例:班级;性别;是否经常锻炼;是否每年体检
分类变量的取值可以用实数来表示;
这些数值只作为编号使用,用来表示不同的类别;
并没有通常的大小和运算意义
例如,学生所在的班级可以用1,2,3等表示,
男性、女性可以用1,0表示
本节我们主要研究只含有两个结果的变量(X 、Y);
两个变量分别取值X=0,1 Y=0,1
在实践中,由于保存原始数据的成本较高,人们经常按研究问题的需要,
将数据分类统计,并做成表格加以保存,我们将这种形式的数据统计表称为2×2列联表
表格直观呈现了成对分类变量数据的交叉分类频数
(如: 是否吸烟,是否信仰宗教,性别等.)
√
如何判断两个分类变量之间是否具有关联性呢?
问题探究
年龄 与 是否每年体检 之间是否有关呢?
性别 在体育锻炼的经常性方面 是否存在差异呢?
自主学习:课本P124-127
小组讨论,总结出三种判断方法
方法1——由频率估计概率
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
问题解决
性别 在体育锻炼的经常性方面 是否存在差异呢?
方法2——借助条件概率
性别 锻炼 总计
不经常(Y=0) 经常(Y=1)
女生(X=0) 192 331 523
男生(X=1) 128 473 601
总计 320 804 1124
结论:该校的女生和男生在体育锻炼的经常性方面存在差异,男生更经常锻炼。
性别 在体育锻炼的经常性方面 是否存在差异呢?
方法3——借助等高堆积条形图
性别 锻炼 总计
不经常(Y=0) 经常 (Y=1)
女生(X=0) 192 331 523
男生(X=1) 128 473 601
总计 320 804 1124
性别 在体育锻炼的经常性方面 是否存在差异呢?
自主学习:结合课本P126-127例1
理解等高堆积条形图
讨论此图有何特点?
牛刀小试:1.下列关于等高条形图的叙述正确的是( )
A.从等高条形图中可以精确地判断两个分类变量是否有关系
B.从等高条形图中可以看出两个变量频数的相对大小
C.从等高条形图中可以粗略地看出两个分类变量是否有关系
D.以上说法都不对
深入认识等高堆积条形图
在等高条形图中仅能粗略地判断两个分类变量的关系,故A错,C对.
在等高条形图中仅能够找出频率,无法找出频数,故B错.
牛刀小试:2.如图是调查某地区男女中学生是否喜欢理科的等高条形图,从图中可以看出该地区的中学生( )
A.性别与是否喜欢理科无关
B.女生中喜欢理科的比例为80%
C.男生比女生喜欢理科的可能性大
D.男生中喜欢理科的比例为80%
深入认识等高堆积条形图
牛刀小试:
深入认识等高堆积条形图
D
牛刀小试:
深入认识等高堆积条形图
4.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高堆积条形图:
当堂总结
2×2列联表 —— 给出了两个分类变量数据的交叉分类频数
判断两个分类变量之间是否具有关联性的三种方法
图形分析法
频率分析法
条件概率法
这样得出的结论是否会出现错误呢?是由什么引起的?
问题拓展:假设在本小节“问题”中,只是随机抽取了44名学生,按照性别和体育锻炼情况整理为如下的列联表:
(1)据此推断性别因素是否影响学生锻炼的经常性;
(2)说明你的推断结论是否可能犯错,并解释原因.
性别 锻炼 总计
不经常 经常
女生 5 15 20
男生 6 18 24
总计 11 33 44
因为“性别因素影响学生锻炼经常性”这个结论是根据两个频率间存在差异推断出来的.
在随机抽取的这个样本中,因为频率具有随机性,频率与概率之间存在误差,所以我们的推断可能犯错误,而且在样本容量较小时,犯错误的可能性会较大.
因此,需要找到一种更为合理的推断方法,同时也希望能对出现错误推断的概率有一定的控制或估算. 后面,我们将讨论犯这种错误的概率大小问题. 学习“独立性检验”.
对上述问题的思考
