6.1.2向量的加法 课件(共23张PPT)
文档属性
| 名称 | 6.1.2向量的加法 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 736.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 11:37:21 | ||
图片预览

文档简介
(共23张PPT)
向量的加法
复习回顾
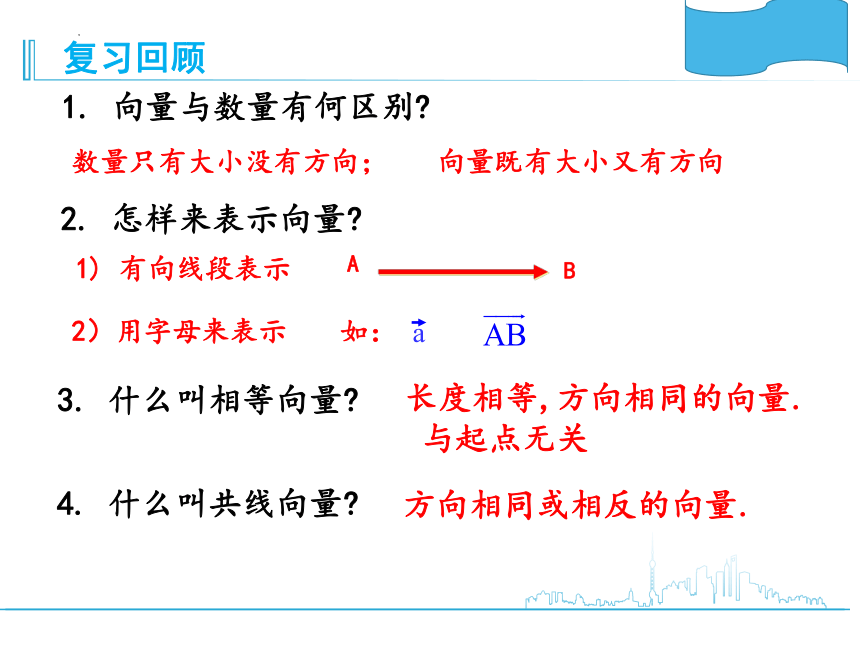
1. 向量与数量有何区别
数量只有大小没有方向;
向量既有大小又有方向
2. 怎样来表示向量
1) 有向线段表示
2)用字母来表示
如:
A
B
a
3. 什么叫相等向量
长度相等,方向相同的向量.
与起点无关
4. 什么叫共线向量
方向相同或相反的向量.
创设情境 直观感知
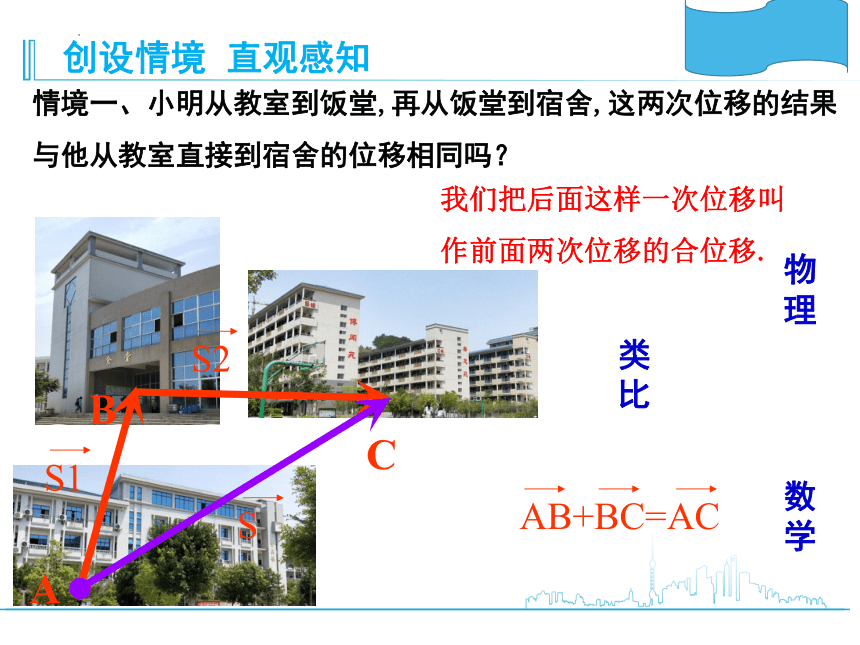
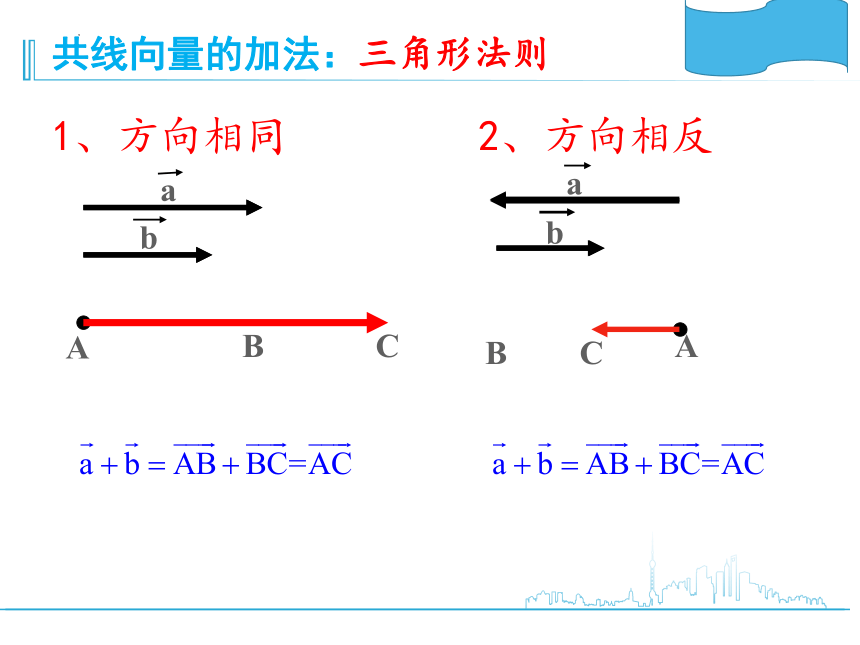
AB+BC=AC
情境一、小明从教室到饭堂,再从饭堂到宿舍,这两次位移的结果与他从教室直接到宿舍的位移相同吗?
我们把后面这样一次位移叫作前面两次位移的合位移.
物理
数学
类比
A
B
C
S1
S2
S
探究归纳 形成概念
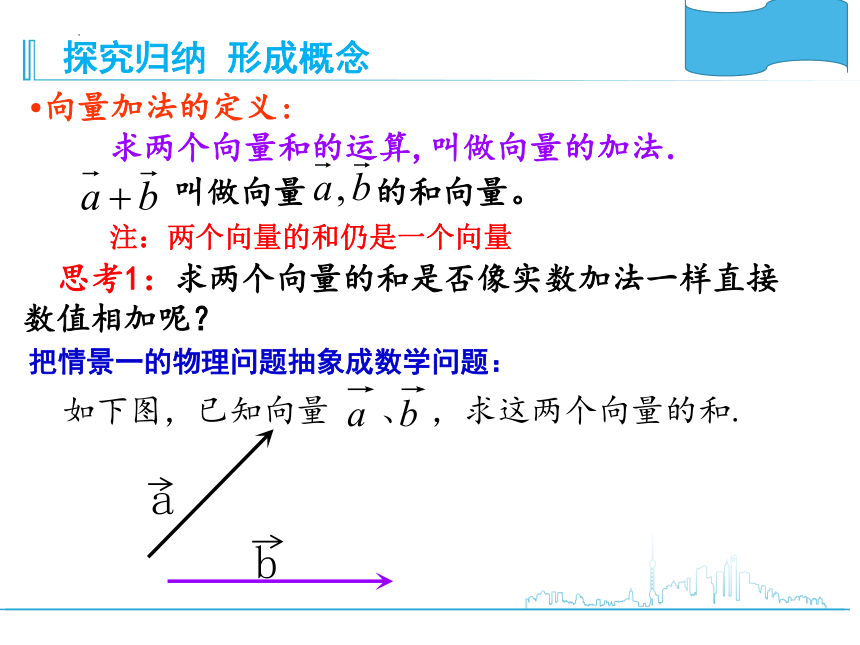
求两个向量和的运算,叫做向量的加法.
向量加法的定义:
把情景一的物理问题抽象成数学问题:
思考1:求两个向量的和是否像实数加法一样直接数值相加呢?
如下图,已知向量 、 ,求这两个向量的和.
注:两个向量的和仍是一个向量
a
b
叫做向量 的和向量。
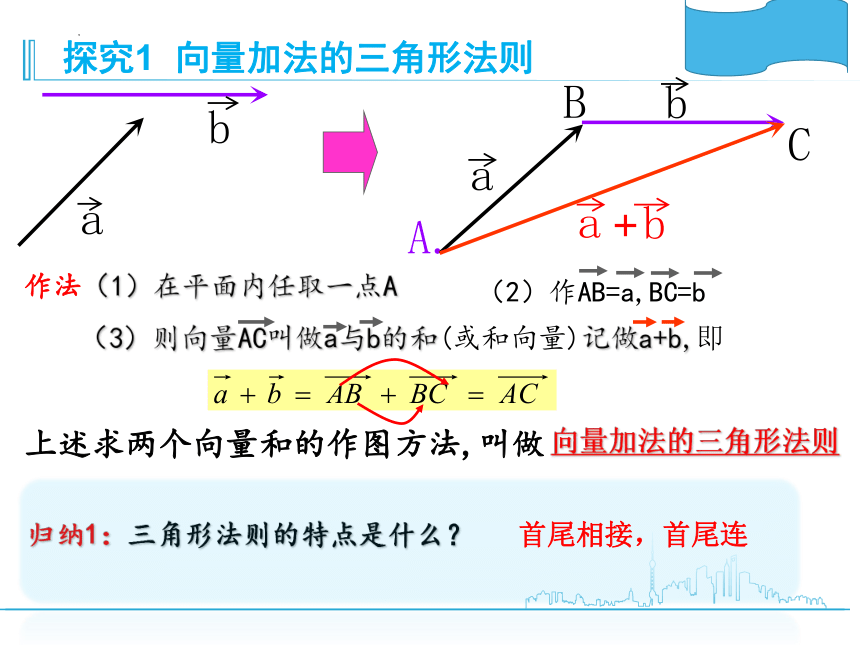
(3)则向量AC叫做a与b的和(或和向量)记做a+b,即
作法(1)在平面内任取一点A
归纳1:三角形法则的特点是什么?
(2)作AB=a,BC=b
探究1 向量加法的三角形法则
上述求两个向量和的作图方法,叫做
向量加法的三角形法则
首尾相接,首尾连
A.
B
a
C
b
b
a
+
a
b
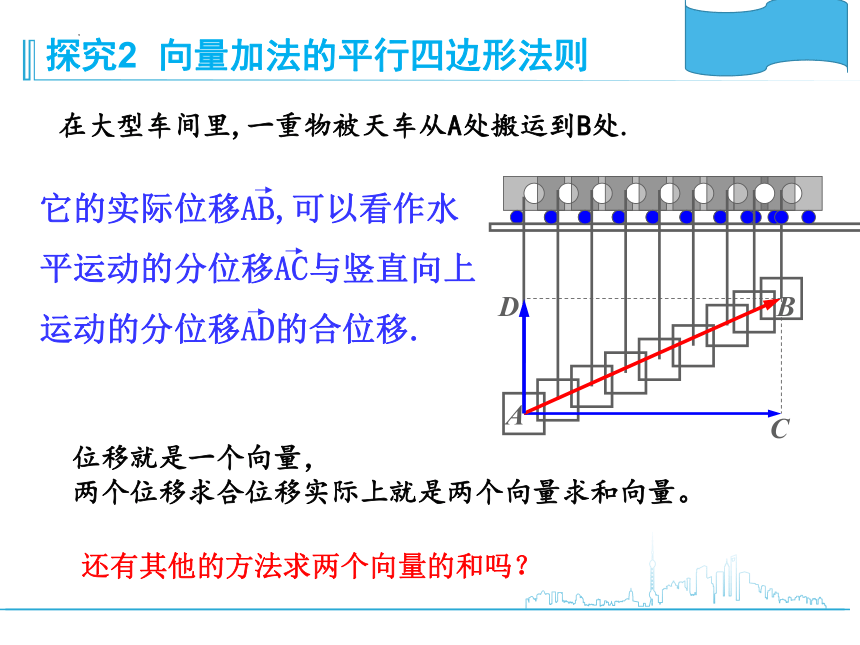
在大型车间里,一重物被天车从A处搬运到B处.
它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.
位移就是一个向量,
两个位移求合位移实际上就是两个向量求和向量。
探究2 向量加法的平行四边形法则
还有其他的方法求两个向量的和吗?
C
A
B
D
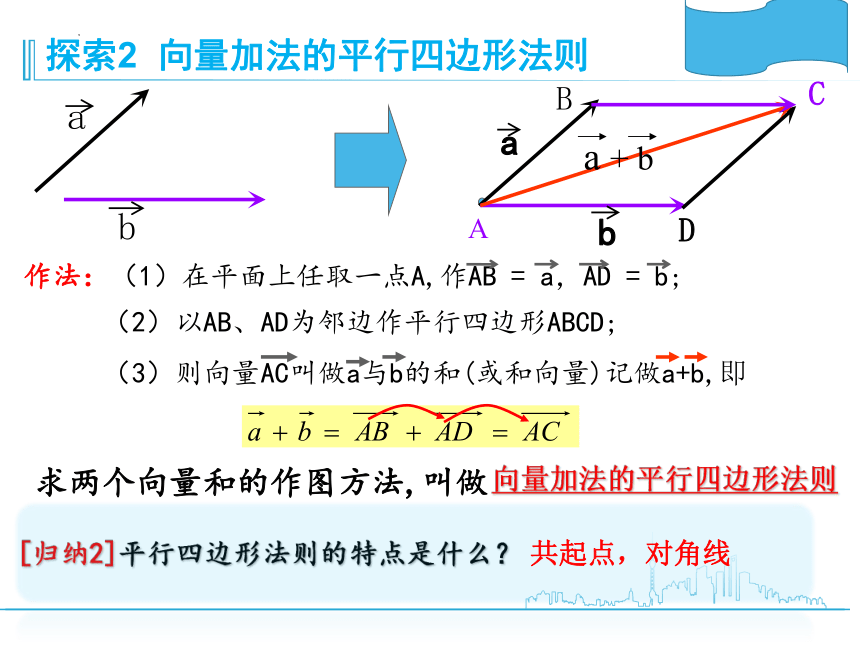
探索2 向量加法的平行四边形法则
(2)以AB、AD为邻边作平行四边形ABCD;
作法:(1)在平面上任取一点A,作AB = a,AD = b;
a
b
A
a
B
b
D
C
a + b
(3)则向量AC叫做a与b的和(或和向量)记做a+b,即
[归纳2]平行四边形法则的特点是什么?
求两个向量和的作图方法,叫做
向量加法的平行四边形法则
共起点,对角线
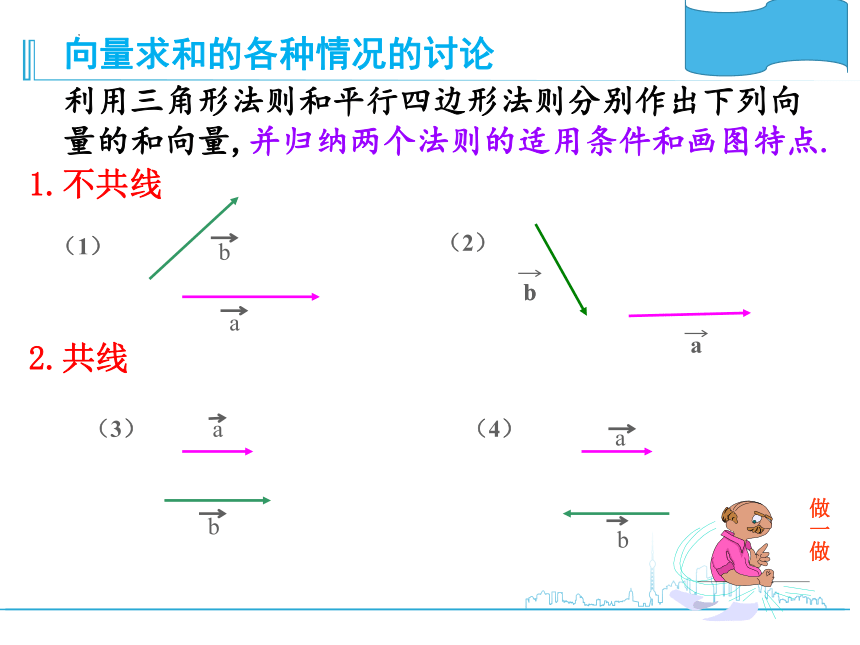
利用三角形法则和平行四边形法则分别作出下列向量的和向量,并归纳两个法则的适用条件和画图特点.
a
b
b
(1)
(2)
(4)
(3)
a
b
b
a
a
b
做一做
向量求和的各种情况的讨论
1.不共线
2.共线
共线向量的加法:
A
B
C
C
B
A
2、方向相反
b
a
1、方向相同
a
b
三角形法则
b
b
a
b
a
三 角 形 法 则:
平行四边形法则:
A
C
B
a + b
B
O
A
C
a + b
归纳整理 总结特征
3.只适用于不共线向量的加法
3.适用于任意向量的加法,说明三角形更具有广泛性
1.将向量平移使得它们首尾相连.
2.和向量即是第一个向量的起点指向第二个向量的终点.
1.将向量平移到同一起点.
2.和向量即以它们作为邻边
平行四边形的共起点的对角线
A
B
C
D
(2) + =
O
(1) + =
1.填空.已知 ,
求下列向量之和.
跟踪练习1
DA
CB
实数的加法
向量的加法
性
质
交换律
结合律
?
?
实数的加法满足交换律与结合律.那么,向量的加法
是否也有类似的运算律呢?
类比猜想:
探索3 向量加法的运算律
A
B
C
D
b
r
实数的加法
向量的加法
性
质
交换律
结合律
?
?
探索3 向量加法的运算律
B
b
A
O
a
C
c
b
a
+
+
c
c
b
+
b
a
+
A1
A2
A3
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A2+A2A3= _______
A1A3
A1A4
多边形法则:n个向量的和等于折线起点到终点的向量
探究4:能否将它推广至多个向量的求和?
引申:
1.A1A2 + A2A3 +……+ An-1An =
A1An
2.
2. 化简
1. 根据图示填空
A
B
D
E
C
小试牛刀3
例1 轮船从A港沿东偏北 30°方向行驶了40 n mile(海里)
到达B处,再由B处沿正北方向行驶40 n mile到达C处.
求此时轮船与A港的相对位置.
北
A
B
30
D
东
C
实际应用
解:
如图,设 分别表示轮船的两次位移,
则 表示轮船的合位移,
在Rt△ADB中,∠ADB=90o,∠DAB=30o,
在Rt△AD中,∠ADC=90o,
答:轮船此时位移A港东偏北60o,且距A港
的C处.
40
40
?
?
?
例2 两个力F1和F2同时作用在一个物体上,其中F1=40N,方向向东,F2=30N,方向向北,求它们的合力.
东
北
O
θ
C
A
B
F1
F2
解:
如图,设 表示F1 , 表示F2 .
作平行四边形OACB,则 表示合力F.
由勾股定理,得
设合力F与力F1的夹角为θ,则
答:合力大小为50N,方向为东偏北约37o.
在Rt△OAC中,
实际应用
?
?
40
40
1. 根据图示填空
A
B
D
E
C
课堂练习
AC
AD
AD
AE
2.一架飞机向西飞行 ,
然后改变方向向南飞行 ,
则飞机两次位移的和为 ;
向西南方向飞行
课堂练习
南
西
平行四边形法则:
共起点,对角线
适用于不共线向量的加法
三角形法则:
首尾相接,首尾连
适用于任意向量的加法
不共线向量
任意向量
1.向量加法的定义
2.运算法则:
小结
3.实际应用
作业
课本P79 第 1.2 题
P81 第 2.3 题
O
B
A
1. 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
C
解:如图,设 表示小船垂直于河
岸行驶的速度, 表示水流的速度,
以OA,OB为邻边作平行四边形OABC,
则 就是小船实际航行的速度.
v1
v2
课后练习
变式:若要使小船沿垂直河岸方向到达对岸码头的实际速度的大小为了 km/h,
问:小船行驶的速度的大小和方向又该如何?
思考提升
向量的加法
复习回顾
1. 向量与数量有何区别
数量只有大小没有方向;
向量既有大小又有方向
2. 怎样来表示向量
1) 有向线段表示
2)用字母来表示
如:
A
B
a
3. 什么叫相等向量
长度相等,方向相同的向量.
与起点无关
4. 什么叫共线向量
方向相同或相反的向量.
创设情境 直观感知
AB+BC=AC
情境一、小明从教室到饭堂,再从饭堂到宿舍,这两次位移的结果与他从教室直接到宿舍的位移相同吗?
我们把后面这样一次位移叫作前面两次位移的合位移.
物理
数学
类比
A
B
C
S1
S2
S
探究归纳 形成概念
求两个向量和的运算,叫做向量的加法.
向量加法的定义:
把情景一的物理问题抽象成数学问题:
思考1:求两个向量的和是否像实数加法一样直接数值相加呢?
如下图,已知向量 、 ,求这两个向量的和.
注:两个向量的和仍是一个向量
a
b
叫做向量 的和向量。
(3)则向量AC叫做a与b的和(或和向量)记做a+b,即
作法(1)在平面内任取一点A
归纳1:三角形法则的特点是什么?
(2)作AB=a,BC=b
探究1 向量加法的三角形法则
上述求两个向量和的作图方法,叫做
向量加法的三角形法则
首尾相接,首尾连
A.
B
a
C
b
b
a
+
a
b
在大型车间里,一重物被天车从A处搬运到B处.
它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.
位移就是一个向量,
两个位移求合位移实际上就是两个向量求和向量。
探究2 向量加法的平行四边形法则
还有其他的方法求两个向量的和吗?
C
A
B
D
探索2 向量加法的平行四边形法则
(2)以AB、AD为邻边作平行四边形ABCD;
作法:(1)在平面上任取一点A,作AB = a,AD = b;
a
b
A
a
B
b
D
C
a + b
(3)则向量AC叫做a与b的和(或和向量)记做a+b,即
[归纳2]平行四边形法则的特点是什么?
求两个向量和的作图方法,叫做
向量加法的平行四边形法则
共起点,对角线
利用三角形法则和平行四边形法则分别作出下列向量的和向量,并归纳两个法则的适用条件和画图特点.
a
b
b
(1)
(2)
(4)
(3)
a
b
b
a
a
b
做一做
向量求和的各种情况的讨论
1.不共线
2.共线
共线向量的加法:
A
B
C
C
B
A
2、方向相反
b
a
1、方向相同
a
b
三角形法则
b
b
a
b
a
三 角 形 法 则:
平行四边形法则:
A
C
B
a + b
B
O
A
C
a + b
归纳整理 总结特征
3.只适用于不共线向量的加法
3.适用于任意向量的加法,说明三角形更具有广泛性
1.将向量平移使得它们首尾相连.
2.和向量即是第一个向量的起点指向第二个向量的终点.
1.将向量平移到同一起点.
2.和向量即以它们作为邻边
平行四边形的共起点的对角线
A
B
C
D
(2) + =
O
(1) + =
1.填空.已知 ,
求下列向量之和.
跟踪练习1
DA
CB
实数的加法
向量的加法
性
质
交换律
结合律
?
?
实数的加法满足交换律与结合律.那么,向量的加法
是否也有类似的运算律呢?
类比猜想:
探索3 向量加法的运算律
A
B
C
D
b
r
实数的加法
向量的加法
性
质
交换律
结合律
?
?
探索3 向量加法的运算律
B
b
A
O
a
C
c
b
a
+
+
c
c
b
+
b
a
+
A1
A2
A3
A1
A2
A3
A4
A1A2+A2A3+A3A4=_______
A1A2+A2A3= _______
A1A3
A1A4
多边形法则:n个向量的和等于折线起点到终点的向量
探究4:能否将它推广至多个向量的求和?
引申:
1.A1A2 + A2A3 +……+ An-1An =
A1An
2.
2. 化简
1. 根据图示填空
A
B
D
E
C
小试牛刀3
例1 轮船从A港沿东偏北 30°方向行驶了40 n mile(海里)
到达B处,再由B处沿正北方向行驶40 n mile到达C处.
求此时轮船与A港的相对位置.
北
A
B
30
D
东
C
实际应用
解:
如图,设 分别表示轮船的两次位移,
则 表示轮船的合位移,
在Rt△ADB中,∠ADB=90o,∠DAB=30o,
在Rt△AD中,∠ADC=90o,
答:轮船此时位移A港东偏北60o,且距A港
的C处.
40
40
?
?
?
例2 两个力F1和F2同时作用在一个物体上,其中F1=40N,方向向东,F2=30N,方向向北,求它们的合力.
东
北
O
θ
C
A
B
F1
F2
解:
如图,设 表示F1 , 表示F2 .
作平行四边形OACB,则 表示合力F.
由勾股定理,得
设合力F与力F1的夹角为θ,则
答:合力大小为50N,方向为东偏北约37o.
在Rt△OAC中,
实际应用
?
?
40
40
1. 根据图示填空
A
B
D
E
C
课堂练习
AC
AD
AD
AE
2.一架飞机向西飞行 ,
然后改变方向向南飞行 ,
则飞机两次位移的和为 ;
向西南方向飞行
课堂练习
南
西
平行四边形法则:
共起点,对角线
适用于不共线向量的加法
三角形法则:
首尾相接,首尾连
适用于任意向量的加法
不共线向量
任意向量
1.向量加法的定义
2.运算法则:
小结
3.实际应用
作业
课本P79 第 1.2 题
P81 第 2.3 题
O
B
A
1. 在小船过河时,小船沿垂直河岸方向行驶的速度为v1= km/h,河水流动的速度v2=2.0km/h
求小船过河实际航行速度的大小和方向.
C
解:如图,设 表示小船垂直于河
岸行驶的速度, 表示水流的速度,
以OA,OB为邻边作平行四边形OABC,
则 就是小船实际航行的速度.
v1
v2
课后练习
变式:若要使小船沿垂直河岸方向到达对岸码头的实际速度的大小为了 km/h,
问:小船行驶的速度的大小和方向又该如何?
思考提升
