6.4.3余弦定理 课件(共23张PPT)
文档属性
| 名称 | 6.4.3余弦定理 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 528.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 09:38:39 | ||
图片预览








文档简介
(共23张PPT)
6.4.3 余弦定理
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积等,它们之间存在着确定的关系,例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.对于一般三角形,我们已经定性地研究过三角形的边、角关系,得到了SSS,SAS,ASA,AAS等判定三角形全等的方法,这些判定方法表明,给定三角形的三个角、三条边这六个元素中的某些元素,这个三角形就是唯一确定的。
那么三角形的其他元素与给定的某些元素有怎样的数量关系?
新课引入
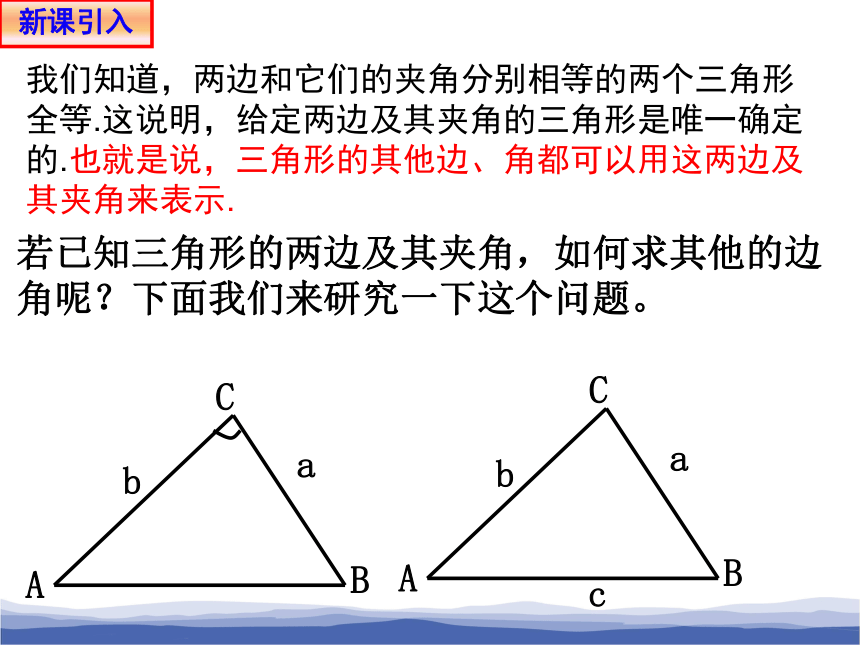
若已知三角形的两边及其夹角,如何求其他的边角呢?下面我们来研究一下这个问题。
C
A
B
a
b
C
A
B
a
b
c
新课引入
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的.也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.
新课引入
在△ABC中,若已知边a,b和它们的夹角C,求第三条边c.
C
A
B
a
b
c
学习新知
余弦定理:
三角形中任何一边的平方,等于其他两边的平方和,减去这两边与其夹角的余弦的积的两倍.
学习新知
余弦定理的主要作用:
(1)已知两边一角求边;(SAS)
(2)已知三边求角.(SSS)
学习新知
例1. 在△ABC中,已知a= cm,
c= cm,B=45°,解三角形.
步骤:
1.求第三边;(余弦定理)
2.求已知边中较小边所对的角;
3.求第三角(内角和为π)
已知两边及夹角求边;(SAS)
典型例题
巩固练习
例2. 在△ABC中,已知 ,
,求最大角.
已知三边求角.(SSS)
典型例题
已知三角形三边求角,可先用余弦定理求两个角,进而求出第三个角.
【思路点拨】 在三角形中,大边对大角,所以a边所对角最大,然后根据已知三边可用余弦定理求三角.
在△ABC中,已知a=7,b=3,c=5,
求最大角
巩固练习
例3 在△ABC中,角A、B、C的对边分
别为a 、b 、c,若AB AC=BA BC=1.
(1)求证:A=B;
(2)求边长c的值.
(3)若|AB+AC|= ,求△ABC的面积.
典型例题
训练
1.在△ABC中:
(1)已知b=8,c=3,A=60°,求a;
(2)已知a=20,b=29,c=21,求B;
(3)已知a=3 ,c=2,B=150°,求b;
(4)已知a=2,b= 求A
巩固练习
典型例题
典型例题
在△ABC中,acos A+bcos B=ccos C,试判断三角形的形状.
【思路点拨】 利用余弦定理把边与角的关系转化为边与边的关系.
通分整理得:
a2(b2+c2-a2)+b2(a2+c2-b2)+c2(c2-a2-b2)=0.
展开整理得(a2-b2)2=c4.
∴a2-b2=±c2,即a2=b2+c2或b2=a2+c2.
根据勾股定理,知△ABC是直角三角形.
方法总结
判断三角形的形状
判断三角形的形状应围绕三角形的边角关系进行思考,可用余弦定理将已知条件转化为边边关系,通过因式分解、配方等方式得出边的相应关系,从而判断三角形的形状,也可利用余弦定理将已知条件转化为角与角之间的关系,通过三角变换,得出三角形各内角之间的关系,从而判断三角形形状.
巩固练习
在△ABC中, bcos A=acos B ,试判断三角形的形状.
巩固练习
巩固练习
1.余弦定理的主要作用是已知两边一角求边,或已知三边求角,所得结论是唯一的.同时,利用余弦定理也可以实现边角转化.
2.余弦定理及其推论共有六个基本公式,应用时要注意适当选取,有时可结合正弦定理求解.
课堂小结
1.余弦定理指出了三角形的三条边与其中的一个角之间的关系,每一个等式中都包含四个不同的量,它们分别是三角形的三边和一个角,知道其中的三个量,就可以求得第四个量:
(1)已知两边与它们的夹角,可以求得第三边;
(2)已知两边与其中一边的对角,可以代入余弦定理,看成关于另一边的二次方程,从而解得另一边;
(3)已知三角形的三边可以求得三角形的三个角.从这里可以看出,利用余弦定理解三角形时,条件中必须至少知道两边.
课堂小结
2.余弦定理与勾股定理
余弦定理可以看作是勾股定理的推广,勾股定理可以看作是余弦定理的特例.
(1)如果一个三角形两边的平方和大于第三边的平方,那么第三边所对的角是锐角.
(2)如果一个三角形两边的平方和小于第三边的平方,那么第三边所对的角是钝角.
(3)如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角是直角.
课堂小结
6.4.3 余弦定理
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积等,它们之间存在着确定的关系,例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.对于一般三角形,我们已经定性地研究过三角形的边、角关系,得到了SSS,SAS,ASA,AAS等判定三角形全等的方法,这些判定方法表明,给定三角形的三个角、三条边这六个元素中的某些元素,这个三角形就是唯一确定的。
那么三角形的其他元素与给定的某些元素有怎样的数量关系?
新课引入
若已知三角形的两边及其夹角,如何求其他的边角呢?下面我们来研究一下这个问题。
C
A
B
a
b
C
A
B
a
b
c
新课引入
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的.也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.
新课引入
在△ABC中,若已知边a,b和它们的夹角C,求第三条边c.
C
A
B
a
b
c
学习新知
余弦定理:
三角形中任何一边的平方,等于其他两边的平方和,减去这两边与其夹角的余弦的积的两倍.
学习新知
余弦定理的主要作用:
(1)已知两边一角求边;(SAS)
(2)已知三边求角.(SSS)
学习新知
例1. 在△ABC中,已知a= cm,
c= cm,B=45°,解三角形.
步骤:
1.求第三边;(余弦定理)
2.求已知边中较小边所对的角;
3.求第三角(内角和为π)
已知两边及夹角求边;(SAS)
典型例题
巩固练习
例2. 在△ABC中,已知 ,
,求最大角.
已知三边求角.(SSS)
典型例题
已知三角形三边求角,可先用余弦定理求两个角,进而求出第三个角.
【思路点拨】 在三角形中,大边对大角,所以a边所对角最大,然后根据已知三边可用余弦定理求三角.
在△ABC中,已知a=7,b=3,c=5,
求最大角
巩固练习
例3 在△ABC中,角A、B、C的对边分
别为a 、b 、c,若AB AC=BA BC=1.
(1)求证:A=B;
(2)求边长c的值.
(3)若|AB+AC|= ,求△ABC的面积.
典型例题
训练
1.在△ABC中:
(1)已知b=8,c=3,A=60°,求a;
(2)已知a=20,b=29,c=21,求B;
(3)已知a=3 ,c=2,B=150°,求b;
(4)已知a=2,b= 求A
巩固练习
典型例题
典型例题
在△ABC中,acos A+bcos B=ccos C,试判断三角形的形状.
【思路点拨】 利用余弦定理把边与角的关系转化为边与边的关系.
通分整理得:
a2(b2+c2-a2)+b2(a2+c2-b2)+c2(c2-a2-b2)=0.
展开整理得(a2-b2)2=c4.
∴a2-b2=±c2,即a2=b2+c2或b2=a2+c2.
根据勾股定理,知△ABC是直角三角形.
方法总结
判断三角形的形状
判断三角形的形状应围绕三角形的边角关系进行思考,可用余弦定理将已知条件转化为边边关系,通过因式分解、配方等方式得出边的相应关系,从而判断三角形的形状,也可利用余弦定理将已知条件转化为角与角之间的关系,通过三角变换,得出三角形各内角之间的关系,从而判断三角形形状.
巩固练习
在△ABC中, bcos A=acos B ,试判断三角形的形状.
巩固练习
巩固练习
1.余弦定理的主要作用是已知两边一角求边,或已知三边求角,所得结论是唯一的.同时,利用余弦定理也可以实现边角转化.
2.余弦定理及其推论共有六个基本公式,应用时要注意适当选取,有时可结合正弦定理求解.
课堂小结
1.余弦定理指出了三角形的三条边与其中的一个角之间的关系,每一个等式中都包含四个不同的量,它们分别是三角形的三边和一个角,知道其中的三个量,就可以求得第四个量:
(1)已知两边与它们的夹角,可以求得第三边;
(2)已知两边与其中一边的对角,可以代入余弦定理,看成关于另一边的二次方程,从而解得另一边;
(3)已知三角形的三边可以求得三角形的三个角.从这里可以看出,利用余弦定理解三角形时,条件中必须至少知道两边.
课堂小结
2.余弦定理与勾股定理
余弦定理可以看作是勾股定理的推广,勾股定理可以看作是余弦定理的特例.
(1)如果一个三角形两边的平方和大于第三边的平方,那么第三边所对的角是锐角.
(2)如果一个三角形两边的平方和小于第三边的平方,那么第三边所对的角是钝角.
(3)如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角是直角.
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
