8.3.2圆柱圆锥圆台球表面积和体积 课件(共24张PPT)
文档属性
| 名称 | 8.3.2圆柱圆锥圆台球表面积和体积 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 854.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
8.3.2 圆柱圆锥圆台球表面积和体积
(1)矩形面积公式: __________。
(2)圆面积公式: _________。
(3)圆周长公式: _________。
(4)扇形面积公式: _ _________。
复习引入
多面体的表面积
就是围成多面体各个面的面积之和
棱柱的体积
棱锥的体积
棱台的体积
思考
如何根据圆柱,圆锥的几何结构特征,求它们的表面积
与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。
利用圆柱、圆锥、圆台的展开图,可以得到它们的表面积公式
新课引入
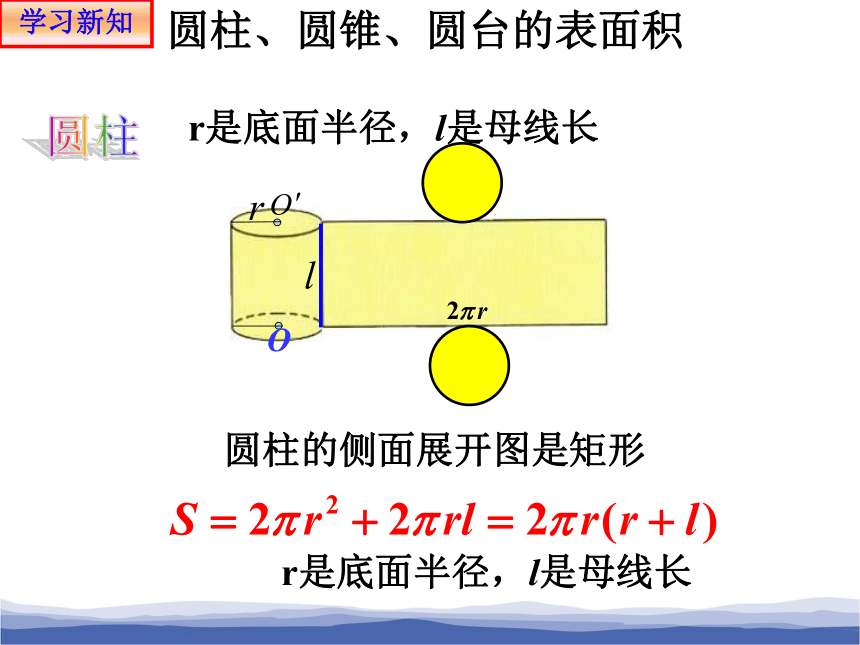
圆柱的侧面展开图是矩形
O
圆柱
圆柱、圆锥、圆台的表面积
学习新知
r是底面半径,l是母线长
r是底面半径,l是母线长
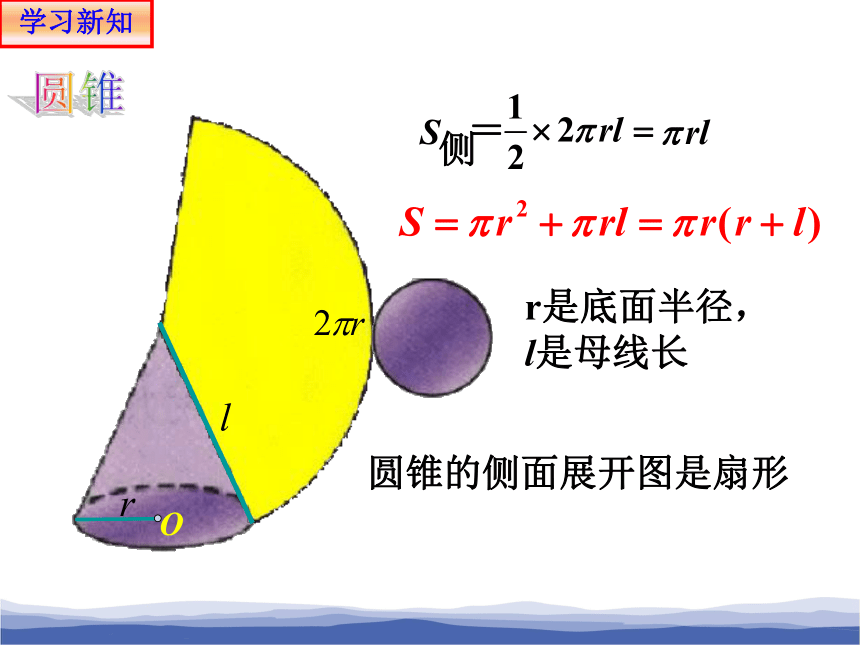
圆锥的侧面展开图是扇形
O
侧
=
圆锥
学习新知
r是底面半径,
l是母线长
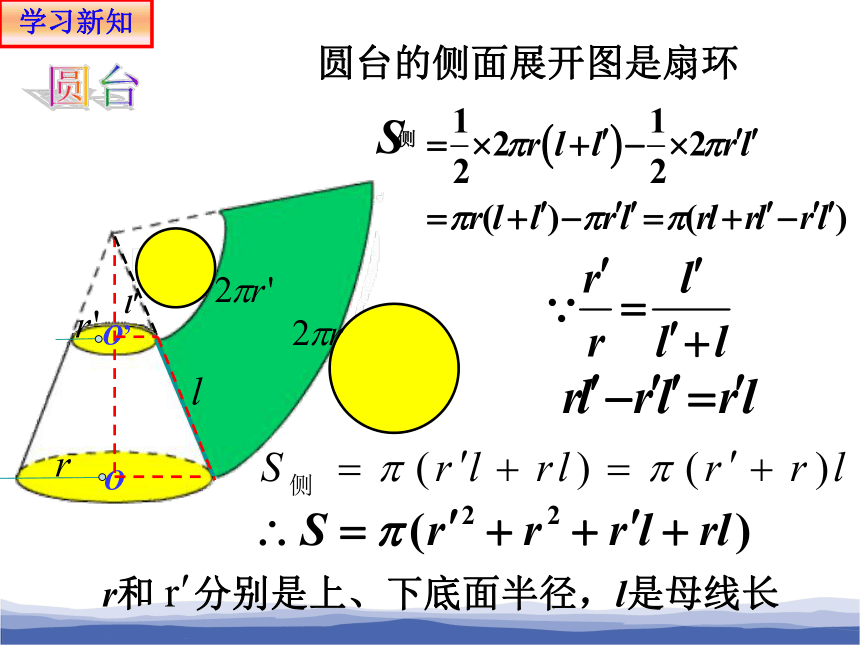
O
O’
圆台的侧面展开图是扇环
圆台
侧
学习新知
r和 分别是上、下底面半径,l是母线长
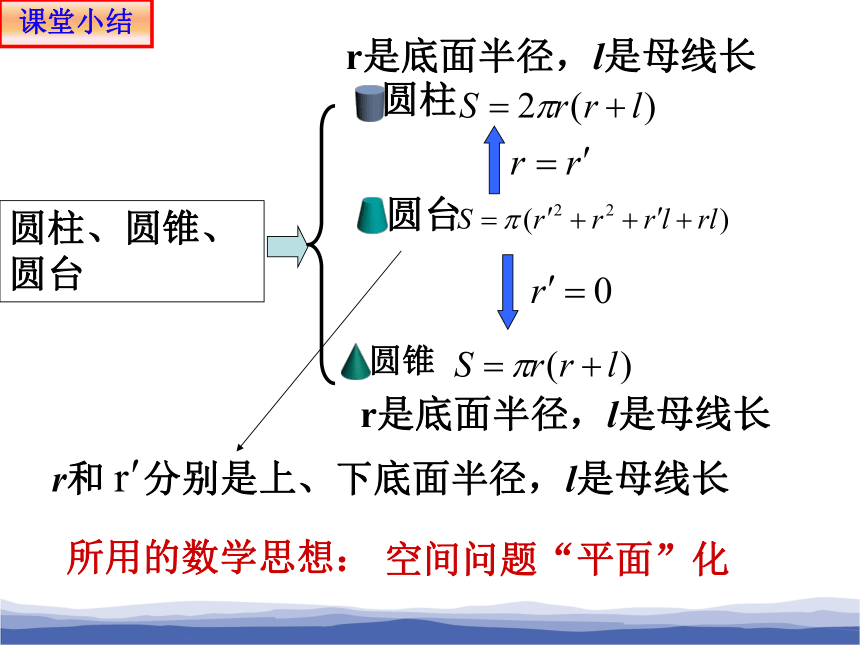
圆台
圆柱
圆锥
空间问题“平面”化
圆柱、圆锥、圆台
所用的数学思想:
课堂小结
r是底面半径,l是母线长
r是底面半径,l是母线长
r和 分别是上、下底面半径,l是母线长
圆柱的体积:
圆锥的体积:
体积:几何体所占空间的大小
复习回顾
V棱柱=Sh.
棱柱的体积:
棱锥的体积:
棱台的体积:
圆台的体积:
关于体积有如下几个原理:
(1)相同的几何体的体积相等;
(2)一个几何体的体积等于它的各部分体积之和; (3)等底面积等高的两个同类几何体的体积相等; (4)体积相等的两个几何体叫做等积体.
学习新知
柱体、锥体、台体的体积
锥体
台体
柱体
柱体、锥体、
台体的体积
知识总结
球的表面积公式
半径是R的球的表面积是
S=4 R2
小学,,我们学习了圆的面积公式,你还记得是如何求得的吗
类比这种方法你能由球的表面积公式推导出球的体积公式
学习新知
第一步:分割
O
球面被分割成n个网格,
表面积分别为:
则球的表面积:
则球的体积为:
设“小锥体”的体积为:
O
球的体积公式
学习新知
O
第二步:求近似和
O
由第一步得:
学习新知
第三步:转化为球的体积
如果网格分的越细,则:
①
由①② 得:
②
球的表面积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
学习新知
例1. 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(x取3.14)
典型例题
解:一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例2.如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?
解:花盆外壁的表面积:
答:涂100个这样的花盆约需要1000毫升油漆.
涂100个花盆需油漆:
(毫升)
典型例题
例3 圆柱的底面直径与高都等于球的直径.
(1) 求球的体积与圆柱体积之比;
(2) 证明球的表面积等于圆柱的侧面积.
典型例题
(1)解:设球的半径为R,则圆柱的底面半径为R,高为2R.
第2问我们同学自己完成
一个正方体的顶点都在球面上,
它的棱长是4 cm,求这个球的体积.
巩固练习
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
探究 若正方体的棱长为a,则
a
练习:长方体的共顶点的三个侧面积分别为 ,则它的外接球的表面积为_____.
尝试探究
1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
2 . 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图的圆心角为________度
180
巩固练习
3、有一个圆柱形的木块,AD为上底面的一条弦,沿母线AB刨开得矩形ABCD,且AD=24, AB=25,若AD优弧为底面周长的三分之二,
求:1、底面的半径。
2、求圆柱形木块的表面积。
巩固练习
1. 将若干毫升水倒入底面半径为2cm的
圆柱形容器中,量得水面高度为6cm;
若将这些水倒入轴截面是正三角形的
倒圆锥形容器中,求水面的高度.
2. 已知圆锥的侧面积是底面积的2倍,
它的轴截面的面积为4,求圆锥的体积.
3. 仓库一角有谷一堆,呈 圆锥形,
量得底面弧长2.8m,母线长2.2m,
这堆谷多重?
巩固练习
4:用一张面积为900平方厘米的正方形硬纸片围成一个圆柱的侧面,求这个圆柱的底面的直径。
5.一个矩形ABCD的边AB=5cm, AD=8cm,分别以直线AB,AD为轴旋转一周得到的两个不同的圆柱,哪个表面积大?
巩固练习
4.若两球体积之比是1:2,则其表面积之比是______.
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
1.若球的表面积变为原来的2倍,则半径变为原来的___倍.
巩固练习
8.3.2 圆柱圆锥圆台球表面积和体积
(1)矩形面积公式: __________。
(2)圆面积公式: _________。
(3)圆周长公式: _________。
(4)扇形面积公式: _ _________。
复习引入
多面体的表面积
就是围成多面体各个面的面积之和
棱柱的体积
棱锥的体积
棱台的体积
思考
如何根据圆柱,圆锥的几何结构特征,求它们的表面积
与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。
利用圆柱、圆锥、圆台的展开图,可以得到它们的表面积公式
新课引入
圆柱的侧面展开图是矩形
O
圆柱
圆柱、圆锥、圆台的表面积
学习新知
r是底面半径,l是母线长
r是底面半径,l是母线长
圆锥的侧面展开图是扇形
O
侧
=
圆锥
学习新知
r是底面半径,
l是母线长
O
O’
圆台的侧面展开图是扇环
圆台
侧
学习新知
r和 分别是上、下底面半径,l是母线长
圆台
圆柱
圆锥
空间问题“平面”化
圆柱、圆锥、圆台
所用的数学思想:
课堂小结
r是底面半径,l是母线长
r是底面半径,l是母线长
r和 分别是上、下底面半径,l是母线长
圆柱的体积:
圆锥的体积:
体积:几何体所占空间的大小
复习回顾
V棱柱=Sh.
棱柱的体积:
棱锥的体积:
棱台的体积:
圆台的体积:
关于体积有如下几个原理:
(1)相同的几何体的体积相等;
(2)一个几何体的体积等于它的各部分体积之和; (3)等底面积等高的两个同类几何体的体积相等; (4)体积相等的两个几何体叫做等积体.
学习新知
柱体、锥体、台体的体积
锥体
台体
柱体
柱体、锥体、
台体的体积
知识总结
球的表面积公式
半径是R的球的表面积是
S=4 R2
小学,,我们学习了圆的面积公式,你还记得是如何求得的吗
类比这种方法你能由球的表面积公式推导出球的体积公式
学习新知
第一步:分割
O
球面被分割成n个网格,
表面积分别为:
则球的表面积:
则球的体积为:
设“小锥体”的体积为:
O
球的体积公式
学习新知
O
第二步:求近似和
O
由第一步得:
学习新知
第三步:转化为球的体积
如果网格分的越细,则:
①
由①② 得:
②
球的表面积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
学习新知
例1. 如图,某种浮标由两个半球和一个圆柱黏合而成,半球的直径是0.3m,圆柱高0.6m.如果在浮标表面涂一层防水漆,每平方米需要0.5kg涂料,那么给1000个这样的浮标涂防水漆需要多少涂料?(x取3.14)
典型例题
解:一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.8478(m2),
所以给1000个这样的浮标涂防水漆约需涂料
0.8478×0.5×1000=423.9(kg).
例2.如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?
解:花盆外壁的表面积:
答:涂100个这样的花盆约需要1000毫升油漆.
涂100个花盆需油漆:
(毫升)
典型例题
例3 圆柱的底面直径与高都等于球的直径.
(1) 求球的体积与圆柱体积之比;
(2) 证明球的表面积等于圆柱的侧面积.
典型例题
(1)解:设球的半径为R,则圆柱的底面半径为R,高为2R.
第2问我们同学自己完成
一个正方体的顶点都在球面上,
它的棱长是4 cm,求这个球的体积.
巩固练习
⑴正方体的内切球直径=
⑵正方体的外接球直径=
⑶与正方体所有棱相切的球直径=
探究 若正方体的棱长为a,则
a
练习:长方体的共顶点的三个侧面积分别为 ,则它的外接球的表面积为_____.
尝试探究
1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
2 . 已知圆锥的全面积是底面积的3倍,那么这个
圆锥的侧面积展开图的圆心角为________度
180
巩固练习
3、有一个圆柱形的木块,AD为上底面的一条弦,沿母线AB刨开得矩形ABCD,且AD=24, AB=25,若AD优弧为底面周长的三分之二,
求:1、底面的半径。
2、求圆柱形木块的表面积。
巩固练习
1. 将若干毫升水倒入底面半径为2cm的
圆柱形容器中,量得水面高度为6cm;
若将这些水倒入轴截面是正三角形的
倒圆锥形容器中,求水面的高度.
2. 已知圆锥的侧面积是底面积的2倍,
它的轴截面的面积为4,求圆锥的体积.
3. 仓库一角有谷一堆,呈 圆锥形,
量得底面弧长2.8m,母线长2.2m,
这堆谷多重?
巩固练习
4:用一张面积为900平方厘米的正方形硬纸片围成一个圆柱的侧面,求这个圆柱的底面的直径。
5.一个矩形ABCD的边AB=5cm, AD=8cm,分别以直线AB,AD为轴旋转一周得到的两个不同的圆柱,哪个表面积大?
巩固练习
4.若两球体积之比是1:2,则其表面积之比是______.
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
1.若球的表面积变为原来的2倍,则半径变为原来的___倍.
巩固练习
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
