10.1随机事件与概率 同步练习(Word版含解析)
文档属性
| 名称 | 10.1随机事件与概率 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 686.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 03:28:15 | ||
图片预览




文档简介
必修第二册 10.1 随机事件与概率 同步练习
一、单选题
1.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是
A. B. C. D.
2.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
3.“接天莲叶无穷碧,映日荷花别样红”,正值欣赏荷花好时节,家住重庆主城的甲、乙、丙、丁四户家庭都准备从“铜梁爱莲湖、永川十里荷香、大足雅美佳湿地”三个荷花景区选择一个欣赏荷花,则在三个荷花区都有家庭选择的条件下,家庭甲选择“永川十里荷香”的概率为( )
A. B. C. D.
4.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.某天,齐王与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,则田忌获胜概率为( ).
A. B. C. D.
5.已知正六边形的边长为1,在这6个顶点中任意取2个不同的顶点,得到线段,则的概率为( )
A. B. C. D.
6.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为( ).
A. B. C. D.
7.某中学举行党史学习教育知识竞赛,甲队有、、、、、共名选手其中名男生名女生,按比赛规则,比赛时现场从中随机抽出名选手答题,则至少有名女同学被选中的概率是( )
A. B. C. D.
8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
9.下列叙述正确的是( )
A.互斥事件一定不是对立事件,但是对立事件一定是互斥事件
B.若事件发生的概率为,则
C.频率是稳定的,概率是随机的
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性小
10.下列事件:
①任取三条线段,这三条线段恰好组成直角三角形;
②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;
③实数a,b都不为0,但;
④明年12月28日的最高气温高于今年12月28日的最高气温.
其中为随机事件的是( )
A.①②③ B.①③④ C.①②④ D.②③④
11.甲、乙二人玩猜数字游戏,先由甲任想一数字,记为a,再由乙猜甲刚才想的数字,把乙猜出的数字记为b,且,若,则称甲乙“心有灵犀”.现任意找两个人玩这个游戏,则他们“心有灵犀”的概率为( )
A. B. C. D.
12.饕餮纹是青铜器上常见的花纹之一,最早见于长江中下游地区的良渚文化陶器和玉器上,盛行于商代至西周早期.将青铜器中的饕餮纹的一部分画到方格纸上,如图所示,每个小方格的边长为一个单位长度,有一点从点出发,每次向右或向下跳一个单位长度,且向右或向下跳是等可能的,那么点经过3次跳动后恰好是沿着饕餮纹的路线到达点的概率为( )
A. B. C. D.
二、填空题
13.在10件产品中有8件一级品,2件二级品,从中任取3件,若记“3件都是一级品”为事件A,则A的对立事件是___________.
14.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
15.从0,2,4,6,8这5个数中任取两个数作差,则差值恰好为2的概率是______.
16.从集合中随机选取一个数记为,从集合中随机选取一个数记为,则一次函数的图象不经过第二象限的概率为______.
17.若随机事件、互斥,、发生的概率均不等于0,且分别为,,则实数a的取值范围为_____.
三、解答题
18.有2个人在一座11层大楼的底层进入电梯,设他们中的每一个人自第二层开始在每一层离开是等可能的,求2个人在不同层离开的概率.
19.设A,B,C表示三个随机事件,试将下列事件用A,B,C表示出来.
(1)三个事件都发生;
(2)三个事件至少有一个发生;
(3)A发生,B,C不发生;
(4)A,B都发生,C不发生;
(5)A,B至少有一个发生,C不发生;
(6)A,B,C中恰好有两个发生.
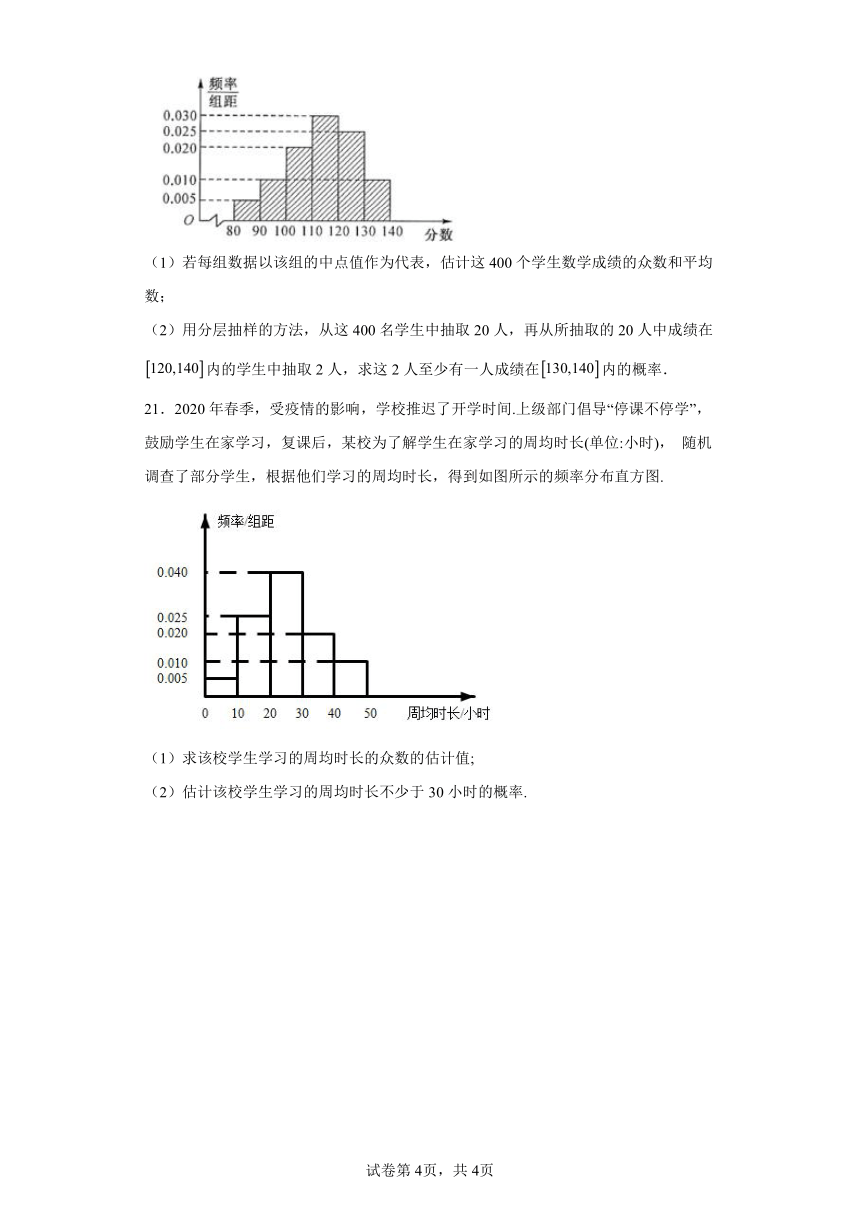
20.某校2020届高三数学教师为分析本校2019年高考文科数学成绩,从该校文科生中随机抽取400名学生的数学成绩进行统计,将他们的成绩分成六段,,,,,后得到如图所示的频率分布直方图.
(1)若每组数据以该组的中点值作为代表,估计这400个学生数学成绩的众数和平均数;
(2)用分层抽样的方法,从这400名学生中抽取20人,再从所抽取的20人中成绩在内的学生中抽取2人,求这2人至少有一人成绩在内的概率.
21.2020年春季,受疫情的影响,学校推迟了开学时间.上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时), 随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.
(1)求该校学生学习的周均时长的众数的估计值;
(2)估计该校学生学习的周均时长不少于30小时的概率.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.D
由随机事件、互斥,、发生的概率均不等于0,知,由此能求出实数的取值范围.
【详解】
随机事件、互斥,、发生的概率均不等于0,
且,,
,即,
解得,即.
故选:D.
本题考查互斥事件的概率的应用,属于基础题.解题时要认真审题,仔细解答.
2.C
由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】
解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
3.B
分别算出基本事件数,进而计算相应概率即可.
【详解】
解:在三个荷花区都有家庭选择的条件下,基本事件总数为,
家庭甲选择“永川十里荷香”包含的基本事件个数为.
所以家庭甲选择“永川十里荷香”的概率.
故选:B.
本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,分析问题能力,属于基础题.
4.B
设齐王的三匹马分别为,田忌的三匹马分别为,列举所有比赛的情况,利用古典概型的概率公式计算即可得出结果.
【详解】
设齐王的三匹马分别为,田忌的三匹马分别为,所有比赛的情况::
、、,齐王获胜三局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,田忌获胜两局;
、、,齐王获胜两局,共6种情况,则田忌胜1种情况,故概率为
故选:B
本题考查了古典概型的概率计算问题,考查了理解辨析和数学运算能力,属于中档题目.
5.C
先分析,然后列举基本事件,根据古典概型的概率公式直接求得.
【详解】
由已知得,,,在这6个顶点中任意取2个不同的顶点,,得到以下15条线段:,,,,,,,,,,,,,,,其中满足的有以下6条线段:,,,,,,根据古典概型的计算公式得,的概率为.
故选C.
古典概型的概率计算中列举基本事件的方法:
(1)枚举法;(2)列表法;(3)坐标法;(4)树状图法.
6.C
根据题意,设齐王的上,中,下三个等次的马分别为a, b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,用列举法列举齐王与田忌赛马的情况,进而可得田忌胜出的情况数目,进而由等可能事件的概率计算可得答案.
【详解】
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
7.D
现场选名选手,共种情况,设,,,四位同学为男同学则没有女同学被选中的情况,共有6种,利用对立事件进行求解,即可得到答案;
【详解】
现场选名选手,基本事件有:,,,,,,,,,,,,,,共种情况,不妨设,,,四位同学为男同学则没有女同学被选中的情况是:,,,,,共种, 则至少有一名女同学被选中的概率为.
故选:.
8.C
【详解】
分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法: (1)列举法. (2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法. (3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法:适用于限制条件较多且元素数目较多的题目.
9.B
由互斥事件及对立事件的关系,频率与概率的关系及随机事件的概率逐一判断即可得解.
【详解】
解:对于A,互斥事件不一定是对立事件,但是对立事件一定是互斥事件,即A错误;
对于B,事件发生的概率为,则,即B正确;
对于C,概率是稳定的,频率是随机的,即C错误;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性都为,即D错误,
即叙述正确的是选项B,
故选:B.
本题考查了互斥事件及对立事件的关系,重点考查了频率与概率的关系及随机事件的概率,属基础题.
10.C
根据随机事件概念逐一判断,即可选择.
【详解】
任取三条线段,这三条线段不一定能组成直角三角形,所以①为随机事件;
从一个三角形的三个顶点各任画一条射线,这三条射线不一定交于一点,所以②为随机事件;
因为当实数a,b都不为0时,所以③为不可能事件;
明年12月28日的最高气温可能高于今年12月28日的最高气温,所以④为随机事件;
故选C.
本题考查随机事件概念,考查基本分析判断能力,属基础题.
11.B
利用列举法根据古典概型公式计算即可.
【详解】
B两人分别从1,2,3,4四个数中任取一个,共有16个样本点,为:(1,1),(1,2),(1,3),(1,4), (2,1),(2,2),(2,3) ,(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2) (4,3),(4,4),这16个样本点发生的可能性是相等的.
其中满足的样本点有(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),共10个,故他们“心有灵犀”的概率为.
故选:B
12.B
利用古典概型的概率求解.
【详解】
解:点从点出发,每次向右或向下跳一个单位长度,跳3次,
则样本空间{(右,右,右),(右,右,下),(右,下,右),(下,右,右),(右,下,下),(下,右,下),(下,下,右),(下,下,下)},
记“3次跳动后,恰好是沿着饕餮纹的路线到达点B”为事件,则{(下,下,右)},由古典概型的概率公式可知.
故选:B.
13.3件至多有2件一级品
根据对立事件的定义即可得到答案.
【详解】
“3件都是一级品”为事件A,则A的对立事件为“3件不都是一级品”,
即为“3件至多有2件一级品”.
故答案为:3件至多有2件一级品.
14.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
15.;
运用列举法列出在5个数取2个数的所的情况,再找出差值为2的两个数,由古典概率公式可得答案.
【详解】
在0,2,4,6,8这5个数中任取两个数作差有以下情况:
,
共有20种情况,
其中差值恰好为2的是,有4种情况,
所以两个数差值恰好为2的概率是,
故答案为:.
本题考查用列举法求古典概率的问题,属于基础题.
16.
列举出试验发生包含的事件的所有可能的结果及满足条件直线不经过第二象限的事件,根据古典概型概率公式得到结果.
【详解】
依题意和的所有可能的取法有,,,,,,,,,共9种,因为题中,均不为0,所以当一次函数的图象不经过第二象限时,应有,,满足条件的取法有,,,,共4种,故所求概率为.
故答案为:.
17.
根据已知条件和随机事件的概率范围及互斥事件的性质,列出不等式组,即可求出实数a的取值范围.
【详解】
因为随机事件、互斥,、发生的概率均不等于0,所以有:
,即,解得,
故答案为:
18.
由题可得两个人离开的所有可能结果及两人同层离开的结果,再利用古典概型概率公式及对立事件的概率公式计算可得.
【详解】
每个人自第二层开始在每一层离开电梯的可能结果都是10种,两个人共有种可能,
其中2人在相同楼层离开的结果有10种,故2个人在相同楼层离开的概率为,
所以2个人在不同层离开的概率为.
19.(1);(2);(3);(4);(5);(6)
由互斥事件和对立事件的定义、事件的间的关系求解即可
【详解】
解:(1)三个事件都发生表示为;
(2)三个事件至少有一个发生表示为;
(3)A发生,B,C不发生表示为;
(4)A,B都发生,C不发生表示为;
(5)A,B至少有一个发生,C不发生表示为;
(6)A,B,C中恰好有两个发生表示为
20.(1)众数的估计值为115,平均数的估计值为;(2).
(1)根据频率分布直方图,结合众数和平均数的计算,即可容易求得结果;
(2)利用分层抽样求得在各个区间抽取的人数,列举所有抽取的可能,找出满足题意的可能,用古典概型的概率计算公式,即可求得结果.
【详解】
(1)众数的估计值为最高矩形对应的成绩区间的中点,即众数的估计值为115,
平均数的估计值为
.
(2)由频率分布直方图可得,成绩在内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
按分层抽样方法,抽取20人,则成绩在内的抽1人,
在内的抽2人,在内的抽4人,
在内的抽6人,在内的抽5人,
在内的抽2人.
记成绩在内的5人分别为,,,,,
成绩在内的2人分别为,,
则从成绩在内的学生中任取2人的基本事件有
,,,,,,
,,,,,,
,,,,,,
,,,共21种,
其中成绩在中至少有一人的基本事件有
,,,,,,
,,,,,共11种,
所以2人中至少有一人成绩在内的概率.
本题考查由频率分布直方图计算众数和平均数,以及古典概型的概率求解,涉及分层抽样,属综合基础题.
21.(1)25小时;(2)0.3.
(1)根据直方图,频率最大的区间中点横坐标为众数即可求众数;(2)由学习的周均时长不少于30小时的区间有、,它们的频率之和,即为该校学生学习的周均时长不少于30小时的概率.
【详解】
(1)根据直方图知:频率最大的区间中点横坐标即为众数,
∴由频率最大区间为,则众数为;
(2)由图知:不少于30小时的区间有、,
∴该校学生学习的周均时长不少于30小时的概率.
本题考查了根据直方图求众数、概率,应用了众数的概念、频率法求概率,属于简单题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若随机事件,互斥,,发生的概率均不等于0,且,,则实数的取值范围是
A. B. C. D.
2.掷一枚骰子的试验中,出现各点的概率均为,事件A表示“小于5的偶数点出现”,事件B表示“小于5的点数出现”,则一次试验中,事件A+(表示事件B的对立事件)发生的概率为( )
A. B. C. D.
3.“接天莲叶无穷碧,映日荷花别样红”,正值欣赏荷花好时节,家住重庆主城的甲、乙、丙、丁四户家庭都准备从“铜梁爱莲湖、永川十里荷香、大足雅美佳湿地”三个荷花景区选择一个欣赏荷花,则在三个荷花区都有家庭选择的条件下,家庭甲选择“永川十里荷香”的概率为( )
A. B. C. D.
4.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.某天,齐王与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,则田忌获胜概率为( ).
A. B. C. D.
5.已知正六边形的边长为1,在这6个顶点中任意取2个不同的顶点,得到线段,则的概率为( )
A. B. C. D.
6.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为( ).
A. B. C. D.
7.某中学举行党史学习教育知识竞赛,甲队有、、、、、共名选手其中名男生名女生,按比赛规则,比赛时现场从中随机抽出名选手答题,则至少有名女同学被选中的概率是( )
A. B. C. D.
8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
9.下列叙述正确的是( )
A.互斥事件一定不是对立事件,但是对立事件一定是互斥事件
B.若事件发生的概率为,则
C.频率是稳定的,概率是随机的
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性小
10.下列事件:
①任取三条线段,这三条线段恰好组成直角三角形;
②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;
③实数a,b都不为0,但;
④明年12月28日的最高气温高于今年12月28日的最高气温.
其中为随机事件的是( )
A.①②③ B.①③④ C.①②④ D.②③④
11.甲、乙二人玩猜数字游戏,先由甲任想一数字,记为a,再由乙猜甲刚才想的数字,把乙猜出的数字记为b,且,若,则称甲乙“心有灵犀”.现任意找两个人玩这个游戏,则他们“心有灵犀”的概率为( )
A. B. C. D.
12.饕餮纹是青铜器上常见的花纹之一,最早见于长江中下游地区的良渚文化陶器和玉器上,盛行于商代至西周早期.将青铜器中的饕餮纹的一部分画到方格纸上,如图所示,每个小方格的边长为一个单位长度,有一点从点出发,每次向右或向下跳一个单位长度,且向右或向下跳是等可能的,那么点经过3次跳动后恰好是沿着饕餮纹的路线到达点的概率为( )
A. B. C. D.
二、填空题
13.在10件产品中有8件一级品,2件二级品,从中任取3件,若记“3件都是一级品”为事件A,则A的对立事件是___________.
14.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
15.从0,2,4,6,8这5个数中任取两个数作差,则差值恰好为2的概率是______.
16.从集合中随机选取一个数记为,从集合中随机选取一个数记为,则一次函数的图象不经过第二象限的概率为______.
17.若随机事件、互斥,、发生的概率均不等于0,且分别为,,则实数a的取值范围为_____.
三、解答题
18.有2个人在一座11层大楼的底层进入电梯,设他们中的每一个人自第二层开始在每一层离开是等可能的,求2个人在不同层离开的概率.
19.设A,B,C表示三个随机事件,试将下列事件用A,B,C表示出来.
(1)三个事件都发生;
(2)三个事件至少有一个发生;
(3)A发生,B,C不发生;
(4)A,B都发生,C不发生;
(5)A,B至少有一个发生,C不发生;
(6)A,B,C中恰好有两个发生.
20.某校2020届高三数学教师为分析本校2019年高考文科数学成绩,从该校文科生中随机抽取400名学生的数学成绩进行统计,将他们的成绩分成六段,,,,,后得到如图所示的频率分布直方图.
(1)若每组数据以该组的中点值作为代表,估计这400个学生数学成绩的众数和平均数;
(2)用分层抽样的方法,从这400名学生中抽取20人,再从所抽取的20人中成绩在内的学生中抽取2人,求这2人至少有一人成绩在内的概率.
21.2020年春季,受疫情的影响,学校推迟了开学时间.上级部门倡导“停课不停学”,鼓励学生在家学习,复课后,某校为了解学生在家学习的周均时长(单位:小时), 随机调查了部分学生,根据他们学习的周均时长,得到如图所示的频率分布直方图.
(1)求该校学生学习的周均时长的众数的估计值;
(2)估计该校学生学习的周均时长不少于30小时的概率.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.D
由随机事件、互斥,、发生的概率均不等于0,知,由此能求出实数的取值范围.
【详解】
随机事件、互斥,、发生的概率均不等于0,
且,,
,即,
解得,即.
故选:D.
本题考查互斥事件的概率的应用,属于基础题.解题时要认真审题,仔细解答.
2.C
由题意知试验发生包含的所有事件共有6种,事件和事件是互斥事件,看出事件和事件包含的基本事件数,根据互斥事件和古典概型概率公式得到结果.
【详解】
解:事件表示“小于5的点数出现”,
的对立事件是“大于或等于5的点数出现”,
表示事件是出现点数为5和6.
事件表示“小于5的偶数点出现”,
它包含的事件是出现点数为2和4,
,
.
故选:C.
3.B
分别算出基本事件数,进而计算相应概率即可.
【详解】
解:在三个荷花区都有家庭选择的条件下,基本事件总数为,
家庭甲选择“永川十里荷香”包含的基本事件个数为.
所以家庭甲选择“永川十里荷香”的概率.
故选:B.
本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,分析问题能力,属于基础题.
4.B
设齐王的三匹马分别为,田忌的三匹马分别为,列举所有比赛的情况,利用古典概型的概率公式计算即可得出结果.
【详解】
设齐王的三匹马分别为,田忌的三匹马分别为,所有比赛的情况::
、、,齐王获胜三局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,齐王获胜两局;
、、,田忌获胜两局;
、、,齐王获胜两局,共6种情况,则田忌胜1种情况,故概率为
故选:B
本题考查了古典概型的概率计算问题,考查了理解辨析和数学运算能力,属于中档题目.
5.C
先分析,然后列举基本事件,根据古典概型的概率公式直接求得.
【详解】
由已知得,,,在这6个顶点中任意取2个不同的顶点,,得到以下15条线段:,,,,,,,,,,,,,,,其中满足的有以下6条线段:,,,,,,根据古典概型的计算公式得,的概率为.
故选C.
古典概型的概率计算中列举基本事件的方法:
(1)枚举法;(2)列表法;(3)坐标法;(4)树状图法.
6.C
根据题意,设齐王的上,中,下三个等次的马分别为a, b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,用列举法列举齐王与田忌赛马的情况,进而可得田忌胜出的情况数目,进而由等可能事件的概率计算可得答案.
【详解】
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
7.D
现场选名选手,共种情况,设,,,四位同学为男同学则没有女同学被选中的情况,共有6种,利用对立事件进行求解,即可得到答案;
【详解】
现场选名选手,基本事件有:,,,,,,,,,,,,,,共种情况,不妨设,,,四位同学为男同学则没有女同学被选中的情况是:,,,,,共种, 则至少有一名女同学被选中的概率为.
故选:.
8.C
【详解】
分析:先确定不超过30的素数,再确定两个不同的数的和等于30的取法,最后根据古典概型概率公式求概率.
详解:不超过30的素数有2,3,5,7,11,13,17,19,23,29,共10个,随机选取两个不同的数,共有种方法,因为,所以随机选取两个不同的数,其和等于30的有3种方法,故概率为,选C.
点睛:古典概型中基本事件数的探求方法: (1)列举法. (2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法. (3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化. (4)排列组合法:适用于限制条件较多且元素数目较多的题目.
9.B
由互斥事件及对立事件的关系,频率与概率的关系及随机事件的概率逐一判断即可得解.
【详解】
解:对于A,互斥事件不一定是对立事件,但是对立事件一定是互斥事件,即A错误;
对于B,事件发生的概率为,则,即B正确;
对于C,概率是稳定的,频率是随机的,即C错误;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙比甲抽到有奖奖券的可能性都为,即D错误,
即叙述正确的是选项B,
故选:B.
本题考查了互斥事件及对立事件的关系,重点考查了频率与概率的关系及随机事件的概率,属基础题.
10.C
根据随机事件概念逐一判断,即可选择.
【详解】
任取三条线段,这三条线段不一定能组成直角三角形,所以①为随机事件;
从一个三角形的三个顶点各任画一条射线,这三条射线不一定交于一点,所以②为随机事件;
因为当实数a,b都不为0时,所以③为不可能事件;
明年12月28日的最高气温可能高于今年12月28日的最高气温,所以④为随机事件;
故选C.
本题考查随机事件概念,考查基本分析判断能力,属基础题.
11.B
利用列举法根据古典概型公式计算即可.
【详解】
B两人分别从1,2,3,4四个数中任取一个,共有16个样本点,为:(1,1),(1,2),(1,3),(1,4), (2,1),(2,2),(2,3) ,(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2) (4,3),(4,4),这16个样本点发生的可能性是相等的.
其中满足的样本点有(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4),共10个,故他们“心有灵犀”的概率为.
故选:B
12.B
利用古典概型的概率求解.
【详解】
解:点从点出发,每次向右或向下跳一个单位长度,跳3次,
则样本空间{(右,右,右),(右,右,下),(右,下,右),(下,右,右),(右,下,下),(下,右,下),(下,下,右),(下,下,下)},
记“3次跳动后,恰好是沿着饕餮纹的路线到达点B”为事件,则{(下,下,右)},由古典概型的概率公式可知.
故选:B.
13.3件至多有2件一级品
根据对立事件的定义即可得到答案.
【详解】
“3件都是一级品”为事件A,则A的对立事件为“3件不都是一级品”,
即为“3件至多有2件一级品”.
故答案为:3件至多有2件一级品.
14.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
15.;
运用列举法列出在5个数取2个数的所的情况,再找出差值为2的两个数,由古典概率公式可得答案.
【详解】
在0,2,4,6,8这5个数中任取两个数作差有以下情况:
,
共有20种情况,
其中差值恰好为2的是,有4种情况,
所以两个数差值恰好为2的概率是,
故答案为:.
本题考查用列举法求古典概率的问题,属于基础题.
16.
列举出试验发生包含的事件的所有可能的结果及满足条件直线不经过第二象限的事件,根据古典概型概率公式得到结果.
【详解】
依题意和的所有可能的取法有,,,,,,,,,共9种,因为题中,均不为0,所以当一次函数的图象不经过第二象限时,应有,,满足条件的取法有,,,,共4种,故所求概率为.
故答案为:.
17.
根据已知条件和随机事件的概率范围及互斥事件的性质,列出不等式组,即可求出实数a的取值范围.
【详解】
因为随机事件、互斥,、发生的概率均不等于0,所以有:
,即,解得,
故答案为:
18.
由题可得两个人离开的所有可能结果及两人同层离开的结果,再利用古典概型概率公式及对立事件的概率公式计算可得.
【详解】
每个人自第二层开始在每一层离开电梯的可能结果都是10种,两个人共有种可能,
其中2人在相同楼层离开的结果有10种,故2个人在相同楼层离开的概率为,
所以2个人在不同层离开的概率为.
19.(1);(2);(3);(4);(5);(6)
由互斥事件和对立事件的定义、事件的间的关系求解即可
【详解】
解:(1)三个事件都发生表示为;
(2)三个事件至少有一个发生表示为;
(3)A发生,B,C不发生表示为;
(4)A,B都发生,C不发生表示为;
(5)A,B至少有一个发生,C不发生表示为;
(6)A,B,C中恰好有两个发生表示为
20.(1)众数的估计值为115,平均数的估计值为;(2).
(1)根据频率分布直方图,结合众数和平均数的计算,即可容易求得结果;
(2)利用分层抽样求得在各个区间抽取的人数,列举所有抽取的可能,找出满足题意的可能,用古典概型的概率计算公式,即可求得结果.
【详解】
(1)众数的估计值为最高矩形对应的成绩区间的中点,即众数的估计值为115,
平均数的估计值为
.
(2)由频率分布直方图可得,成绩在内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
内的人数为(人),
按分层抽样方法,抽取20人,则成绩在内的抽1人,
在内的抽2人,在内的抽4人,
在内的抽6人,在内的抽5人,
在内的抽2人.
记成绩在内的5人分别为,,,,,
成绩在内的2人分别为,,
则从成绩在内的学生中任取2人的基本事件有
,,,,,,
,,,,,,
,,,,,,
,,,共21种,
其中成绩在中至少有一人的基本事件有
,,,,,,
,,,,,共11种,
所以2人中至少有一人成绩在内的概率.
本题考查由频率分布直方图计算众数和平均数,以及古典概型的概率求解,涉及分层抽样,属综合基础题.
21.(1)25小时;(2)0.3.
(1)根据直方图,频率最大的区间中点横坐标为众数即可求众数;(2)由学习的周均时长不少于30小时的区间有、,它们的频率之和,即为该校学生学习的周均时长不少于30小时的概率.
【详解】
(1)根据直方图知:频率最大的区间中点横坐标即为众数,
∴由频率最大区间为,则众数为;
(2)由图知:不少于30小时的区间有、,
∴该校学生学习的周均时长不少于30小时的概率.
本题考查了根据直方图求众数、概率,应用了众数的概念、频率法求概率,属于简单题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
