1.1.1空间向量及其线性运算 课件(共20张PPT)
文档属性
| 名称 | 1.1.1空间向量及其线性运算 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 458.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
【课标要求】
空间向量及其线性运算
空间向量及其运算
掌握空间向量相关的概念,几何表示法、字母表示法.
掌握空间向量的加减运算及运算律.
借助图形理解空间向量加减运算及其运算律的意义.
1.
2.
3.
空间向量的线性运算及其性质,空间向量共线的充要条件.(重点)
向量及其运算由平面向空间的推广.(难点)
【核心扫描】
1.
2.
空间向量的概念
在空间中,具有_____和_____的量叫做空间向量,向量的大小叫向量的_________ .
空间向量的加减法
(1)加减法定义
自学导引
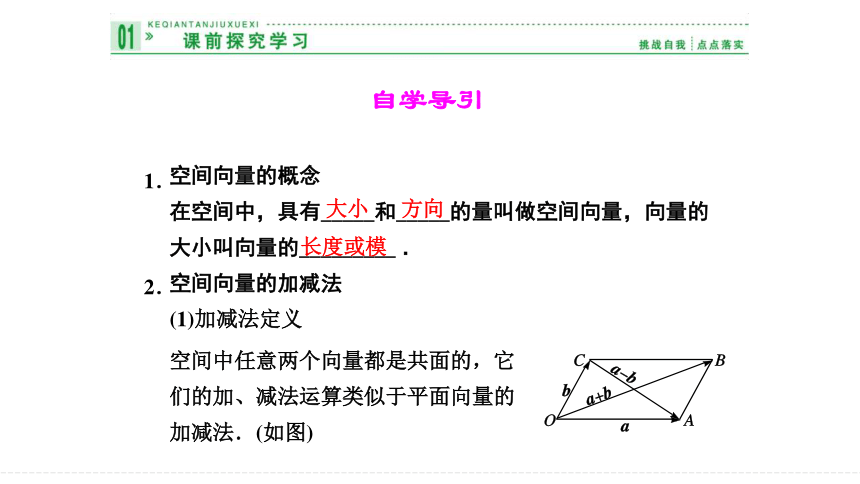
空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如图)
1.
2.
大小
方向
长度或模
(2)运算律
交换律:a+b=b+a;
结合律:(a+b)+c=a+(b+c).
空间向量的数乘运算
(1)定义
实数λ与空间向量a的乘积λa仍是一个向量,称为向量的数乘运算.当λ>0时,λa与a方向_____;当λ<0时,λa与a方向_____ ;当λ=0时,λa=___.λa的长度是a的长度为|λ|倍.如图所示.
a+b
a-b
3.
相同
相反
0
(2)运算律
分配律:λ(a+b)=λa+λb;
结合律:λ(μa)=(λμ)a.
共线定理
(1)共线向量的定义
与平面向量一样,如果表示空间向量的有向线段所在的___________________,则这些向量叫做_________或平行向量,记作a∥b.
4.
直线互相平行或重合
共线向量
(2)充要条件:对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ使______.
想一想:空间向量与平面向量有何关系?
提示 空间向量是平面向量的推广,空间向量线性运算与平面向量的线性运算相同.
b=λa
几类特殊向量
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:长度等于1的向量称为单位向量.
(3)相等向量:方向相同且模相等的向量称为相等向量,在空间,同向且等长的有向线段表示同一向量或相等向量.
(4)相反向量:与向量a长度相等而方向相反的向量,称为a的相反向量,记为-a.
名师点睛
1.
空间向量与平面向量的加减运算的联系
(1)空间任意两个向量都可以平移到同一个平面内,成为同一个平面内的两个向量,因而空间任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加、减法运算.
(2)向量加法的平行四边形法则在空间仍成立,在运用三角形法则或平行四边形法则求两个向量的和或差向量时要注意起点和终点;a-b表示从向量b的终点指向向量a的终点的向量.
2.
题型一 空间向量的概念
(2)将空间中所有的单位向量移到同一个点为起点,则它们的终点构成一个圆;
(3)空间向量就是空间中的一条有向线段;
(4)不相等的两个空间向量的模必不相等.
[思路探索] 对照空间向量的基本概念逐一判断.
【例1】
(2)假命题.将空间中所有的单位向量移到同一个点为起点时,它们的终点将构成一个球面,而不是一个圆.
(3)假命题.有向线段只是空间向量的一种表示形式,但不能把二者完全等同起来.
(4)假命题.不相等的两个空间向量的模也可以相等,只要它们的方向不相同即可.
规律方法 关键在于正确理解空间向量的有关概念.
解析 当两个空间向量的起点相同,终点也相同时,这两个向量必相等;但两个向量相等,却不一定有起点相同、终点相同,故①错;根据向量相等的定义,要保证两向量相等,不仅模要相等,而且方向还要相同,但②中向量a与
【变式1】
答案 3
[思路探索] 在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后像平面向量求和那样,运用向量运算定律、平行四边形法则、三角形法则及多边形法则来求解.
题型二 空间向量的线性运算
【例2】
规律方法 化简向量表达式主要是利用平行四边形法则或三角形法则,遇到减法时既可转化成加法,也可按减法法则进行运算.加减法之间可以转化.表达式中各向量的系数相等时,根据数乘分配律,可以把相同的系数提到括号外面.
【变式2】
审题指导 本题综合考查空间向量共线定理的应用.
题型三 空间向量的共线问题
【例3】
【题后反思】 灵活应用共线向量定理,正确列出比例式.
【变式3】
给出下面命题:
①空间任意两个向量a,b一定是共面的.②a∥b 存在唯一的λ∈R,使b=λa.③若a∥b,则a与b所在直线平行.④如果a∥b,b∥c,那么a∥c.
其中假命题的序号是________.
[错解] ②
0与任意向量是共线向量,a≠0不可丢掉,否则实数λ就不唯一.
误区警示 对空间向量有关概念误解致错
【示例】
[正解] ①空间任意两个向量都是共面的.②中前提是a≠0.③a∥b时,它们所在直线平行或重合.即用共线向量充要条件判定a、b所在直线平行,还需a(或b)上有一点不在b(或a)上.④共线向量不具有传递性,若a∥b,b∥c,则a∥c就不一定成立,由于当b=0时,虽然a∥b,b∥c,但a不一定与c共线.所以假命题的序号为②③④.
在掌握向量加减法的同时,应首先掌握有特殊位置关系的两个向量的和或差,如共线、共起点、共终点等.
【课标要求】
空间向量及其线性运算
空间向量及其运算
掌握空间向量相关的概念,几何表示法、字母表示法.
掌握空间向量的加减运算及运算律.
借助图形理解空间向量加减运算及其运算律的意义.
1.
2.
3.
空间向量的线性运算及其性质,空间向量共线的充要条件.(重点)
向量及其运算由平面向空间的推广.(难点)
【核心扫描】
1.
2.
空间向量的概念
在空间中,具有_____和_____的量叫做空间向量,向量的大小叫向量的_________ .
空间向量的加减法
(1)加减法定义
自学导引
空间中任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加减法.(如图)
1.
2.
大小
方向
长度或模
(2)运算律
交换律:a+b=b+a;
结合律:(a+b)+c=a+(b+c).
空间向量的数乘运算
(1)定义
实数λ与空间向量a的乘积λa仍是一个向量,称为向量的数乘运算.当λ>0时,λa与a方向_____;当λ<0时,λa与a方向_____ ;当λ=0时,λa=___.λa的长度是a的长度为|λ|倍.如图所示.
a+b
a-b
3.
相同
相反
0
(2)运算律
分配律:λ(a+b)=λa+λb;
结合律:λ(μa)=(λμ)a.
共线定理
(1)共线向量的定义
与平面向量一样,如果表示空间向量的有向线段所在的___________________,则这些向量叫做_________或平行向量,记作a∥b.
4.
直线互相平行或重合
共线向量
(2)充要条件:对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ使______.
想一想:空间向量与平面向量有何关系?
提示 空间向量是平面向量的推广,空间向量线性运算与平面向量的线性运算相同.
b=λa
几类特殊向量
(1)零向量:长度为0的向量叫做零向量,记为0.
(2)单位向量:长度等于1的向量称为单位向量.
(3)相等向量:方向相同且模相等的向量称为相等向量,在空间,同向且等长的有向线段表示同一向量或相等向量.
(4)相反向量:与向量a长度相等而方向相反的向量,称为a的相反向量,记为-a.
名师点睛
1.
空间向量与平面向量的加减运算的联系
(1)空间任意两个向量都可以平移到同一个平面内,成为同一个平面内的两个向量,因而空间任意两个向量都是共面的,它们的加、减法运算类似于平面向量的加、减法运算.
(2)向量加法的平行四边形法则在空间仍成立,在运用三角形法则或平行四边形法则求两个向量的和或差向量时要注意起点和终点;a-b表示从向量b的终点指向向量a的终点的向量.
2.
题型一 空间向量的概念
(2)将空间中所有的单位向量移到同一个点为起点,则它们的终点构成一个圆;
(3)空间向量就是空间中的一条有向线段;
(4)不相等的两个空间向量的模必不相等.
[思路探索] 对照空间向量的基本概念逐一判断.
【例1】
(2)假命题.将空间中所有的单位向量移到同一个点为起点时,它们的终点将构成一个球面,而不是一个圆.
(3)假命题.有向线段只是空间向量的一种表示形式,但不能把二者完全等同起来.
(4)假命题.不相等的两个空间向量的模也可以相等,只要它们的方向不相同即可.
规律方法 关键在于正确理解空间向量的有关概念.
解析 当两个空间向量的起点相同,终点也相同时,这两个向量必相等;但两个向量相等,却不一定有起点相同、终点相同,故①错;根据向量相等的定义,要保证两向量相等,不仅模要相等,而且方向还要相同,但②中向量a与
【变式1】
答案 3
[思路探索] 在进行减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在进行加法运算时,首先考虑这两个向量在哪个平面内,然后像平面向量求和那样,运用向量运算定律、平行四边形法则、三角形法则及多边形法则来求解.
题型二 空间向量的线性运算
【例2】
规律方法 化简向量表达式主要是利用平行四边形法则或三角形法则,遇到减法时既可转化成加法,也可按减法法则进行运算.加减法之间可以转化.表达式中各向量的系数相等时,根据数乘分配律,可以把相同的系数提到括号外面.
【变式2】
审题指导 本题综合考查空间向量共线定理的应用.
题型三 空间向量的共线问题
【例3】
【题后反思】 灵活应用共线向量定理,正确列出比例式.
【变式3】
给出下面命题:
①空间任意两个向量a,b一定是共面的.②a∥b 存在唯一的λ∈R,使b=λa.③若a∥b,则a与b所在直线平行.④如果a∥b,b∥c,那么a∥c.
其中假命题的序号是________.
[错解] ②
0与任意向量是共线向量,a≠0不可丢掉,否则实数λ就不唯一.
误区警示 对空间向量有关概念误解致错
【示例】
[正解] ①空间任意两个向量都是共面的.②中前提是a≠0.③a∥b时,它们所在直线平行或重合.即用共线向量充要条件判定a、b所在直线平行,还需a(或b)上有一点不在b(或a)上.④共线向量不具有传递性,若a∥b,b∥c,则a∥c就不一定成立,由于当b=0时,虽然a∥b,b∥c,但a不一定与c共线.所以假命题的序号为②③④.
在掌握向量加减法的同时,应首先掌握有特殊位置关系的两个向量的和或差,如共线、共起点、共终点等.
