1.1空间向量及其运算 课件(共14张PPT)
文档属性
| 名称 | 1.1空间向量及其运算 课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 151.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 09:22:59 | ||
图片预览



文档简介
(共14张PPT)
空间向量及其运算
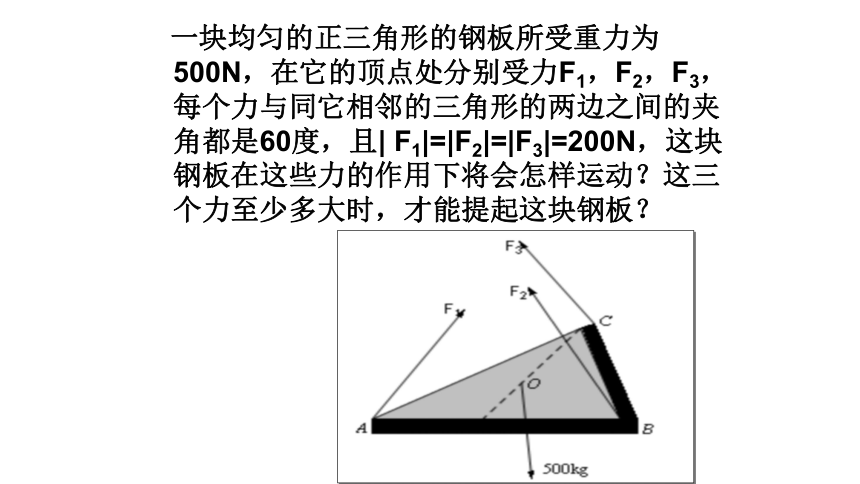
图3.1-1
一块均匀的正三角形的钢板所受重力为500N,在它的顶点处分别受力F1,F2,F3,每个力与同它相邻的三角形的两边之间的夹角都是60度,且| F1|=|F2|=|F3|=200N,这块钢板在这些力的作用下将会怎样运动?这三个力至少多大时,才能提起这块钢板?
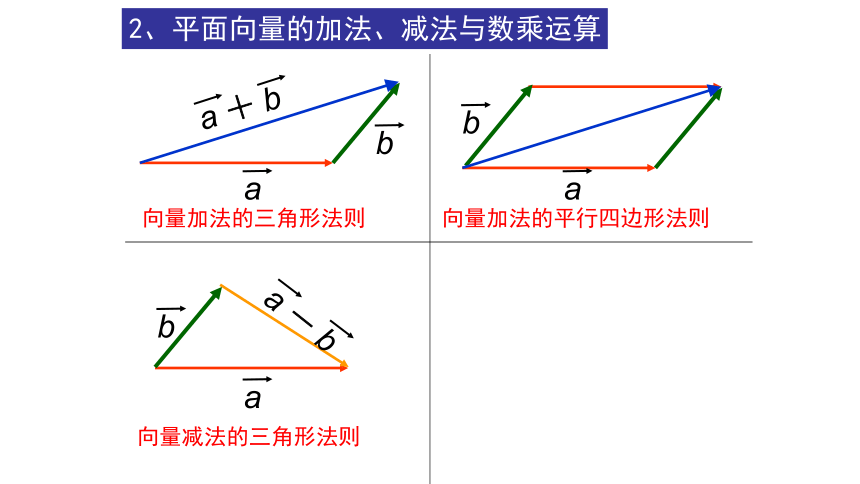
2、平面向量的加法、减法与数乘运算
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
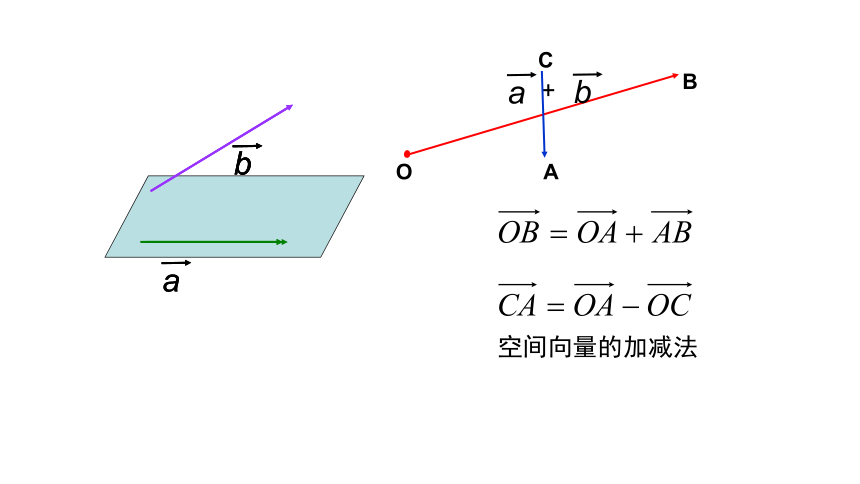
空间向量及其加减运算
空间向量
具有大小和方向的量
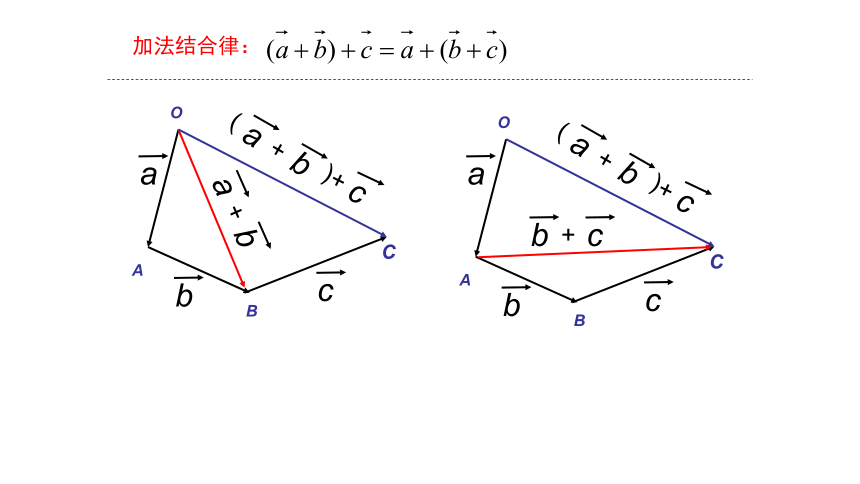
加法交换律
加法结合律
a
b
a
b
a
b
+
O
A
B
b
C
空间向量的加减法
平面向量
概念
加法
减法
数乘
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量及其加减运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
加法交换律
加法结合律:
a
b
c
a
b
+
c
+
(
)
O
A
B
C
a
b
+
a
b
c
a
b
+
c
+
(
)
O
A
B
C
b
c
+
推广:
(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。
a
b
a
b
O
A
B
b
结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。
思考:它们确定的平面是否唯一?
思考:空间任意两个向量是否可能异面?
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)
A
B
C
D
A1
B1
C1
D1
1.课本P92练习1-3
2.如图,在三棱柱
中,M是
并在图中标出化简得到的向量:
的中点,化简下列各式,
(1)
(2)
(3)
3.已知空间四边形
,连结
,设
分别是
化简下列各表达式,并标出化简结果向量:
(1)
(2)
(3)
的中点,
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量
具有大小和方向的量
加法交换律
加法结合律
小结
加法交换律
加法结合律
类比思想 数形结合思想
课本P106习题3.1,
A组 第1题(1)、(2)
空间向量及其运算
图3.1-1
一块均匀的正三角形的钢板所受重力为500N,在它的顶点处分别受力F1,F2,F3,每个力与同它相邻的三角形的两边之间的夹角都是60度,且| F1|=|F2|=|F3|=200N,这块钢板在这些力的作用下将会怎样运动?这三个力至少多大时,才能提起这块钢板?
2、平面向量的加法、减法与数乘运算
向量加法的三角形法则
a
b
向量加法的平行四边形法则
b
a
向量减法的三角形法则
a
b
a -
b
a +
b
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量及其加减运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
a
b
a
b
a
b
+
O
A
B
b
C
空间向量的加减法
平面向量
概念
加法
减法
数乘
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量及其加减运算
空间向量
具有大小和方向的量
加法交换律
加法结合律
加法:三角形法则或
平行四边形法则
减法:三角形法则
加法结合律
成立吗?
加法交换律
加法结合律:
a
b
c
a
b
+
c
+
(
)
O
A
B
C
a
b
+
a
b
c
a
b
+
c
+
(
)
O
A
B
C
b
c
+
推广:
(1)首尾相接的若干向量之和,等于由起始
向量的起点指向末尾向量的终点的向量;
(2)首尾相接的若干向量若构成一个封闭图
形,则它们的和为零向量。
a
b
a
b
O
A
B
b
结论:空间任意两个向量都是共面向量,所以它们可用
同一平面内的两条有向线段表示。
因此凡是涉及空间任意两个向量的问题,平面向量中有
关结论仍适用于它们。
思考:它们确定的平面是否唯一?
思考:空间任意两个向量是否可能异面?
例1:已知平行六面体ABCD-A1B1C1D1,化简下列向量
表达式,并标出化简结果的向量。(如图)
A
B
C
D
A1
B1
C1
D1
1.课本P92练习1-3
2.如图,在三棱柱
中,M是
并在图中标出化简得到的向量:
的中点,化简下列各式,
(1)
(2)
(3)
3.已知空间四边形
,连结
,设
分别是
化简下列各表达式,并标出化简结果向量:
(1)
(2)
(3)
的中点,
平面向量
概念
加法
减法
运算
运
算
律
定义
表示法
相等向量
减法:三角形法则
加法:三角形法则或
平行四边形法则
空间向量
具有大小和方向的量
加法交换律
加法结合律
小结
加法交换律
加法结合律
类比思想 数形结合思想
课本P106习题3.1,
A组 第1题(1)、(2)
