5.3平行线的性质课时作业(附答案)
文档属性
| 名称 | 5.3平行线的性质课时作业(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-02 00:00:00 | ||
图片预览




文档简介
5、相交线与平行线课时作业3(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、在同一平面内有三条直线,如果只有两条平行,那么它们的交点个数为( )
A.0?????? ???B.1????? ?????C.2??????? D.3
2、下列说法正确的有(?? )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个????B.2个???? C.3个??? D.4个、
3、如图,下列条件中,能判断直线∥b的是????????????????(? ?? )
A.∠2=∠3??? ????????B.∠1=∠3 C.∠4+∠5=180°??? ????????????????D.∠2=∠4
4、如图, DE∥BC,EF∥AB,图中与∠BFE互补的角共有(?? )
A.3个;???? B.2个;??????C.5个;?????? D.4个.
5、?木工师傅在锯木板时,往往先在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是( ?? ).
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线
D.经过已知直线外一点,有且只有一条直线与已知直线平行
6、如图,把一块直角三角板的直角顶点放在直尺的一边上,??? 如果∠1=32o,那么∠2的度数是(??? )
A. 32o????? B. 58o ????C. 68o?????? D. 60o
7、如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )
A.2对????? B.3对???????? C.4对??????????? D. 5对
8、如图,已知∠DAE=∠B,∠DAB=∠C,则下列结论不成立的是( )
A.AD∥BC? ????? B.∠B=∠C???? C.∠DAB +∠B=180°? D.AB∥CD
9、如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°则∠2的度数等于(??? )
A、?? B、??????? C、 ?? ?D、
10、如图:EA∥DF,AE=DF,要使△AEC≌△DBF,则只要(?????? )
A.AB=CD??? B.EC=BF??? C.∠A=∠D??? D.AB=BC
二、填空题
11、如图,已知l1∥l2,∠1=40°,∠2=55°,则∠3=_____,∠4=____.
12、如图,AB∥CD,且∠1=42°,AE⊥EC于E,则∠2=__________度.
13、如图,将一个长方形纸条折成如图的形状,若已知∠1=130°, 则∠2=_______°。
14、如图,在□ABCD中,∠A=60o,则∠C=????? 度.
15、如图,已知直线,130°,则 ????????度;
16、?如图,方格纸中有四个相同的正方形,则∠1+∠2+∠3等于__________°。
17、若AB∥CD,AB∥EF,则_____∥______,理由是__________________.
18、如图,两平面镜、的夹角为,入射光线AO平行于入射到上,经两次反射后的出射光线O′R平行于,则角等于_________度.
三、作图题
19、(1)根据下列步骤画图并标明相应的字母:(直接在图1中画图)
①以已知线段(图1)为直径画半圆;
②在半圆上取不同于点的一点,连接;
③过点画交半圆于点
(2)尺规作图:(保留作图痕迹,不要求写作法、证明)
已知:(图2).
求作:的平分线.
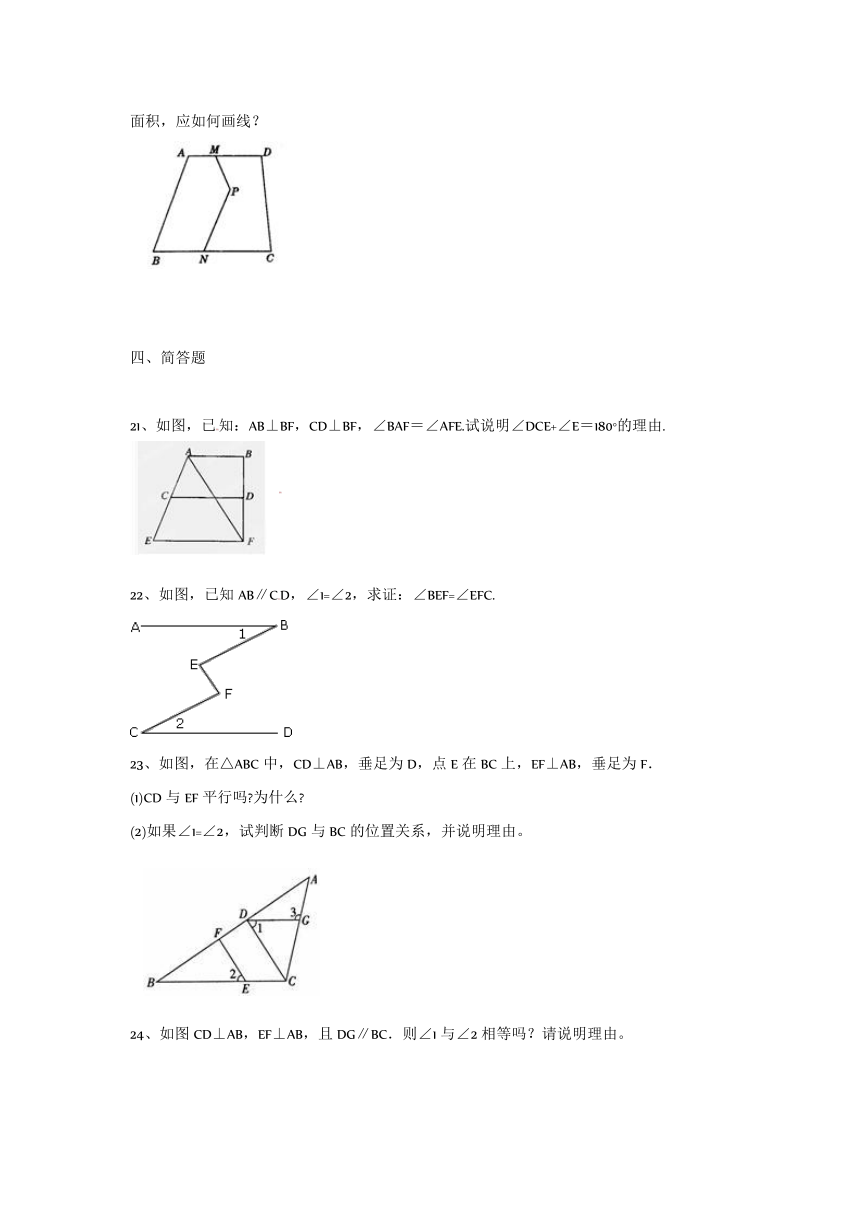
20、如图,欲将一块四方形的耕地中间的一条折路MPN改直,但不能影响道路两边的耕地面积,应如何画线?
四、简答题
21、如图,已知:AB⊥BF,CD⊥BF,∠BAF=∠AFE.试说明∠DCE+∠E=180°的理由.
22、如图,已知AB∥CD,∠1=∠2,求证:∠BEF=∠EFC.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由。
24、如图CD⊥AB,EF⊥AB,且DG∥BC.则∠1与∠2相等吗?请说明理由。
25、平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图a,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD+∠D=∠B.
如图b,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明理由;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点E,如图c,则∠BPD﹑∠B﹑∠D﹑∠BED之间有何数量关系?(不需说明理由);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
26、填空:
如图,已知DE//AC,,试说明.
解:∵(已知)
∴(?????????????????? ???????????)
∵(已知)
∴??????? =????????? (等量代换)
∴(?????????????? ?????????????????)
∴(?????????????????? ???????)
27、如图所示,a∥b,a与c相交,那么b与c相交吗?为什么?
28、已知:如图,∠1=∠2,∠C=∠D,∠A与∠F相等吗?试说明理由.
五、综合题
29、平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图a,点P在AB、CD外部时,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.如图b,将点P移到AB、CD内部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明);;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.(用其它方法也行,)
30、如图,已知直线//,,、在上,且满足,平分.
(1)求的度数.
(2)若平行移动,那么:的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动的过程中,是否存在某种情况,使?若存在,求出其度数;若不存在,请说明理由.
参考答案
一、选择题
1、?C
2、B.
3、B
4、D
5、A
6、B
7、C
8、.B
9、A
10、A.
二、填空题
11、95°、85°
12、
13、65°
14、.
15、50,
16、?135°
17、CD? EF? 平行于同一条直线的两条直线平行
18、60
三、作图题
19、(1)正确完成步骤,各得1分,字母标注完整得1分,满分4分.
(2)说明:以点为圆心,以适当长为半径作弧交于两点
分别以点为圆心,以大于长为半径作弧,
两弧相交于点
?????????????? 作射线
20、连接MN.过P作EF∥MN交AD于E,BC于F.连接MF或NE,则MF或NE为新修的路.
四、简答题
21、
22、
23、?(1)平行(证明略)
(2)DG‖BC(证明略)
24、相等
25、⑴不成立,∠BPD=∠B+∠D;⑵∠BPD=∠B+∠D+∠BED;⑶360°。
26、解:∵(已知)
∴(两直线平行,同位角相等。)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行。)
∴(两直线平行,同位角相等。
27、.解:b与c相交,
假设b与c不相交,
则b∥c,
∵a∥b
∴a∥c,与已知a与c相交矛盾.
28、解:∠A=∠F
∠1=∠2(已知),∠2=∠AHC(对顶角相等)
?∠1=∠AHC(等量代换)
BG∥CH(同位角相等,两直线平行)
?∠ABD=∠C(两直线平行,同位角相等)
又∠C=∠D(已知),
∠ABD=∠D(等量代换)
DF∥AC(内错角相等,两直线平行)
∠A=∠F(两直线平行,内错角相等).
五、综合题
29、(1). ∠BPD=∠B+∠D
(2). ∠BPD=∠B+∠D+∠BQD
(3). 360
30、(1)∵//,∴,∴;
(2)∵//,∴,,∴,∴:=2;
(3)设.
∵//,∴;∵//,∴,∴.若,则,得.∴存在.
姓名:_______________班级:_______________考号:_______________
一、选择题
1、在同一平面内有三条直线,如果只有两条平行,那么它们的交点个数为( )
A.0?????? ???B.1????? ?????C.2??????? D.3
2、下列说法正确的有(?? )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个????B.2个???? C.3个??? D.4个、
3、如图,下列条件中,能判断直线∥b的是????????????????(? ?? )
A.∠2=∠3??? ????????B.∠1=∠3 C.∠4+∠5=180°??? ????????????????D.∠2=∠4
4、如图, DE∥BC,EF∥AB,图中与∠BFE互补的角共有(?? )
A.3个;???? B.2个;??????C.5个;?????? D.4个.
5、?木工师傅在锯木板时,往往先在木板两端用墨盒弹一根墨线然后再锯,这样做的数学道理是( ?? ).
A.两点确定一条直线
B.两点之间线段最短
C.在同一平面内,过直线外或直线上一点,有且只有一条直线垂直于已知直线
D.经过已知直线外一点,有且只有一条直线与已知直线平行
6、如图,把一块直角三角板的直角顶点放在直尺的一边上,??? 如果∠1=32o,那么∠2的度数是(??? )
A. 32o????? B. 58o ????C. 68o?????? D. 60o
7、如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有( )
A.2对????? B.3对???????? C.4对??????????? D. 5对
8、如图,已知∠DAE=∠B,∠DAB=∠C,则下列结论不成立的是( )
A.AD∥BC? ????? B.∠B=∠C???? C.∠DAB +∠B=180°? D.AB∥CD
9、如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°则∠2的度数等于(??? )
A、?? B、??????? C、 ?? ?D、
10、如图:EA∥DF,AE=DF,要使△AEC≌△DBF,则只要(?????? )
A.AB=CD??? B.EC=BF??? C.∠A=∠D??? D.AB=BC
二、填空题
11、如图,已知l1∥l2,∠1=40°,∠2=55°,则∠3=_____,∠4=____.
12、如图,AB∥CD,且∠1=42°,AE⊥EC于E,则∠2=__________度.
13、如图,将一个长方形纸条折成如图的形状,若已知∠1=130°, 则∠2=_______°。
14、如图,在□ABCD中,∠A=60o,则∠C=????? 度.
15、如图,已知直线,130°,则 ????????度;
16、?如图,方格纸中有四个相同的正方形,则∠1+∠2+∠3等于__________°。
17、若AB∥CD,AB∥EF,则_____∥______,理由是__________________.
18、如图,两平面镜、的夹角为,入射光线AO平行于入射到上,经两次反射后的出射光线O′R平行于,则角等于_________度.
三、作图题
19、(1)根据下列步骤画图并标明相应的字母:(直接在图1中画图)
①以已知线段(图1)为直径画半圆;
②在半圆上取不同于点的一点,连接;
③过点画交半圆于点
(2)尺规作图:(保留作图痕迹,不要求写作法、证明)
已知:(图2).
求作:的平分线.
20、如图,欲将一块四方形的耕地中间的一条折路MPN改直,但不能影响道路两边的耕地面积,应如何画线?
四、简答题
21、如图,已知:AB⊥BF,CD⊥BF,∠BAF=∠AFE.试说明∠DCE+∠E=180°的理由.
22、如图,已知AB∥CD,∠1=∠2,求证:∠BEF=∠EFC.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由。
24、如图CD⊥AB,EF⊥AB,且DG∥BC.则∠1与∠2相等吗?请说明理由。
25、平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图a,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD+∠D=∠B.
如图b,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明理由;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点E,如图c,则∠BPD﹑∠B﹑∠D﹑∠BED之间有何数量关系?(不需说明理由);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.
26、填空:
如图,已知DE//AC,,试说明.
解:∵(已知)
∴(?????????????????? ???????????)
∵(已知)
∴??????? =????????? (等量代换)
∴(?????????????? ?????????????????)
∴(?????????????????? ???????)
27、如图所示,a∥b,a与c相交,那么b与c相交吗?为什么?
28、已知:如图,∠1=∠2,∠C=∠D,∠A与∠F相等吗?试说明理由.
五、综合题
29、平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图a,点P在AB、CD外部时,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D.如图b,将点P移到AB、CD内部,则∠BPD、∠B、∠D之间有何数量关系?(不需证明);;
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.(用其它方法也行,)
30、如图,已知直线//,,、在上,且满足,平分.
(1)求的度数.
(2)若平行移动,那么:的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
(3)在平行移动的过程中,是否存在某种情况,使?若存在,求出其度数;若不存在,请说明理由.
参考答案
一、选择题
1、?C
2、B.
3、B
4、D
5、A
6、B
7、C
8、.B
9、A
10、A.
二、填空题
11、95°、85°
12、
13、65°
14、.
15、50,
16、?135°
17、CD? EF? 平行于同一条直线的两条直线平行
18、60
三、作图题
19、(1)正确完成步骤,各得1分,字母标注完整得1分,满分4分.
(2)说明:以点为圆心,以适当长为半径作弧交于两点
分别以点为圆心,以大于长为半径作弧,
两弧相交于点
?????????????? 作射线
20、连接MN.过P作EF∥MN交AD于E,BC于F.连接MF或NE,则MF或NE为新修的路.
四、简答题
21、
22、
23、?(1)平行(证明略)
(2)DG‖BC(证明略)
24、相等
25、⑴不成立,∠BPD=∠B+∠D;⑵∠BPD=∠B+∠D+∠BED;⑶360°。
26、解:∵(已知)
∴(两直线平行,同位角相等。)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行。)
∴(两直线平行,同位角相等。
27、.解:b与c相交,
假设b与c不相交,
则b∥c,
∵a∥b
∴a∥c,与已知a与c相交矛盾.
28、解:∠A=∠F
∠1=∠2(已知),∠2=∠AHC(对顶角相等)
?∠1=∠AHC(等量代换)
BG∥CH(同位角相等,两直线平行)
?∠ABD=∠C(两直线平行,同位角相等)
又∠C=∠D(已知),
∠ABD=∠D(等量代换)
DF∥AC(内错角相等,两直线平行)
∠A=∠F(两直线平行,内错角相等).
五、综合题
29、(1). ∠BPD=∠B+∠D
(2). ∠BPD=∠B+∠D+∠BQD
(3). 360
30、(1)∵//,∴,∴;
(2)∵//,∴,,∴,∴:=2;
(3)设.
∵//,∴;∵//,∴,∴.若,则,得.∴存在.
