5.4平移课时作业(附答案)
文档属性
| 名称 | 5.4平移课时作业(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 165.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-02 00:00:00 | ||
图片预览



文档简介
5、相交线与平行线课时作业4(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
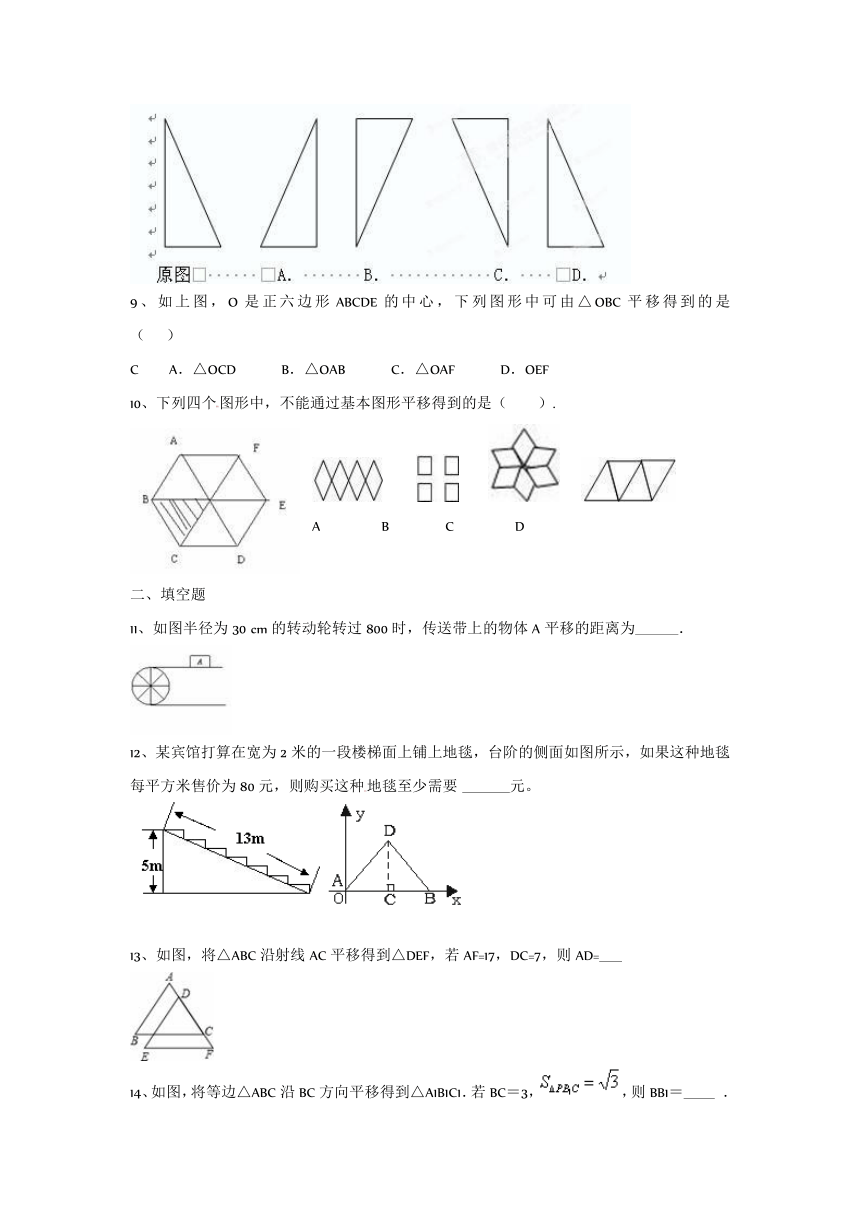
1、?如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是??????(??? )
A.先向下平移3格,再向右平移2格 B.先向下平移3格,再向右平移1格
C.先向下平移2格,再向右平移1格 D.先向下平移2格,再向右平移2格
2、如图,将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长为(????? )
A.12?? ?????B.16 ?? C.20? ? ?D.24
3、?下列四个图形中,不能通过基本图形平移得到的是 (????? )
4、如图所给的图形中只用平移可以得到的有(??? )
A.1个???????????????? B.2个 C. 3个??????????????? D. 4个
5、如图,△ABC和△DEF中,一个三角形经过平移可得到另一个三角形,则下列说法中不正确的是(??????? ).
A、AB∥FD,AB=FD ??????????????B、∠ACB=∠FED
C、BD=CE ?? ??????????????????? ??D、平移距离为线段CD的长度
6、在5×5方格纸中将图⑴中的图形N平移后的位置如图⑵中所示,那么正确的平移方法是 (????? )
A.先向下移动1格,再向左移动1格; B. 先向下移动2格,再向左移动1格;
C. 先向下移动1格,再向左移动2格;D.先向下移动2格,再向左移动2格.
7、在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是?????? (???? )
????? ?????????
A.???????????? B.?????????????C .???????????? D.
8、下列图形中,由原图平移得到的图形是(??? )
9、如上图,O是正六边形ABCDE的中心,下列图形中可由△OBC平移得到的是 (??? )
C A.△OCD B.△OAB C.△OAF D.OEF
10、下列四个图形中,不能通过基本图形平移得到的是( ).
?????? ????????????
A???????????? B??????????? C???????????? D
二、填空题
11、如图半径为30 cm的转动轮转过800时,传送带上的物体A平移的距离为???????? .
12、某宾馆打算在宽为2米的一段楼梯面上铺上地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要?????????? 元。
13、如图,将△ABC沿射线AC平移得到△DEF,若AF=17,DC=7,则AD=
14、如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,,则BB1=??????? .
15、如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是????? .
16、对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位,得到点P的对应点.点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段,其中点A,B的对应点分别为,.如图1,若点A表示的数是,则点表示的数是_______;若点表示的数是2,则点B表示的数是______;已知线段AB上的点E经过上术操作后得到的对应点与点E重合,则点E表示的数是______;
17、在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是
18、?已知△ABC的面积为36,将△ABC沿BC的方向平移到△A/B /C /的位置,使B / 和C重合,连结AC / 交A/C于D,则△C /DC的面积为???????? 。
三、作图题
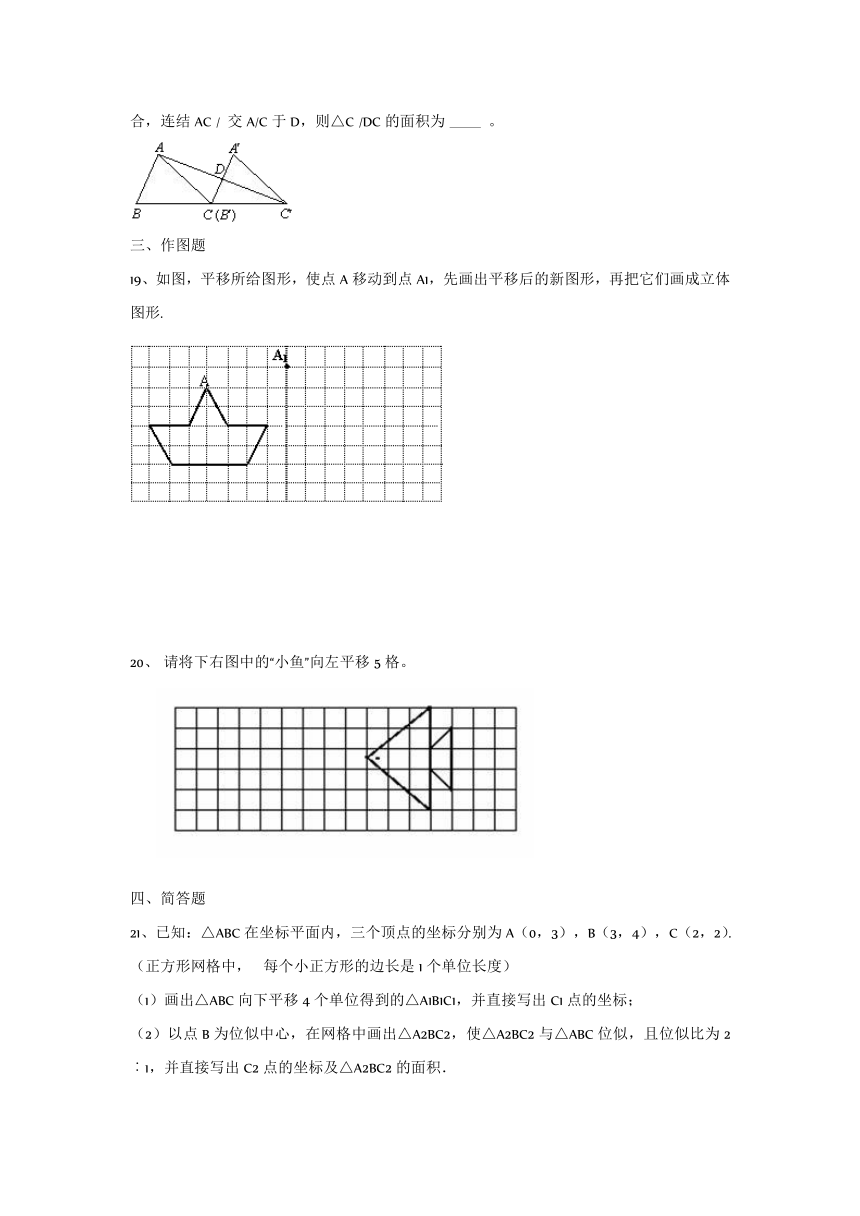
19、如图,平移所给图形,使点A移动到点A1,先画出平移后的新图形,再把它们画成立体图形.
20、?请将下右图中的“小鱼”向左平移5格。
四、简答题
21、已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,? 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
22、在长32m,宽20m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为,求道路的宽.
23、作图:(1)画出图中△ABC的高AD(标注出点D的位置);
(2)画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
(3)根据“图形平移”的性质,得BB1=?????????? cm,
AC与A1C1的关系是:?????????????????? .
24、在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
25、大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?
26、已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米 ∕ 秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:
(1)平移到1.5秒时,重叠部分的面积为????????????? 厘米2.
(2)当S =3.6厘米2时,t=???????? .
(3)当2<t≤4时,S =???????? .
27、如图,这个图形的周长为多少?
五、计算题
28、如图所示,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形绕坐标原点按顺时针方向旋转后得到四边形.
(1)直接写出点的坐标;
(2)将四边形平移,得到四边形,若,画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
参考答案
一、选择题
1、A
2、B
3、D.
4、B
5、D
6、B,
7、D
8、D
9、?D
10、C
二、填空题
11、?40/3π
12、、2720,
13、5
14、1.
15、2。
16、0,3,;
17、
18、?18
三、作图题
19、画立体图形时注意虚线部分.
20、解:如图所示,如右图
四、简答题
21、解:(1)如图,△A1B1C1即为所求,C1(2,-2)。(2)如图,△A2BC2即为所求,C2(1,0),△A2BC2的面积:10
【解析】(1)根据网格结构,找出点A、B、C向下平移4个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标。
(2)延长BA到A2,使AA2=AB,延长BC到C2,使CC2=BC,然后连接A2C2即可,再根据平面直角坐标系写出C2点的坐标,利用△A2BC2所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解:
△A2BC2的面积=6×4-×2×6-×2×4-×2×4=10。
22、如图可把原图变形为?? 2分(不画不扣分)
设道路宽为x,由题意可得:
??????? 5分
解得:(舍)??? 2分
答:道路的宽为2m?????????? 1分
23、
24、考点:作图-平移变换;三角形的面积。
解答:解:(1)图中格点△A′B′C′是由格点△ABC向右平移7个单位长度得到的;
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),则格点△DEF各顶点的坐标分别为D(0,﹣2),E(﹣4,﹣4),F(3,﹣3),
S△DEF=S△DGF+S△GEF=×5×1+×5×1=5
或=7×2﹣×4×2﹣×7×1﹣×3×1=14﹣4﹣﹣=5.
25、距A3千米处
26、(1)3 ;(2)1.8 .提示:列方程2t=3.6;(3)4.
27、如图,通过平移,可知图形的周长20㎝.
五、计算题
28、解:(1)
(2)画出正确图形(见图)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、?如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是??????(??? )
A.先向下平移3格,再向右平移2格 B.先向下平移3格,再向右平移1格
C.先向下平移2格,再向右平移1格 D.先向下平移2格,再向右平移2格
2、如图,将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长为(????? )
A.12?? ?????B.16 ?? C.20? ? ?D.24
3、?下列四个图形中,不能通过基本图形平移得到的是 (????? )
4、如图所给的图形中只用平移可以得到的有(??? )
A.1个???????????????? B.2个 C. 3个??????????????? D. 4个
5、如图,△ABC和△DEF中,一个三角形经过平移可得到另一个三角形,则下列说法中不正确的是(??????? ).
A、AB∥FD,AB=FD ??????????????B、∠ACB=∠FED
C、BD=CE ?? ??????????????????? ??D、平移距离为线段CD的长度
6、在5×5方格纸中将图⑴中的图形N平移后的位置如图⑵中所示,那么正确的平移方法是 (????? )
A.先向下移动1格,再向左移动1格; B. 先向下移动2格,再向左移动1格;
C. 先向下移动1格,再向左移动2格;D.先向下移动2格,再向左移动2格.
7、在图示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是?????? (???? )
????? ?????????
A.???????????? B.?????????????C .???????????? D.
8、下列图形中,由原图平移得到的图形是(??? )
9、如上图,O是正六边形ABCDE的中心,下列图形中可由△OBC平移得到的是 (??? )
C A.△OCD B.△OAB C.△OAF D.OEF
10、下列四个图形中,不能通过基本图形平移得到的是( ).
?????? ????????????
A???????????? B??????????? C???????????? D
二、填空题
11、如图半径为30 cm的转动轮转过800时,传送带上的物体A平移的距离为???????? .
12、某宾馆打算在宽为2米的一段楼梯面上铺上地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要?????????? 元。
13、如图,将△ABC沿射线AC平移得到△DEF,若AF=17,DC=7,则AD=
14、如图,将等边△ABC沿BC方向平移得到△A1B1C1.若BC=3,,则BB1=??????? .
15、如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是????? .
16、对数轴上的点P进行如下操作:先把点P表示的数乘以,再把所得数对应的点向右平移1个单位,得到点P的对应点.点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段,其中点A,B的对应点分别为,.如图1,若点A表示的数是,则点表示的数是_______;若点表示的数是2,则点B表示的数是______;已知线段AB上的点E经过上术操作后得到的对应点与点E重合,则点E表示的数是______;
17、在平面直角坐标系中,规定把一个三角形先沿x轴翻折,再向右平移两个单位称为一次变换,如图,已知等边三角形ABC的顶点B、C的坐标分别是,(-1,-1),(-3,-1),把三角形ABC经过连续9次这样的变换得到三角形A’B’C’,则点A的对应点A’的坐标是
18、?已知△ABC的面积为36,将△ABC沿BC的方向平移到△A/B /C /的位置,使B / 和C重合,连结AC / 交A/C于D,则△C /DC的面积为???????? 。
三、作图题
19、如图,平移所给图形,使点A移动到点A1,先画出平移后的新图形,再把它们画成立体图形.
20、?请将下右图中的“小鱼”向左平移5格。
四、简答题
21、已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,? 每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
22、在长32m,宽20m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为,求道路的宽.
23、作图:(1)画出图中△ABC的高AD(标注出点D的位置);
(2)画出把△ABC沿射线AD方向平移2cm后得到的△A1B1C1;
(3)根据“图形平移”的性质,得BB1=?????????? cm,
AC与A1C1的关系是:?????????????????? .
24、在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
25、大江的一侧有A、B两个工厂,它们有垂直于江边的小路,长度分别为3千米和1千米,设两条小路相距4千米,现在要在江边建立一个抽水站,把水送到A、B两厂去,欲使供水管路最短,抽水站应建在哪里?
26、已知,大正方形的边长为4厘米,小正方形的边长为2厘米,状态如图所示。大正方形固定不动,把小正方形以1厘米 ∕ 秒的速度向大正方形的内部沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S厘米2,完成下列问题:
(1)平移到1.5秒时,重叠部分的面积为????????????? 厘米2.
(2)当S =3.6厘米2时,t=???????? .
(3)当2<t≤4时,S =???????? .
27、如图,这个图形的周长为多少?
五、计算题
28、如图所示,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形绕坐标原点按顺时针方向旋转后得到四边形.
(1)直接写出点的坐标;
(2)将四边形平移,得到四边形,若,画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
参考答案
一、选择题
1、A
2、B
3、D.
4、B
5、D
6、B,
7、D
8、D
9、?D
10、C
二、填空题
11、?40/3π
12、、2720,
13、5
14、1.
15、2。
16、0,3,;
17、
18、?18
三、作图题
19、画立体图形时注意虚线部分.
20、解:如图所示,如右图
四、简答题
21、解:(1)如图,△A1B1C1即为所求,C1(2,-2)。(2)如图,△A2BC2即为所求,C2(1,0),△A2BC2的面积:10
【解析】(1)根据网格结构,找出点A、B、C向下平移4个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标。
(2)延长BA到A2,使AA2=AB,延长BC到C2,使CC2=BC,然后连接A2C2即可,再根据平面直角坐标系写出C2点的坐标,利用△A2BC2所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解:
△A2BC2的面积=6×4-×2×6-×2×4-×2×4=10。
22、如图可把原图变形为?? 2分(不画不扣分)
设道路宽为x,由题意可得:
??????? 5分
解得:(舍)??? 2分
答:道路的宽为2m?????????? 1分
23、
24、考点:作图-平移变换;三角形的面积。
解答:解:(1)图中格点△A′B′C′是由格点△ABC向右平移7个单位长度得到的;
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),则格点△DEF各顶点的坐标分别为D(0,﹣2),E(﹣4,﹣4),F(3,﹣3),
S△DEF=S△DGF+S△GEF=×5×1+×5×1=5
或=7×2﹣×4×2﹣×7×1﹣×3×1=14﹣4﹣﹣=5.
25、距A3千米处
26、(1)3 ;(2)1.8 .提示:列方程2t=3.6;(3)4.
27、如图,通过平移,可知图形的周长20㎝.
五、计算题
28、解:(1)
(2)画出正确图形(见图)
