18-2勾股定理逆定理(第2课时)课件—沪科版数学八年级下册(19张ppt)
文档属性
| 名称 | 18-2勾股定理逆定理(第2课时)课件—沪科版数学八年级下册(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 17:18:55 | ||
图片预览





文档简介
(共19张PPT)
沪科版 数学 八年级 下册
18.2 勾股定理的逆定理
第二课时
1、进一步加深对勾股定理与其逆定理之间关系的认识.,理解勾股数并能记住一些常见勾股数
2. 学会将实际问题转化成用勾股定理的逆定理解决的数学问题.
进而运用勾股定理及其逆定理解决实际生活中的问题.
教学目标
知识回顾
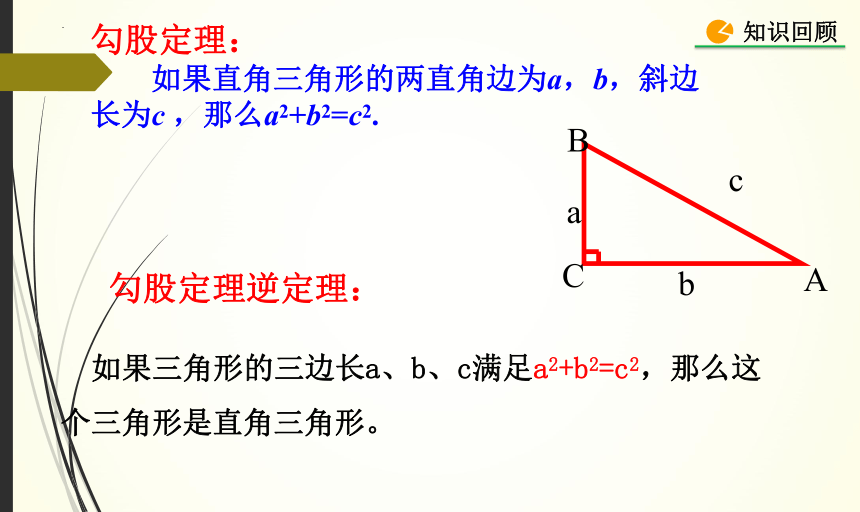
勾股定理:
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2.
a
b
c
C
B
A
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
勾股定理逆定理:
判定一个三角形是直角三角形的方法
有一个角是直角的三角形是直角三角形.
角:
边:
如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形
4
知识回顾
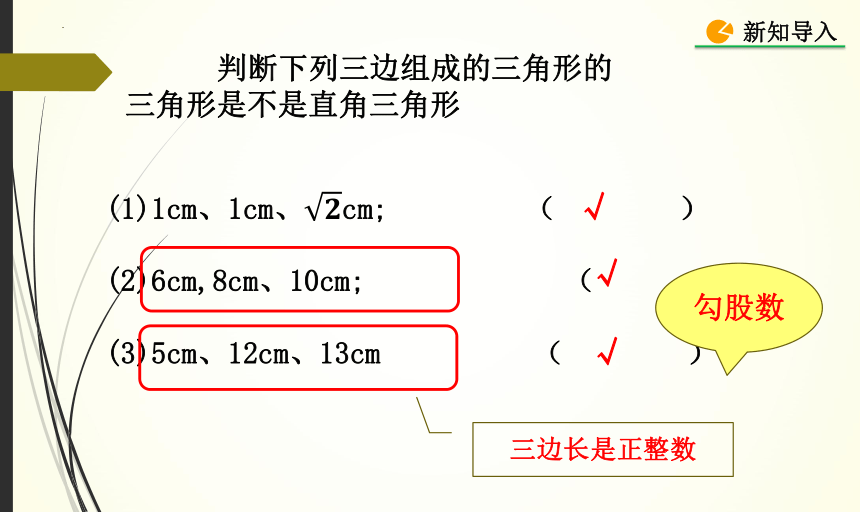
(1)1cm、1cm、cm; ( )
(2)6cm,8cm、10cm; ( )
(3)5cm、12cm、13cm ( )
判断下列三边组成的三角形的三角形是不是直角三角形
新知导入
√
√
√
三边长是正整数
勾股数
勾 股 数
成为直角三角形三条边长的三个正整数,称为勾股数
勾股数
三个正整数a、b、c
a2+b2=c2
新知讲解
常见勾股数:
3,4,5;
5,12,13
6,8,10
7,24,25
8,15,17
9,40,41
10,24,26
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
已知m,n是任意给定的正整数(m>n),
求证:m2+n2,2mn,m2-n2为勾股数
证:
新知讲解
∵(m2-n2) +(2mn)
=m4-2m n +n4+4mn
=m4+2m n +n4
=( m2+n2 )
∴ 以m2+n2,2mn,m2-n2为边的三角形是直角三角形
∵ m,n是任意给定的正整数(m>n)
∴ m2+n2,2mn,m2-n2为三个正整数
∴ m2+n2,2mn,m2-n2为勾股数
毕达哥拉斯数
试一试:
利用毕达哥拉斯数m2+n2,2mn,m2-n2写勾股数,
新知讲解
当m=5,n=3,勾股数为:34,30,16
当m=7,n=5,勾股数为:74,70, 24
当m=3,n=2,勾股数为:13,12, 5
当m=6,n=5,勾股数为:61,60, 11
很神奇哦!
例1、如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。
证明:∵AD是BC边上的中线,
∴BD=CD=BC=5㎝
∵在△ABD中,
AB=13,BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形,即AD⊥BC
∴AB=AC(垂直平分线上的点到两端点距离相等)
A
B
C
D
例题讲解
┓
例2、如图,在操场上竖直立着一根长为2m的测影竿CD,早晨测得它的影长BD为4m,中 午测得它的影长 AD为1m,且B、D、A在 同一条直线上,则A、B、C三点能否构成直角三角形?为什么?
A
B
C
D
∵在Rt△BDC中,BD=4,CD=2,
∴BC2=BD2+CD2=42+22=20,
同理,AC2=5,
又∵AB=BD+AD=5
∴AB2=52=25
∴AB2=BC2+AC2
∴△ABC为直角三角形
解:
A、B、C三点能构成直角三角形
理由如下:
┓
例题讲解
例题讲解
例3、如图,是一块四边形绿地示意图, AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90°
C
D
24
20
15
7
B
A
求:绿地ABCD的面积
解:连结BD
∵BC=20,CD=15,∠ C=90°
∴BD =CD +CB =15 +20 =625(勾股定理)
∵AB=24,AD=7
∴AD +AB =24 +7 =625
∴BD =AD +AB =625
∴∠DAB=90°(勾股定理逆定理)
∴SDABC=S△DAB+S△DCB=
如图,有一块地,已知,AD=4m,CD=3∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
变式练习1:
A
B
C
3
4
13
12
D
提示:
连结AC
∴S=S△ACB-S△ADC
=
由勾股定理逆定理得: ∠ACB=90°
由勾股定理得: AC=5
如图四边形ABCD的周长为42,AB=AD=12,∠A=60°,BC=13,求∠ADC的度数.
变式练习2:
C
D
B
A
提示:连结BD
你解对了吗
∠ADC=150°
1、我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
解:∵52+122=132,
∴三条边长分别为5里,12里,13里,构成了直角三角形,
∴这块沙田面积为:
×5×500×12×500=7500000(平方米)=7.5(平方千米).
提升练习
A
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52 +1 …
2、张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b ,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__________,b=__________,c=__________.
(2)以a,b,c为边长的三角形是否为直角三角形
提升练习
解:
以a,b,c为边长的三角形是直角三角形
.理由如下:
∵a2+b2=(n2-1)2+4n2=n4-2n2+1+4n2
=n4+2n2+1=(n2+1)2=c2,
∴以a,b,c为边长的三角形是直角三角形.
n2-1
2n
n2+1
3、在△ABC中,AB=12,AC=9,BC=15,则△ABC的面积等于( )
A.108 B.90 C.180 D.54
提升练习
D
4、已知︱x-12︱+(y-13)2与z2-10z+25互为相反数,则以x、y、z为三边的三角形是___________三角形.
直角
5、在△ABC中,AB=2k,AC=2k-1,BC=3,当k=______时,∠C=90°.
2.5
6.给出一组式子:
32+42=52, 82+62=102,
152+82=172, 242+102=262,….
请你依据规律直接写出第五个式子:
______________________.
352+122=372
提升练习
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
提升练习
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理的逆定理
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b2课堂小结:
沪科版 数学 八年级 下册
18.2 勾股定理的逆定理
第二课时
1、进一步加深对勾股定理与其逆定理之间关系的认识.,理解勾股数并能记住一些常见勾股数
2. 学会将实际问题转化成用勾股定理的逆定理解决的数学问题.
进而运用勾股定理及其逆定理解决实际生活中的问题.
教学目标
知识回顾
勾股定理:
如果直角三角形的两直角边为a,b,斜边长为c ,那么a2+b2=c2.
a
b
c
C
B
A
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形。
勾股定理逆定理:
判定一个三角形是直角三角形的方法
有一个角是直角的三角形是直角三角形.
角:
边:
如果三角形的三边长a,b,c满足 a2+b2=c2,那么这个三角形是直角三角形
4
知识回顾
(1)1cm、1cm、cm; ( )
(2)6cm,8cm、10cm; ( )
(3)5cm、12cm、13cm ( )
判断下列三边组成的三角形的三角形是不是直角三角形
新知导入
√
√
√
三边长是正整数
勾股数
勾 股 数
成为直角三角形三条边长的三个正整数,称为勾股数
勾股数
三个正整数a、b、c
a2+b2=c2
新知讲解
常见勾股数:
3,4,5;
5,12,13
6,8,10
7,24,25
8,15,17
9,40,41
10,24,26
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
已知m,n是任意给定的正整数(m>n),
求证:m2+n2,2mn,m2-n2为勾股数
证:
新知讲解
∵(m2-n2) +(2mn)
=m4-2m n +n4+4mn
=m4+2m n +n4
=( m2+n2 )
∴ 以m2+n2,2mn,m2-n2为边的三角形是直角三角形
∵ m,n是任意给定的正整数(m>n)
∴ m2+n2,2mn,m2-n2为三个正整数
∴ m2+n2,2mn,m2-n2为勾股数
毕达哥拉斯数
试一试:
利用毕达哥拉斯数m2+n2,2mn,m2-n2写勾股数,
新知讲解
当m=5,n=3,勾股数为:34,30,16
当m=7,n=5,勾股数为:74,70, 24
当m=3,n=2,勾股数为:13,12, 5
当m=6,n=5,勾股数为:61,60, 11
很神奇哦!
例1、如图:在Δ ABC中,AB=13㎝,BC=10㎝,BC边上的中线AD=12㎝,求证:AB=AC。
证明:∵AD是BC边上的中线,
∴BD=CD=BC=5㎝
∵在△ABD中,
AB=13,BD=5,AD=12
∴ BD2+AD2=52+122=169=AB2
∴ △ABD是直角三角形,即AD⊥BC
∴AB=AC(垂直平分线上的点到两端点距离相等)
A
B
C
D
例题讲解
┓
例2、如图,在操场上竖直立着一根长为2m的测影竿CD,早晨测得它的影长BD为4m,中 午测得它的影长 AD为1m,且B、D、A在 同一条直线上,则A、B、C三点能否构成直角三角形?为什么?
A
B
C
D
∵在Rt△BDC中,BD=4,CD=2,
∴BC2=BD2+CD2=42+22=20,
同理,AC2=5,
又∵AB=BD+AD=5
∴AB2=52=25
∴AB2=BC2+AC2
∴△ABC为直角三角形
解:
A、B、C三点能构成直角三角形
理由如下:
┓
例题讲解
例题讲解
例3、如图,是一块四边形绿地示意图, AB长24米,BC长20米,CD长15米,DA长7米,∠ C=90°
C
D
24
20
15
7
B
A
求:绿地ABCD的面积
解:连结BD
∵BC=20,CD=15,∠ C=90°
∴BD =CD +CB =15 +20 =625(勾股定理)
∵AB=24,AD=7
∴AD +AB =24 +7 =625
∴BD =AD +AB =625
∴∠DAB=90°(勾股定理逆定理)
∴SDABC=S△DAB+S△DCB=
如图,有一块地,已知,AD=4m,CD=3∠ADC=90°,AB=13m,BC=12m。求这块地的面积。
变式练习1:
A
B
C
3
4
13
12
D
提示:
连结AC
∴S=S△ACB-S△ADC
=
由勾股定理逆定理得: ∠ACB=90°
由勾股定理得: AC=5
如图四边形ABCD的周长为42,AB=AD=12,∠A=60°,BC=13,求∠ADC的度数.
变式练习2:
C
D
B
A
提示:连结BD
你解对了吗
∠ADC=150°
1、我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米 C.75平方千米 D.750平方千米
解:∵52+122=132,
∴三条边长分别为5里,12里,13里,构成了直角三角形,
∴这块沙田面积为:
×5×500×12×500=7500000(平方米)=7.5(平方千米).
提升练习
A
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52 +1 …
2、张老师在一次“探究性学习”课中,设计了如下数表:
(1)请你分别观察a,b ,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__________,b=__________,c=__________.
(2)以a,b,c为边长的三角形是否为直角三角形
提升练习
解:
以a,b,c为边长的三角形是直角三角形
.理由如下:
∵a2+b2=(n2-1)2+4n2=n4-2n2+1+4n2
=n4+2n2+1=(n2+1)2=c2,
∴以a,b,c为边长的三角形是直角三角形.
n2-1
2n
n2+1
3、在△ABC中,AB=12,AC=9,BC=15,则△ABC的面积等于( )
A.108 B.90 C.180 D.54
提升练习
D
4、已知︱x-12︱+(y-13)2与z2-10z+25互为相反数,则以x、y、z为三边的三角形是___________三角形.
直角
5、在△ABC中,AB=2k,AC=2k-1,BC=3,当k=______时,∠C=90°.
2.5
6.给出一组式子:
32+42=52, 82+62=102,
152+82=172, 242+102=262,….
请你依据规律直接写出第五个式子:
______________________.
352+122=372
提升练习
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
提升练习
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数
勾股定理的逆定理
在 ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则 ABC为直角三角形;
若a2 +b2>c2, 则 ABC为锐角三角形;
若a2 +b2
