沪科版七年级下册 7.3 一元一次不等式组课件(共31张PPT)
文档属性
| 名称 | 沪科版七年级下册 7.3 一元一次不等式组课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 561.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 00:00:00 | ||
图片预览







文档简介
(共32张PPT)
第7章 一元一次不等式与不等式组
请你来说说,你是怎样来理解不等式的
1:在下列数学表达式中找出不等式 :
√
√
√
√
√
√
用不等号连接而成的数学式子叫不等式
在下列数学表达式中找出一元一次不等式 :
一元一次不等式又如何理解
√
√
不等式的解集又如何理解
不等式的两边都是整式,只含有一个未知数,且未知数的次数是1的不等式,叫做一元一次不等式
能使不等式成立的未知数的值的全体,
叫做不等式的解集,简称不等式的解
根据下列数量关系列不等式:
⑴、a不是正数。
⑵、x与y的一半的差大于-3。
⑶、y的70%与5的和是非负数。
⑷、3与x的倒数的差小于5。
⑸、a的立方根不等于a。
上述不等式中那些是一元一次不等式 ( )
⑴、 ⑶
1、某饮料瓶上有这样的字样:保质期18个月。如果用X(单位:月)表示保质期,那么该饮料的保质期可以用不等式表示为 。
2、根据数量关系列不等式:
(1)足球比赛中,每队上场队员人数p不超过11;
(2)y的平方是非负数;
(3)x的3倍与2的和大于4;
(4)y与12的差比它的5倍小;
(5)m与1的相反数的和不小于3.
X≤18
P≤11
y2≥0
3x+2>4
y-12<5y
m-1≥3
写出下列不等式
填一填
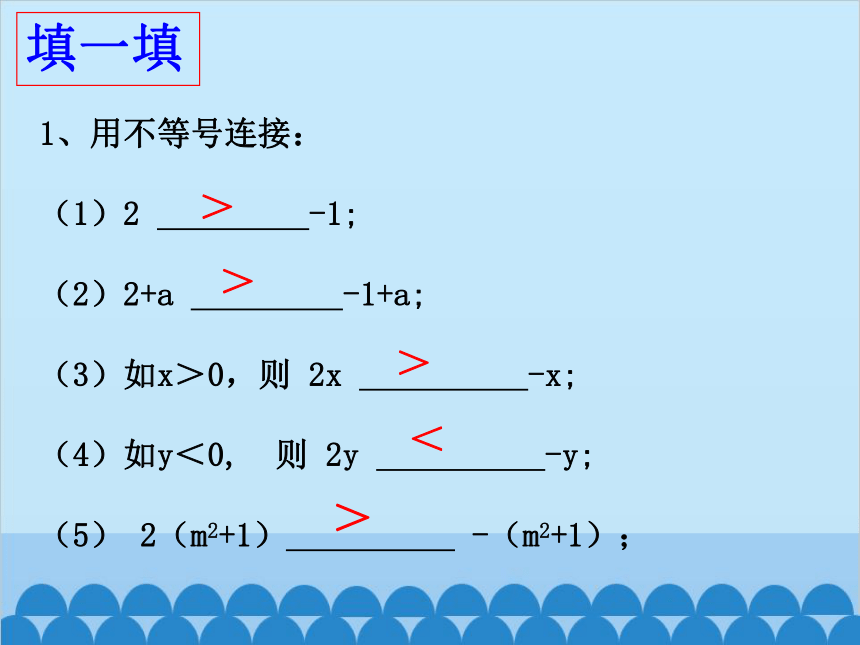
1、用不等号连接:
(1)2 -1;
(2)2+a -1+a;
(3)如x>0,则 2x -x;
(4)如y<0, 则 2y -y;
(5) 2(m2+1) -(m2+1);
>
>
>
<
>
4、由不等式(m-5)x> m-5变形为x< 1,则m需满足的条件是 ,
3、若a >b,且a、b为有理数,则am2 bm2
6、若不等式组 无解,
则a的取值范围是 ;
x> a+2
x<3a-2
2、若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5、已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 ,
0≤x≤5
≥
m<5
12≤m < 15
a ≤ 2
A
B
C
6
8
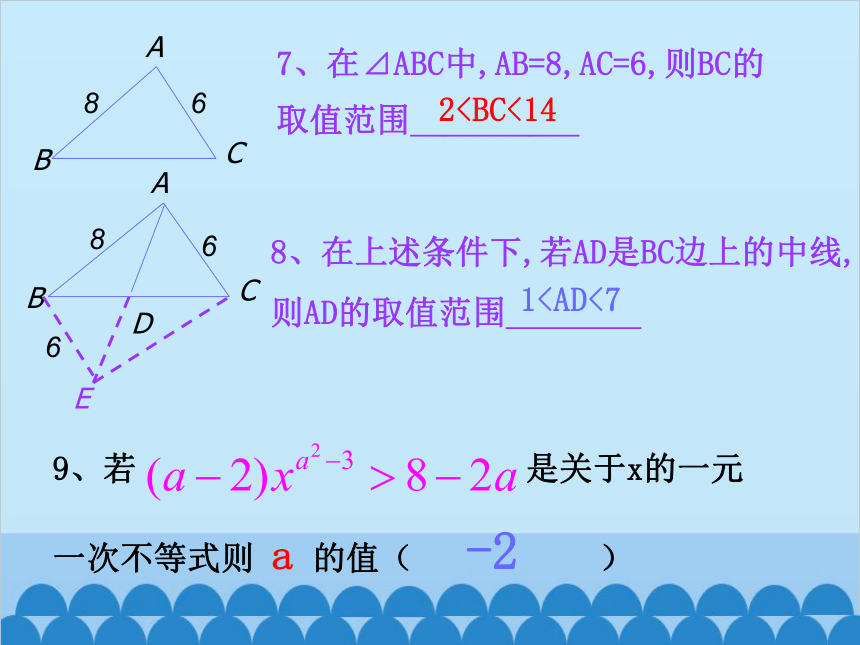
7、在⊿ABC中,AB=8,AC=6,则BC的
取值范围__________
21A
B
C
D
8、在上述条件下,若AD是BC边上的中线,
则AD的取值范围________
8
6
6
E
9、若 是关于x的一元
一次不等式则 a 的值( )
-2
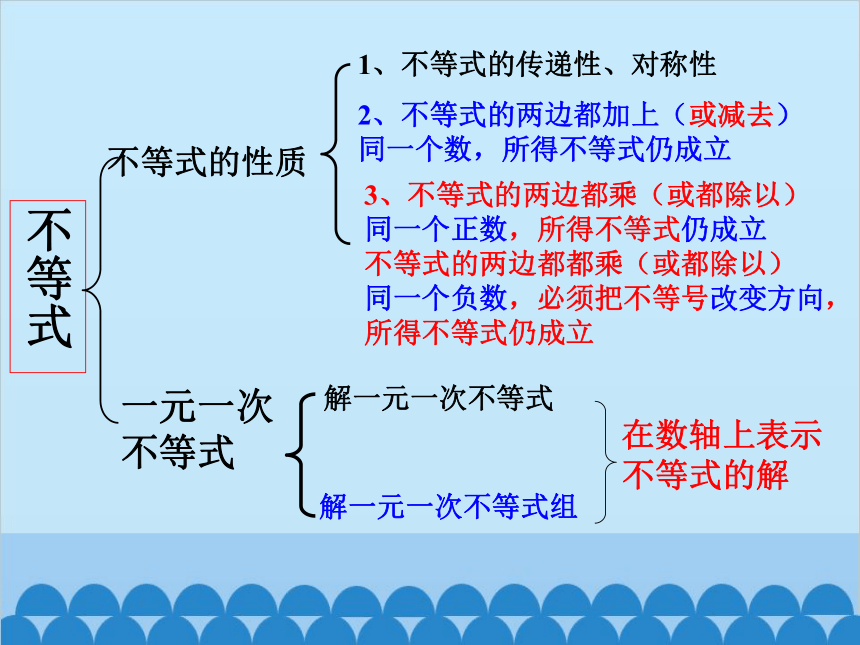
不等式
不等式的性质
1、不等式的传递性、对称性
2、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
3、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,所得不等式仍成立
一元一次
不等式
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式的解
例1、解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
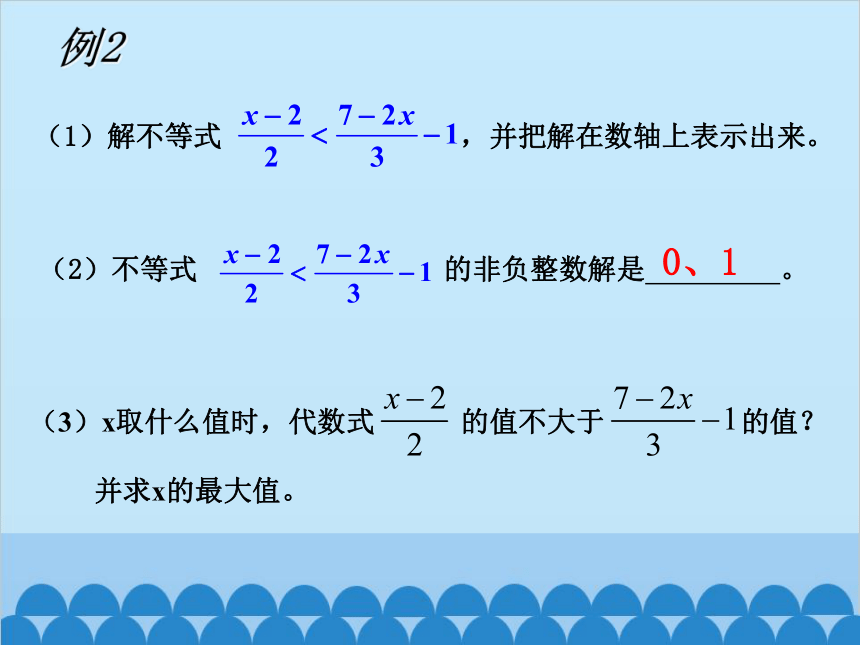
(1)解不等式 ,并把解在数轴上表示出来。
(2)不等式 的非负整数解是 。
0、1
(3)x取什么值时,代数式 的值不大于 的值?
并求x的最大值。
例2
大大取大
的解集是
当a>b时,
X>a
X>b
X>a
小小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大取中间
的解集是
当a>b时,
X<a
X≥b
b ≤ X<a
大小等同取等值
X=a
的解集是
X≥a
X≤a
不等式组
大大小小则无解
的解集是
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
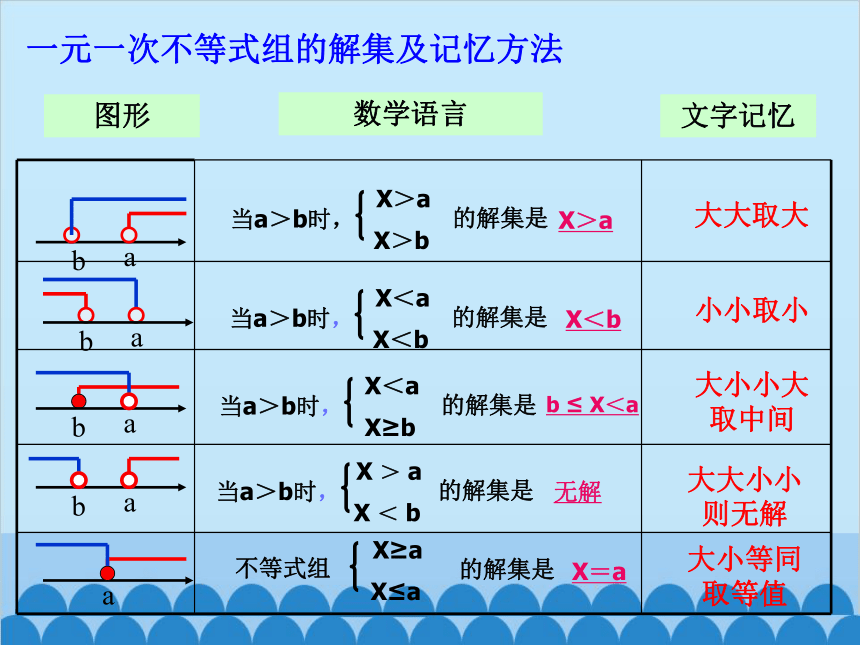
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
a
b
解:由(1)得:2x+6>X+5 则 x>-1
由(2)得x-2
0则x
2
-12
用数轴表示:
2
0
-1
例3、解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点
从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
15
2<m<5
m≤13
例4
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5、y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5例6、 求使方程组:
x+y=m+2
4x+5y=6m+3
的解x ,y都是正数的m的取值范围
1.若关于X的方程2x+3k=1的解是负数,则K的取值范围是
X是非负数
2.如果关于x的方程3x+a=x+4的解是个非负数,
求a的取值范围。
使方程组 的解 x 、 y都
是正数,
求a的取值范围。
解: (1)×5-(2),得:x=7+a (3)
把(3)代入(1),得:y=-5 -2a
1、解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
是同解不等式?如果存在,求出整数m和不等式
的解集;如果不存在,请说明理由。
与
2、是否存在整数m,使关于x的不等式
x>-8
3、已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:不等式3x-a≥0的负整数解为-1,-2,求a的范围
4、不等式组 无解,求a的范围
{
x>2a-1
x<3
{
x≥2a-1
x<3
不等式组
无解,求a的范围
变式一:
{
x≥2a-1
x ≤ 3
不等式组
无解,求a的范围
变式二:
5、已知,不等式组 3(x-4)< 2(4x+5)-2
>
①求此不等式组的整数解
②若上述整数解满足方程ax-3=3a-x,求a的值
③ 在① ②的条件下,求代数式 的值
例、王海贷款5万元去做生意,贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满.
1.设有x间宿舍,请写出x应满足的不等式组;
2.可能有多少间宿舍,多少名学生
思路分析
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满, 这 是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 6x>4x+19
6(x-1)<4x+19
解得: 18.5因为x是整数,所以x=10,11,12.
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
做一做:
1、一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x) ≥85
解得: x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1= y2时,150x=160x-160, 解得x=16;
y1 >y2时,150x>160x-160, 解得x<16;
y1< y2时,150x<160x-160, 解得x>16;
2、某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
3、某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
即 10x>220
x>22
4、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
第7章 一元一次不等式与不等式组
请你来说说,你是怎样来理解不等式的
1:在下列数学表达式中找出不等式 :
√
√
√
√
√
√
用不等号连接而成的数学式子叫不等式
在下列数学表达式中找出一元一次不等式 :
一元一次不等式又如何理解
√
√
不等式的解集又如何理解
不等式的两边都是整式,只含有一个未知数,且未知数的次数是1的不等式,叫做一元一次不等式
能使不等式成立的未知数的值的全体,
叫做不等式的解集,简称不等式的解
根据下列数量关系列不等式:
⑴、a不是正数。
⑵、x与y的一半的差大于-3。
⑶、y的70%与5的和是非负数。
⑷、3与x的倒数的差小于5。
⑸、a的立方根不等于a。
上述不等式中那些是一元一次不等式 ( )
⑴、 ⑶
1、某饮料瓶上有这样的字样:保质期18个月。如果用X(单位:月)表示保质期,那么该饮料的保质期可以用不等式表示为 。
2、根据数量关系列不等式:
(1)足球比赛中,每队上场队员人数p不超过11;
(2)y的平方是非负数;
(3)x的3倍与2的和大于4;
(4)y与12的差比它的5倍小;
(5)m与1的相反数的和不小于3.
X≤18
P≤11
y2≥0
3x+2>4
y-12<5y
m-1≥3
写出下列不等式
填一填
1、用不等号连接:
(1)2 -1;
(2)2+a -1+a;
(3)如x>0,则 2x -x;
(4)如y<0, 则 2y -y;
(5) 2(m2+1) -(m2+1);
>
>
>
<
>
4、由不等式(m-5)x> m-5变形为x< 1,则m需满足的条件是 ,
3、若a >b,且a、b为有理数,则am2 bm2
6、若不等式组 无解,
则a的取值范围是 ;
x> a+2
x<3a-2
2、若y= -x+7,且2≤y≤7,则x的取值范围是 ,
5、已知不等式3x-m ≤0有4个正整数解,则m的取值范围是 ,
0≤x≤5
≥
m<5
12≤m < 15
a ≤ 2
A
B
C
6
8
7、在⊿ABC中,AB=8,AC=6,则BC的
取值范围__________
2
B
C
D
8、在上述条件下,若AD是BC边上的中线,
则AD的取值范围________
8
6
6
E
9、若 是关于x的一元
一次不等式则 a 的值( )
-2
不等式
不等式的性质
1、不等式的传递性、对称性
2、不等式的两边都加上(或减去)
同一个数,所得不等式仍成立
3、不等式的两边都乘(或都除以)
同一个正数,所得不等式仍成立
不等式的两边都都乘(或都除以)
同一个负数,必须把不等号改变方向,所得不等式仍成立
一元一次
不等式
解一元一次不等式
解一元一次不等式组
在数轴上表示
不等式的解
例1、解下列不等式(组)并在数轴上表示出来。
(1) -
-5
解:去分母得:4(2x-1)-2(10x+1)
15x-60
移项,合并同类项 得:-27x
-54
x
2
在数轴上表示如图所示:
1
2
0
(1)解不等式 ,并把解在数轴上表示出来。
(2)不等式 的非负整数解是 。
0、1
(3)x取什么值时,代数式 的值不大于 的值?
并求x的最大值。
例2
大大取大
的解集是
当a>b时,
X>a
X>b
X>a
小小取小
的解集是
当a>b时,
X<a
X<b
X<b
大小小大取中间
的解集是
当a>b时,
X<a
X≥b
b ≤ X<a
大小等同取等值
X=a
的解集是
X≥a
X≤a
不等式组
大大小小则无解
的解集是
当a>b时,
X > a
X < b
无解
文字记忆
数学语言
图形
一元一次不等式组的解集及记忆方法
a
b
a
b
a
b
a
a
b
解:由(1)得:2x+6>X+5 则 x>-1
由(2)得x-2
0则x
2
-1
用数轴表示:
2
0
-1
例3、解不等式组
2(x+3)>x+5 (1)
0 (2)
(1)解一元一次不等式组 2x+3≥4 ①
3x-2≤2x+3 ②
(2)不等式组4≤3x-2≤2x+3的所有整数解的和是 。
(3)如果4,3m-2,2m+3这三个数在数轴上所对应的点
从左到右依次排列,则m的取值范围是 。
(4)不等式组 2x+3≥m 的解是 x≥5,则的取值范围
3x-2≥2x+3
是 。
15
2<m<5
m≤13
例4
解这个不等式,得
∴y的正整数解是:1,2,3,4。
例5、y取何正整数时,代数式2(y-1)的值不大于10-4(y-3)的值。
解:根据题意列出不等式:
解:解方程组得:
x=-m+7
y=2m-5
因为它的解是正数,所以:
-m+7>0
2m-5>0
所以
2.5
x+y=m+2
4x+5y=6m+3
的解x ,y都是正数的m的取值范围
1.若关于X的方程2x+3k=1的解是负数,则K的取值范围是
X是非负数
2.如果关于x的方程3x+a=x+4的解是个非负数,
求a的取值范围。
使方程组 的解 x 、 y都
是正数,
求a的取值范围。
解: (1)×5-(2),得:x=7+a (3)
把(3)代入(1),得:y=-5 -2a
1、解关于x的不等式: k(x+3)>x+4;
解:去括号,得kx+3k>x+4;
移项得kx-x > 4 -3k ; 得(k-1)x > 4 -3k ;
若k-1=0, 即k=1时,0>1不成立,
∴不等式无解。
若k-1>0,即k>1时,
若k-1<0,即k<1时,
。
是同解不等式?如果存在,求出整数m和不等式
的解集;如果不存在,请说明理由。
与
2、是否存在整数m,使关于x的不等式
x>-8
3、已知不等式3x-a≤0的正整数解是1,2,3,求a的范围
变式1:不等式3x-a<0的正整数解为1,2,3,求a的范围
变式2:不等式3x-a>0的负整数解为-1,-2,求a的范围
变式3:不等式3x-a≥0的负整数解为-1,-2,求a的范围
4、不等式组 无解,求a的范围
{
x>2a-1
x<3
{
x≥2a-1
x<3
不等式组
无解,求a的范围
变式一:
{
x≥2a-1
x ≤ 3
不等式组
无解,求a的范围
变式二:
5、已知,不等式组 3(x-4)< 2(4x+5)-2
>
①求此不等式组的整数解
②若上述整数解满足方程ax-3=3a-x,求a的值
③ 在① ②的条件下,求代数式 的值
例、王海贷款5万元去做生意,贷款月利息10‰ .他决定在半年内利用赚来的钱一次性还清贷款的本息。问王海平均每个月至少要赚多少钱?(精确到100元)
月利息=本金×利率
本息=本金+利息
解:设王海平均每月要赚x元钱。根据题意得
6x≥50000+50000×10‰×6
解得
答:王海平均每个月至少要赚8900元钱。
根据题意得取x=8900
一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满.
1.设有x间宿舍,请写出x应满足的不等式组;
2.可能有多少间宿舍,多少名学生
思路分析
这里有X间宿舍,每间住4人,剩下19人,因此学生人数为4X+19人,若每间住6人,则有一间住不满, 这 是什么不等关系呢 你明白吗
6
6
6
4X+19
0人到6人之间
最后一间宿舍
6
(X-1)间宿舍
列不等式组为: 0<4x+19-6(x-1)<6
可以看出: 0<最后一间宿舍住的人数<6
解: 设有x间宿舍,根据题意得不等式组:
0<4x+19-6(x-1)<6
即: 6x>4x+19
6(x-1)<4x+19
解得: 18.5
因此可能有10间宿舍,59名学生或11间宿舍,63名学生或12间宿舍,67名学生.
做一做:
1、一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分,在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解:设小答对了x道题,则得4x分,另有(25-x)道要扣分,而小明评为优秀,即小明的得分应大于或等于85分,
4x-(25-x) ≥85
解得: x≥22
所以,小明到少答对了22道题,他可能答对22,23,24或25道题。
y1=200×0.75x,即y1=150x,
y2=200×0.8(x-1),即y2=160x-160,
y1= y2时,150x=160x-160, 解得x=16;
y1 >y2时,150x>160x-160, 解得x<16;
y1< y2时,150x<160x-160, 解得x>16;
2、某单位计划在新年期间组织员工到某地旅游,参如旅游的人数估计为10~25人,甲、乙两家旅行社的服务质量相同,且报价都是每人200元,经过协商,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可先免去一位游客的旅游费用,其余游客八折优惠,该单位选择哪一定旅行社支付的旅游费用较少?
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需的费用为y1,选择乙旅行社时,所需的费用为y2,则:
所以,当人数为16人时,甲、乙两家旅行社的收费相同;当人数为17~25人时,选择甲旅行社费用较少;当人数为10~15人时,选择乙旅行社费用较少。
3、某商品的零售价是每件50元,进价是每件35元。经核算,每天商店的各种费用(包括房租、售货员工资等)是120元,还需把商品售出价的10%上缴税款,问商店每天需要出售多少件这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
解:设商店每天出售该商品x件。根据题意得
(50-35-50×10%)x-120>100
解得
答:商店每天需要出售23件或23件以上这样的商品,才能保证商店每天获纯利润在100元以上(不包括100元)?
即 10x>220
x>22
4、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件,已知生产一件A产品需要甲原料9kg,乙原料3kg,生产一件B产品需要甲原料4kg,乙原料10kg,
(1)设生产X件A种产品,写出X应满足的不等式组。
(2)有哪几种符合的生产方案?
(3)若生产一件A产品可获利700元,生产一件B产品可获利1200元,那么采用哪种生产方案可使生产A、B两种产品的总获利最大?最大利润是多少?
