人教版数学七年级下册数学活动课件(24张ppt)
文档属性
| 名称 | 人教版数学七年级下册数学活动课件(24张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 08:49:21 | ||
图片预览





文档简介
(共25张PPT)
R·七年级下册
数学活动
——求完全立方数的立方根
学习目标:
(1)会求完全立方数的立方根.
(2)勤于动脑,善于归纳,学习领会那些常见计算技巧,提高运算能力.
学习重、难点:
求完全立方数的立方根的方法和步骤.
情景导入
本节课中,活动1要求制作正方体和圆柱形纸盒,在制作过程中需要用到在数轴上作出表示特殊无理数的点等知识.活动2是求一些完全立方数的立方根,通过立方运算确定立方根的位数和各个数位上的数是解题的关键.
探究新知
活动1
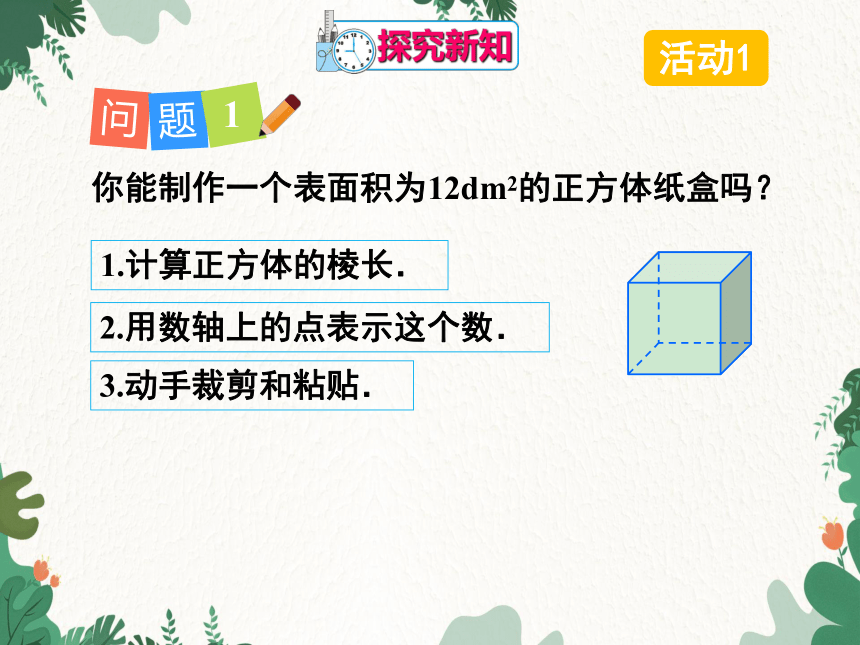
你能制作一个表面积为12dm2的正方体纸盒吗?
1.计算正方体的棱长.
2.用数轴上的点表示这个数.
3.动手裁剪和粘贴.
问
题
1
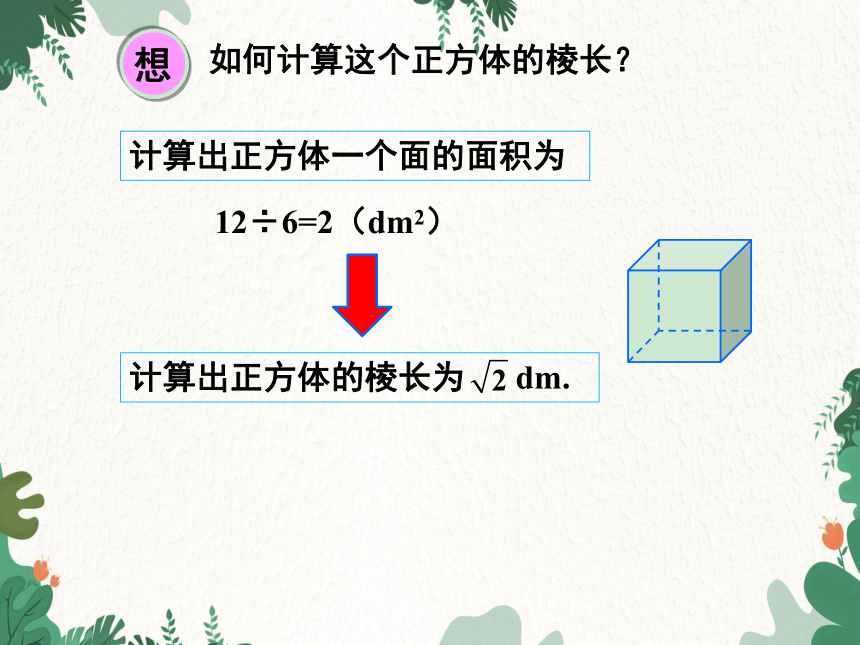
如何计算这个正方体的棱长?
计算出正方体一个面的面积为
12÷6=2(dm2)
计算出正方体的棱长为 dm.
想
如何画出长度为 的线段?
画一条数轴,单位长度为1 dm.
01
0
1
2
想
02
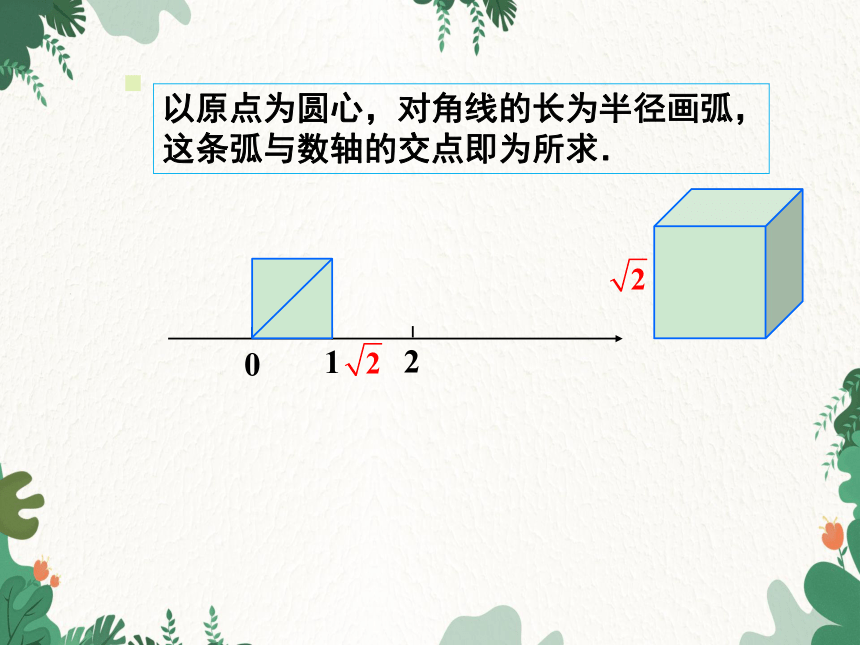
如图,在数轴上作出边长为1 dm的正方形,并画出该正方形的对角线.
0
1
2
03
以原点为圆心,对角线的长为半径画弧,这条弧与数轴的交点即为所求.
0
1
2
问
题
2
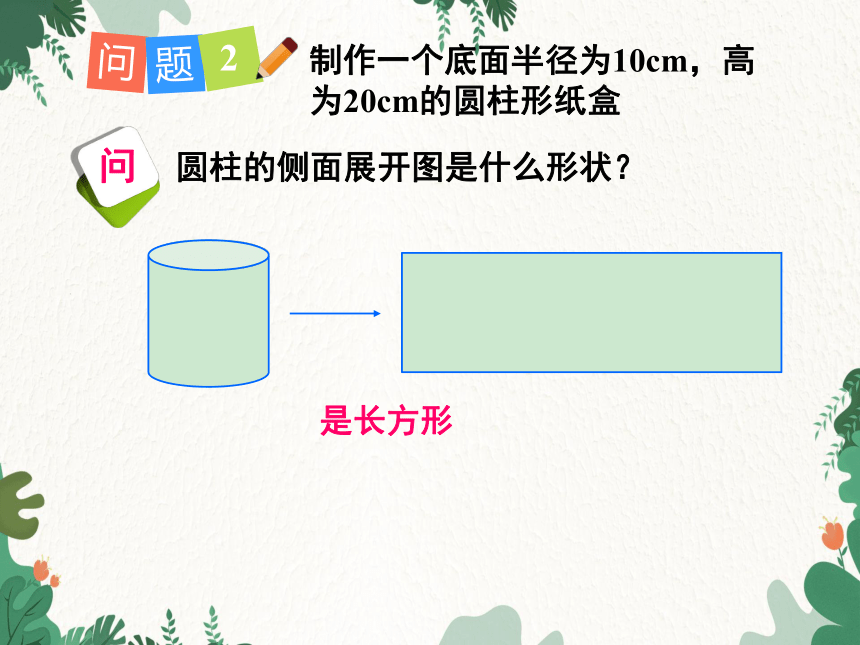
制作一个底面半径为10cm,高为20cm的圆柱形纸盒
问
圆柱的侧面展开图是什么形状?
是长方形
问
这个侧面展开图各边的长分别是多少?
20cm
20cm
宽=圆柱体的高=20cm
长=圆柱体的底面周长=(2×10×π)cm
10cm
(2×10×π)cm
活动2
据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59 319,希望求它的立方根.华罗庚脱口而出:39. 邻座的乘客十分惊奇,忙问计算的奥妙.
想
你知道华罗庚是怎样迅速准确地计算出来的吗?
确定结果的位数.
确定各个数位上的数字.
1
由103=1000,1003=1000000,你能确定
是几位数吗?
因为103 < 59319 < 1003
所以10 < < 100
所以 是个两位数
2
由59319的个位上的数是9,你能确定
的个位上的数是几吗?
在0 ~ 9中,只有9的立方的末位数字是9,所以 的个位上的数是9.
3
如果划去59319后面的三位319得到数59,而33=27,43=64,由此你能确定
的十位上的数是几吗?
因为33 < 59 < 43所以 的十位上的数是3.
练习
1.已知19683,110592都是完全立方数,按上面的方法求得:
= ______
= ______
27
48
2.你能依照上面的方法求完全平方数1369,6724的算术平方根吗?
= ______
= ______
37
82
基础巩固
随堂演练
1.已知4096,39304,140608都是完全立方数,不用计算器求 =____, =____, =____.
2. 已知 =1.603, =3.454,
=7.441,则 =_______,
=_______.
16
34
52
0.7441
34.54
3. 已知 =2.030, =6.419,则
=_______, =______.
4. 已知2304,7225,15129都是完全平方数,不用计算器求 =____, =
____, =____.
0.6419
203.0
48
85
123
综合运用
5.求 的近似值(精确到0.01).
解:∵23=8,33=27,而8<10<27,∴2 < < 3.
∵2.13=9.261,2.23=10.648,而9.261<10<10.648,
∴2.1 < < 2.2
∵2.153=9.938375,2.163=10.077696,
而9.938375<10<10.077696,∴2.15 < < 2.16.
∵2.1543=9.993948,2.1553=10.007874,
而2.1543更接近10.
∴ ≈2.15.
课堂小结
通过本节课的学习你能快速地算出一个数的平方根或立方根了吗?
伸
延
展
拓
从图书、网络等方面搜集一些巧算立方根或平方根的资料,与同学们分享一下.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
在本节课教学过程中,通过教学活动2,调动了学生的积极性,引导学生观察思考,逐步质疑,逐渐由旧知归纳出新知,既培养学生的动手能力,又为实数学习打下基础.
R·七年级下册
数学活动
——求完全立方数的立方根
学习目标:
(1)会求完全立方数的立方根.
(2)勤于动脑,善于归纳,学习领会那些常见计算技巧,提高运算能力.
学习重、难点:
求完全立方数的立方根的方法和步骤.
情景导入
本节课中,活动1要求制作正方体和圆柱形纸盒,在制作过程中需要用到在数轴上作出表示特殊无理数的点等知识.活动2是求一些完全立方数的立方根,通过立方运算确定立方根的位数和各个数位上的数是解题的关键.
探究新知
活动1
你能制作一个表面积为12dm2的正方体纸盒吗?
1.计算正方体的棱长.
2.用数轴上的点表示这个数.
3.动手裁剪和粘贴.
问
题
1
如何计算这个正方体的棱长?
计算出正方体一个面的面积为
12÷6=2(dm2)
计算出正方体的棱长为 dm.
想
如何画出长度为 的线段?
画一条数轴,单位长度为1 dm.
01
0
1
2
想
02
如图,在数轴上作出边长为1 dm的正方形,并画出该正方形的对角线.
0
1
2
03
以原点为圆心,对角线的长为半径画弧,这条弧与数轴的交点即为所求.
0
1
2
问
题
2
制作一个底面半径为10cm,高为20cm的圆柱形纸盒
问
圆柱的侧面展开图是什么形状?
是长方形
问
这个侧面展开图各边的长分别是多少?
20cm
20cm
宽=圆柱体的高=20cm
长=圆柱体的底面周长=(2×10×π)cm
10cm
(2×10×π)cm
活动2
据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59 319,希望求它的立方根.华罗庚脱口而出:39. 邻座的乘客十分惊奇,忙问计算的奥妙.
想
你知道华罗庚是怎样迅速准确地计算出来的吗?
确定结果的位数.
确定各个数位上的数字.
1
由103=1000,1003=1000000,你能确定
是几位数吗?
因为103 < 59319 < 1003
所以10 < < 100
所以 是个两位数
2
由59319的个位上的数是9,你能确定
的个位上的数是几吗?
在0 ~ 9中,只有9的立方的末位数字是9,所以 的个位上的数是9.
3
如果划去59319后面的三位319得到数59,而33=27,43=64,由此你能确定
的十位上的数是几吗?
因为33 < 59 < 43所以 的十位上的数是3.
练习
1.已知19683,110592都是完全立方数,按上面的方法求得:
= ______
= ______
27
48
2.你能依照上面的方法求完全平方数1369,6724的算术平方根吗?
= ______
= ______
37
82
基础巩固
随堂演练
1.已知4096,39304,140608都是完全立方数,不用计算器求 =____, =____, =____.
2. 已知 =1.603, =3.454,
=7.441,则 =_______,
=_______.
16
34
52
0.7441
34.54
3. 已知 =2.030, =6.419,则
=_______, =______.
4. 已知2304,7225,15129都是完全平方数,不用计算器求 =____, =
____, =____.
0.6419
203.0
48
85
123
综合运用
5.求 的近似值(精确到0.01).
解:∵23=8,33=27,而8<10<27,∴2 < < 3.
∵2.13=9.261,2.23=10.648,而9.261<10<10.648,
∴2.1 < < 2.2
∵2.153=9.938375,2.163=10.077696,
而9.938375<10<10.077696,∴2.15 < < 2.16.
∵2.1543=9.993948,2.1553=10.007874,
而2.1543更接近10.
∴ ≈2.15.
课堂小结
通过本节课的学习你能快速地算出一个数的平方根或立方根了吗?
伸
延
展
拓
从图书、网络等方面搜集一些巧算立方根或平方根的资料,与同学们分享一下.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
在本节课教学过程中,通过教学活动2,调动了学生的积极性,引导学生观察思考,逐步质疑,逐渐由旧知归纳出新知,既培养学生的动手能力,又为实数学习打下基础.
