数学高中苏教版选修(2-3)1.2《排列》课件
文档属性
| 名称 | 数学高中苏教版选修(2-3)1.2《排列》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 101.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-03 08:42:45 | ||
图片预览






文档简介
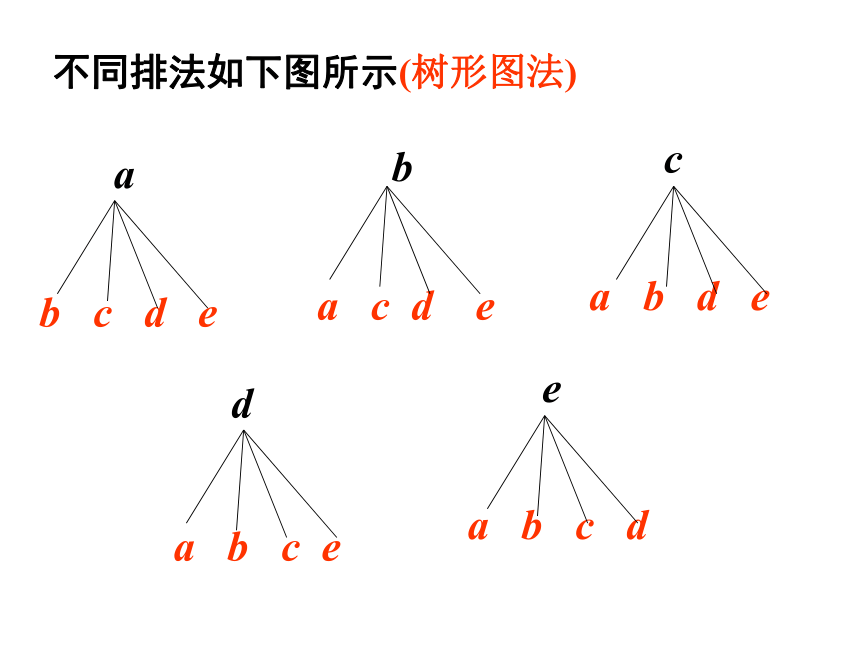
课件21张PPT。1.2 排 列(2)知识回顾①什么叫做从n个不同元素中取出m个元素的一个排列? 从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.②两个不同的排列:排列问题,是取出元素后,还要按一定的顺序排成一列,只要排列顺序不同,就视为完成这件事的两种不同的方法.③由排列的定义可知,排列与元素的顺序有关,也就是说与位置有关的问题才能归结为排列问题.当元素较少时,可以根据排列的意义写出所有的排列.(树形图) 问题:有a、b、c、d、e 5个火车站,都有往返列车,问车站间共需要准备几种火车票?分析:由于涉及到起点、终点站,所以题中含“有序”,问题可转化为:从5个元素中,取2个元素的排列问题.问题情境ab c d e不同排法如下图所示(树形图法)ba c d eca b d eda b c eea b c d1. 排列数的定义 从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数.
用符号 表示问题1 求从3个不同的元素中取出2个元素的排列数. 记为 问题2 求从4个不同的元素中取出3个元素的排列数. 记为 数学概念“排列”和“排列数”有什么区别和联系?探究:从n个不同的元素中取出2个元素的排列
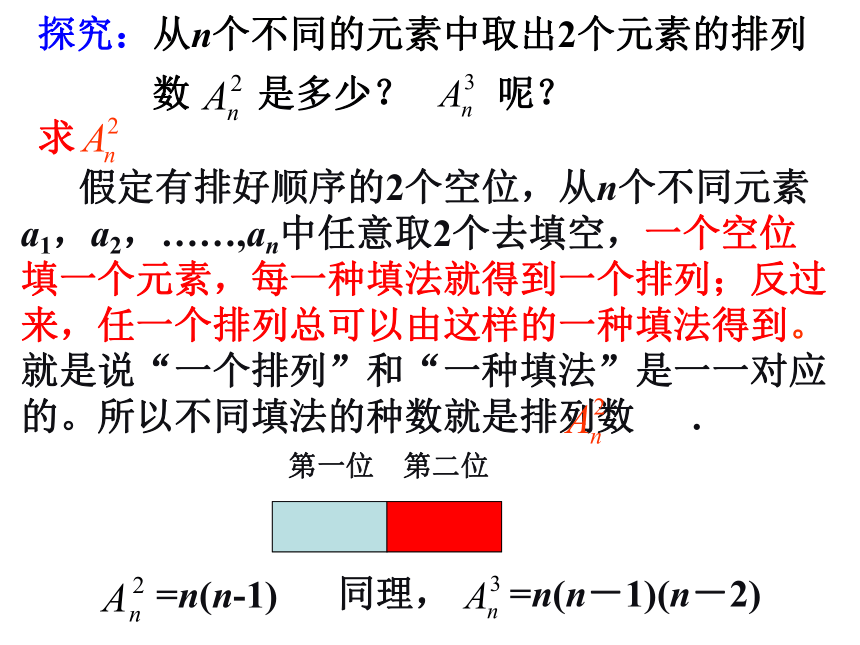
数 是多少? 呢?求 假定有排好顺序的2个空位,从n个不同元素a1,a2,……,an中任意取2个去填空,一个空位填一个元素,每一种填法就得到一个排列;反过来,任一个排列总可以由这样的一种填法得到。就是说“一个排列”和“一种填法”是一一对应的。所以不同填法的种数就是排列数 .=n(n-1)同理, =n(n-1)(n-2)2. 排列数公式的推导求 :从n个不同的元素中取出m个元素的排列数. 假定有排好顺序的m个空位,从n个不同元素a1,a2,……,an中任意取m个去填空,一个空位填一个元素,每一种填法就得到一个排列;反过来,任一个排列总可以由这样的一种填法得到。所以不同填法的种数就是排列数 .2. 排列数公式的推导分m步:
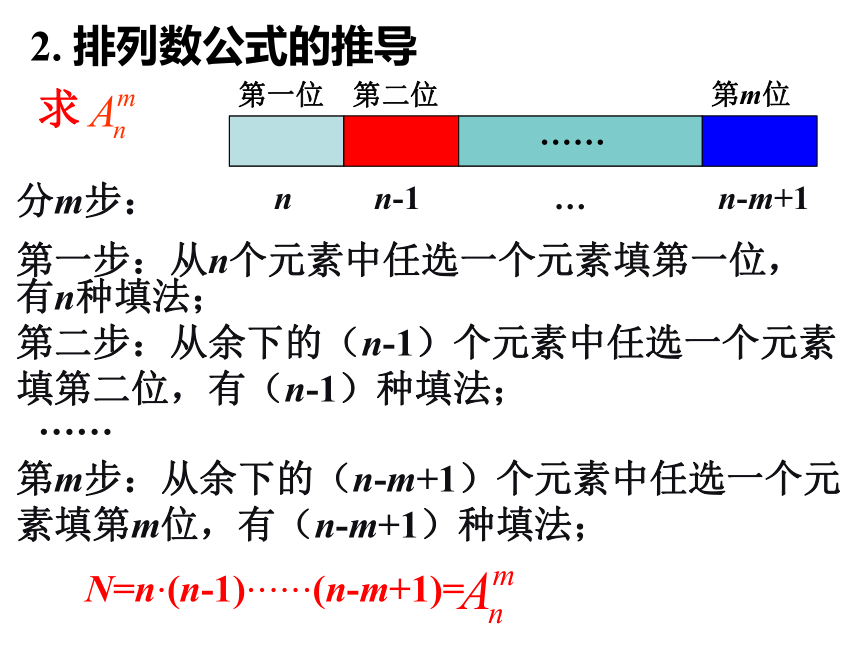
第一步:从n个元素中任选一个元素填第一位, 有n种填法;第二步:从余下的(n-1)个元素中任选一个元素填第二位,有(n-1)种填法;……第m步:从余下的(n-m+1)个元素中任选一个元素填第m位,有(n-m+1)种填法;N=n·(n-1)······(n-m+1)=nn-1n-m+1…求排列数公式:1. n,m∈N*,m≤n;评注:2. 特征:公式右边中第一个因数是n,后面的每个因数都比它前面一个因数少1,最后一个因数为n-m+1,共有m个因数相乘.排列数公式的阶乘形式:当m=n时,由正整数1到n的连乘积,叫做阶乘,用 表示. 即:规定:0!=1.数学运用例1 计算:(1) ; (2) ; (3) . 变式2:若n∈N,则
用排列数符号为 .变式3:若 ,则 n = .数学运用例2 求证: (n>m) . 排列数公式:点评:①排列数公式的推导是“建构”框图填空来解决的,这是一种简单的建模方法; ②一般情况下,第一个公式常用于计算,第二个公式常用于化简、证明; ③对于“m、n∈N+ ,m≤n”这个条件要留意,往往是一些含有未知数的排列数计算、解方程等问题的隐含条件.课堂练习11. 求证: . 例3 解方程:解:原方程可化为:
2x·(2x-1)·(2x-2)=100·x·(x-1)
∵x≠0且x≠1,
∴2x-1=25, 解得 x=13.
经检验 x=13 是原方程的根.数学运用例4 求证:证明:右边=即证.注:n·(n-1)!=n! , (m+3)·(m+2)!=(m+3)! ……数学运用例5 求值:解:数学运用课堂练习2随堂检测课堂小结 “一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.一是“取出元素”;
二是“按照一定顺序排列”,1. 排列的定义中包含两个基本内容:2. 掌握排列数公式的推导方法;
3. 了解简单的建模方法;
4. 区分两个排列数公式的不同适用范围.1. 课时作业
2.《教学与测试》课后作业
用符号 表示问题1 求从3个不同的元素中取出2个元素的排列数. 记为 问题2 求从4个不同的元素中取出3个元素的排列数. 记为 数学概念“排列”和“排列数”有什么区别和联系?探究:从n个不同的元素中取出2个元素的排列
数 是多少? 呢?求 假定有排好顺序的2个空位,从n个不同元素a1,a2,……,an中任意取2个去填空,一个空位填一个元素,每一种填法就得到一个排列;反过来,任一个排列总可以由这样的一种填法得到。就是说“一个排列”和“一种填法”是一一对应的。所以不同填法的种数就是排列数 .=n(n-1)同理, =n(n-1)(n-2)2. 排列数公式的推导求 :从n个不同的元素中取出m个元素的排列数. 假定有排好顺序的m个空位,从n个不同元素a1,a2,……,an中任意取m个去填空,一个空位填一个元素,每一种填法就得到一个排列;反过来,任一个排列总可以由这样的一种填法得到。所以不同填法的种数就是排列数 .2. 排列数公式的推导分m步:
第一步:从n个元素中任选一个元素填第一位, 有n种填法;第二步:从余下的(n-1)个元素中任选一个元素填第二位,有(n-1)种填法;……第m步:从余下的(n-m+1)个元素中任选一个元素填第m位,有(n-m+1)种填法;N=n·(n-1)······(n-m+1)=nn-1n-m+1…求排列数公式:1. n,m∈N*,m≤n;评注:2. 特征:公式右边中第一个因数是n,后面的每个因数都比它前面一个因数少1,最后一个因数为n-m+1,共有m个因数相乘.排列数公式的阶乘形式:当m=n时,由正整数1到n的连乘积,叫做阶乘,用 表示. 即:规定:0!=1.数学运用例1 计算:(1) ; (2) ; (3) . 变式2:若n∈N,则
用排列数符号为 .变式3:若 ,则 n = .数学运用例2 求证: (n>m) . 排列数公式:点评:①排列数公式的推导是“建构”框图填空来解决的,这是一种简单的建模方法; ②一般情况下,第一个公式常用于计算,第二个公式常用于化简、证明; ③对于“m、n∈N+ ,m≤n”这个条件要留意,往往是一些含有未知数的排列数计算、解方程等问题的隐含条件.课堂练习11. 求证: . 例3 解方程:解:原方程可化为:
2x·(2x-1)·(2x-2)=100·x·(x-1)
∵x≠0且x≠1,
∴2x-1=25, 解得 x=13.
经检验 x=13 是原方程的根.数学运用例4 求证:证明:右边=即证.注:n·(n-1)!=n! , (m+3)·(m+2)!=(m+3)! ……数学运用例5 求值:解:数学运用课堂练习2随堂检测课堂小结 “一定顺序”就是与位置有关,这也是判断一个问题是不是排列问题的重要标志.一是“取出元素”;
二是“按照一定顺序排列”,1. 排列的定义中包含两个基本内容:2. 掌握排列数公式的推导方法;
3. 了解简单的建模方法;
4. 区分两个排列数公式的不同适用范围.1. 课时作业
2.《教学与测试》课后作业
