数学高中苏教版选修(2-2)3.1《数系的扩充》课件
文档属性
| 名称 | 数学高中苏教版选修(2-2)3.1《数系的扩充》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-03 08:43:12 | ||
图片预览






文档简介
课件16张PPT。3.1 数系的扩充
学习目标:
了解数系的扩充过程, 理解虚数及有关概念.1 位科学院士,2 位影视导演,3 位知名医生,4 位公司总裁,……0 个害群之马.这里的 0,1,2,3,4,5,… 是什么数?5 位县委书记,通常,我们把一个数集连同相应的运算及结
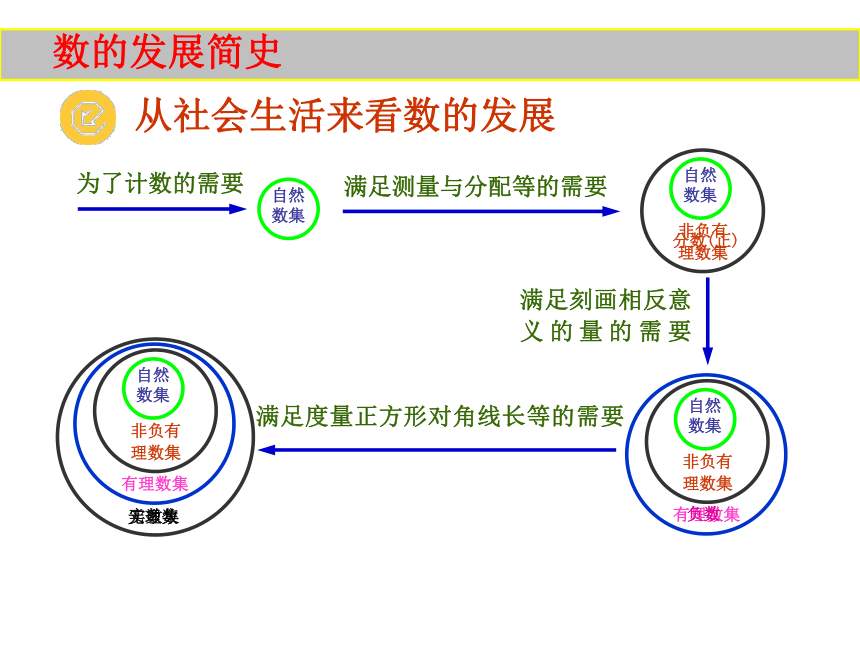
构叫做一个数系.为了计数的需要满足刻画相反意
义的量的需要满足测量与分配等的需要有理数集满足度量正方形对角线长等的需要实数集数的发展简史从社会生活来看数的发展分数(正)非负有
理数集负数无理数为了计数的需要满足除法的需要满足减法的需要Q满足非负数开方的需要R数的发展简史从数学内部来看数的发展负数Z分数无理数满足解x-3=4等方程的需要满足解3x-2=0等方程的需要满足解x+6=5等方程的需要Q满足解x2-2=0等方程的需要R数的发展简史从解方程的角度来看数的发展负数Z分数无理数◆ 为什么要对数集进行一次又一次地扩充?反思与启示进步性!◆ 每一次对数集进行扩充时,是如何解决矛盾的?引新性!◆ 每次数集扩充之后,有没有影响到原有的运算及性质?包容性!可以解决某些在原来数集中不能解决的矛盾.新的数集都是在原来数集的基础上“添加”了一种新的数得到的.在新的数集中,原有的运算及性质仍然适用.新添加的数可以与原有的数进行四则运算,
且进行四则运算时,原有的加法、乘法运算
律仍然成立.数集扩充到实数集之后,是不是所有的方程都有解了呢?新的矛盾如何再对实数集进行合理地扩充呢?问题2 找出这些方程中的最简单的一个方程探究与发现问题3 如果想要这个最简单的方程也有解,你打算怎么办?问题1 试着求解这几个方程, 它们在实数集里没有
解的原因是什么?--imaginary--假想的、虚构的i——虚数单位问题4 根据数系扩充的原则,你认为要给 i 作哪些规定?探究与发现我们引入一个新数 i ,叫做虚数单位,并规定:(1)i 2 =-1.(2)实数可以与 i 进行四则运算,进行四则运算时,
原有的加法、乘法运算律仍然成立.探究与发现问题5 -i 是不是也是方程 x2 = -1 的解呢?问题6 引入虚数单位 i 后,上述三个方程的解分别是什么?问题7 这些根可统一写成什么样的形式?问题4 根据数系扩充的原则,你认为要给 i 作哪些规定?问题2 找出这些方程中的最简单的一个方程问题3 如果想要这个最简单的方程也有解,你打算怎么办?问题1 试着求解这几个方程, 它们在实数集里没有
解的原因是什么?(1)复数的定义:形如 a+bi(a,b∈R) 的数,我们称之为复数.(2)复数的表示:复数通常用字母z表示,即z =a+bi(a,b∈R).a + b i (a,b∈R)叫做复数z的代数形式. 实部虚部复数的有关概念你能列举一些复数吗?复数的有关概念(3)复数的分类:对于复数z=a+bi(a,b ∈R):◆当b=0时,复数z=a,此时它就是实数.◆当b≠0时,复数z=a+bi,此时称之为虚数.特别地,当a=0且b≠0时,复数z=bi,此时称之为纯虚数.(4)复数集:全体复数所组成的集合,叫做复数集,记作C.复数集C与前面的数集之间的关系如何?例1说出刚才所列举复数的实部与虚部,变式判断下列说法是否正确:(1)复数 iπ 的实部为0,虚部是 iπ.(2)复数 i lg1 是纯虚数.(3)复数2+(1+i)i的实部是2,虚部是(1+i).反思(1)复数z=a+bi(a,b∈R)的虚部仅指单独的实数b,不能
含有i.(2)复数的实部与虚部必须是实数.应用与反思 并指出哪些是实数,
哪些是虚数,哪些是纯虚数?例2实数m取什么值时,复数z=m(m-1)+(m-1)i是:
(1)实数? (2)虚数? (3)纯虚数?变式(4)当实数m取什么值时,复数z=0?反思复数z=a+bi(a,b∈R)是纯虚数a=0两个复数相等,当且仅当它们的实部和虚部分别相等,即a+bi = c+di(a,b,c,d∈R).应用与反思??例3已知(x+y)+(x-2y)i =(2x-5)+(3x+y)i,求实数x,y的值.反思(2)一个复数方程可裂变为两个实数方程,因而可求两
个未知数.(1)解决复数问题的基本思想:应用与反思 复数问题实数化.复数的有关概念善于抓主要矛盾复数系的扩充同样遵循复数系还需要扩充吗?知识与启迪
学习目标:
了解数系的扩充过程, 理解虚数及有关概念.1 位科学院士,2 位影视导演,3 位知名医生,4 位公司总裁,……0 个害群之马.这里的 0,1,2,3,4,5,… 是什么数?5 位县委书记,通常,我们把一个数集连同相应的运算及结
构叫做一个数系.为了计数的需要满足刻画相反意
义的量的需要满足测量与分配等的需要有理数集满足度量正方形对角线长等的需要实数集数的发展简史从社会生活来看数的发展分数(正)非负有
理数集负数无理数为了计数的需要满足除法的需要满足减法的需要Q满足非负数开方的需要R数的发展简史从数学内部来看数的发展负数Z分数无理数满足解x-3=4等方程的需要满足解3x-2=0等方程的需要满足解x+6=5等方程的需要Q满足解x2-2=0等方程的需要R数的发展简史从解方程的角度来看数的发展负数Z分数无理数◆ 为什么要对数集进行一次又一次地扩充?反思与启示进步性!◆ 每一次对数集进行扩充时,是如何解决矛盾的?引新性!◆ 每次数集扩充之后,有没有影响到原有的运算及性质?包容性!可以解决某些在原来数集中不能解决的矛盾.新的数集都是在原来数集的基础上“添加”了一种新的数得到的.在新的数集中,原有的运算及性质仍然适用.新添加的数可以与原有的数进行四则运算,
且进行四则运算时,原有的加法、乘法运算
律仍然成立.数集扩充到实数集之后,是不是所有的方程都有解了呢?新的矛盾如何再对实数集进行合理地扩充呢?问题2 找出这些方程中的最简单的一个方程探究与发现问题3 如果想要这个最简单的方程也有解,你打算怎么办?问题1 试着求解这几个方程, 它们在实数集里没有
解的原因是什么?--imaginary--假想的、虚构的i——虚数单位问题4 根据数系扩充的原则,你认为要给 i 作哪些规定?探究与发现我们引入一个新数 i ,叫做虚数单位,并规定:(1)i 2 =-1.(2)实数可以与 i 进行四则运算,进行四则运算时,
原有的加法、乘法运算律仍然成立.探究与发现问题5 -i 是不是也是方程 x2 = -1 的解呢?问题6 引入虚数单位 i 后,上述三个方程的解分别是什么?问题7 这些根可统一写成什么样的形式?问题4 根据数系扩充的原则,你认为要给 i 作哪些规定?问题2 找出这些方程中的最简单的一个方程问题3 如果想要这个最简单的方程也有解,你打算怎么办?问题1 试着求解这几个方程, 它们在实数集里没有
解的原因是什么?(1)复数的定义:形如 a+bi(a,b∈R) 的数,我们称之为复数.(2)复数的表示:复数通常用字母z表示,即z =a+bi(a,b∈R).a + b i (a,b∈R)叫做复数z的代数形式. 实部虚部复数的有关概念你能列举一些复数吗?复数的有关概念(3)复数的分类:对于复数z=a+bi(a,b ∈R):◆当b=0时,复数z=a,此时它就是实数.◆当b≠0时,复数z=a+bi,此时称之为虚数.特别地,当a=0且b≠0时,复数z=bi,此时称之为纯虚数.(4)复数集:全体复数所组成的集合,叫做复数集,记作C.复数集C与前面的数集之间的关系如何?例1说出刚才所列举复数的实部与虚部,变式判断下列说法是否正确:(1)复数 iπ 的实部为0,虚部是 iπ.(2)复数 i lg1 是纯虚数.(3)复数2+(1+i)i的实部是2,虚部是(1+i).反思(1)复数z=a+bi(a,b∈R)的虚部仅指单独的实数b,不能
含有i.(2)复数的实部与虚部必须是实数.应用与反思 并指出哪些是实数,
哪些是虚数,哪些是纯虚数?例2实数m取什么值时,复数z=m(m-1)+(m-1)i是:
(1)实数? (2)虚数? (3)纯虚数?变式(4)当实数m取什么值时,复数z=0?反思复数z=a+bi(a,b∈R)是纯虚数a=0两个复数相等,当且仅当它们的实部和虚部分别相等,即a+bi = c+di(a,b,c,d∈R).应用与反思??例3已知(x+y)+(x-2y)i =(2x-5)+(3x+y)i,求实数x,y的值.反思(2)一个复数方程可裂变为两个实数方程,因而可求两
个未知数.(1)解决复数问题的基本思想:应用与反思 复数问题实数化.复数的有关概念善于抓主要矛盾复数系的扩充同样遵循复数系还需要扩充吗?知识与启迪
