5.4.2正弦函数、余弦函数的性质 课件(共20张PPT)
文档属性
| 名称 | 5.4.2正弦函数、余弦函数的性质 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 990.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 09:50:36 | ||
图片预览








文档简介
(共20张PPT)
5.4.2 正弦函数、
余弦函数的性质
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
复习引入
由正弦函数y=sinx和余弦函数y=cosx的作图过程以及正弦函数和余弦函数的定义,容易得出正弦函数y=sinx和余弦函数y=cosx有以下重要性质.
(1)定义域:
正弦函数y=sinx的定义域是实数集R
[或(-∞,+∞)],记作:y=sinx,x∈R.
余弦函数y=cosx的定义域是实数集R
[或(-∞,+∞)],记作:y=cosx,x∈R.
学习新知
我们已经学过函数,并掌握了讨论一个函数性质的几个角度,你还记得有哪些吗?在上一次课中,我们已经学习了正弦函数的y=sinx在R上图像,下面请同学们根据图像一起讨论一下它具有哪些性质?
新课引入
正弦函数y=sinx,x∈R
①当且仅当x= +2kπ,k∈Z时,正弦函数取得最大值1;
②当且仅当x=- +2kπ,k∈Z时,正弦函数取得最小值-1
(2)值域:因为正弦线的长度小于或等于单位圆的半径的长度;从正弦曲线可以看出,正弦曲线分布在两条平行线y=1和y=-1之间,所以
|sinx|≤1,即-1≤sinx≤1,
也就是说,正弦函数的值域是[-1,1].
同理余弦函数的值域是[-1,1]
学习新知
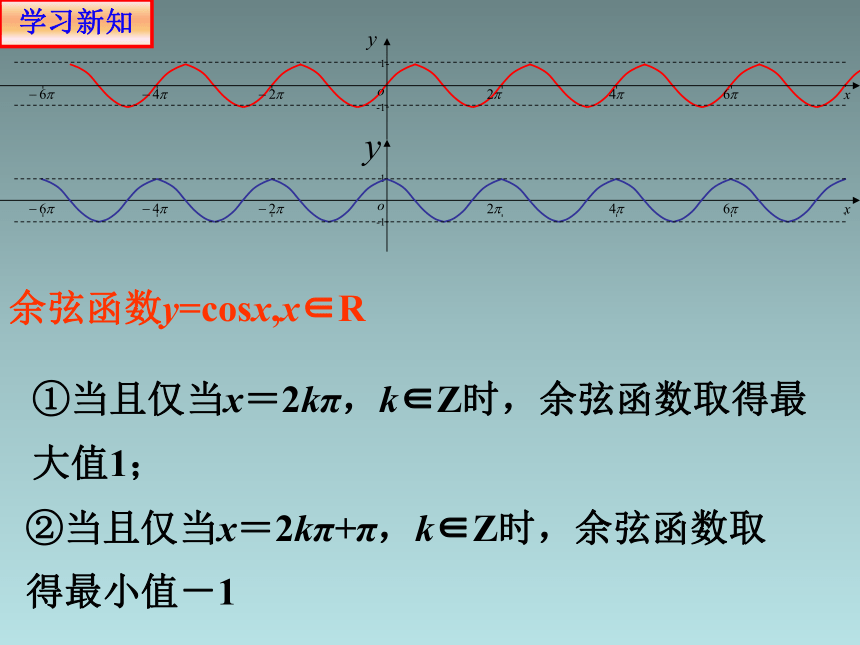
余弦函数y=cosx,x∈R
①当且仅当x=2kπ,k∈Z时,余弦函数取得最大值1;
②当且仅当x=2kπ+π,k∈Z时,余弦函数取得最小值-1
-
-
-
-
-
-
-
-
-
1
-1
-
-
-
-
-
-
-
-
-
1
-1
学习新知
(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?
在数学当中,有没有周期现象?
学习新知
(1) 正弦函数的图象是有规律不断重复出现的;
(2) 规律是:每隔2 重复出现一次(或者说每隔2k ,k Z重复出现);
(3) 这个规律由诱导公式sin(2k +x)=sinx可以说明.
正弦函数的性质1——周期性
结论:象这样一种函数叫做周期函数.
学习新知
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D,都有x+T∈D 且f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期
由此可知,2π,4π,……,-2π,-4π,
……2kπ (k∈Z且k≠0)都是正弦函数和余弦函数的周期,最小正周期是2π.
周期函数定义:
学习新知
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的最小正周期。
注意: (1) 周期函数中,x 定义域M,则必有x+T M, 且若T>0,则定义域无上界;T<0则定义域无下界;
(2) “每一个值”,只要有一个反例,则f (x)就不为周期函数(如f (x0+T) f (x0));
(3) T往往是多值的(如y=sinx, T=2 , 4 , … , -2 , - 4 , …都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期).
学习新知
学习新知
想一想
求下列函数的周期
解:(1)∵cos(x+2π)=cosx,
∴3cos(x+2π)=3cosx
∴函数y= 3cosx,x∈R的周期为2π
(2)设函数y=sin2x, x∈R的周期为T,则
sin2(x+T)=sin(2x+2T)=sin2x
∵正弦函数的最小正周期为2π ,
∴ y=sin2x ,x∈R的周期为π
典型例题
例:求下列函数的周期
解:设函数 的周期为T,则
∵正弦函数的最小正周期为2π ,
∴
∴函数 的周期为4π
典型例题
求下列三角函数的周期:
y=sin(x+ ); (2) y=3sin( + )
解: (1) 令z= x+ 而 sin(2 +z)=sinz
即:f (2 +z)=f (z) ,
f [(x+2 )+ ]=f (x+ )
∴函数的周期T=2 .
巩固练习
(2)解:令z= , 则
f (x)=3sinz=3sin(z+2 )
∴函数的周期T=4 .
=f (x+4 )
=3sin( )
=3sin( +2 )
一般结论:
学习新知
(3) y=|sinx|
解:f(x+π)=|sin(x+π)|=|sinx|,
所以函数的周期是T=π.
求下列三角函数的周期:
深化练习
正弦、余弦函数的性质2——奇偶性
请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么?
学习新知
是奇函数
是偶函数
例2.判断下列函数的奇偶性
典型例题
奇函数
非奇非偶函数
非奇非偶函数
(1)函数y=sinx的图象还有其他对称中心吗
(2)函数y=sinx的图象是轴对称图形吗?
学习新知
(3)函数y=cosx的图象还有其他对称轴吗?
(4) 函数y=cosx的图象是中心对称图形吗
定义域
值域
最大值
最小值
奇偶性
周期性
y=sinx
y=cosx
函数
性质
R
R
[-1,1]
[-1,1]
仅当
时取得最大值1
仅当
时取得最大值1
仅当
时取得最小值-1
仅当
时取得最小值-1
奇函数
偶函数
2π
2π
课堂小结
5.4.2 正弦函数、
余弦函数的性质
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
复习引入
由正弦函数y=sinx和余弦函数y=cosx的作图过程以及正弦函数和余弦函数的定义,容易得出正弦函数y=sinx和余弦函数y=cosx有以下重要性质.
(1)定义域:
正弦函数y=sinx的定义域是实数集R
[或(-∞,+∞)],记作:y=sinx,x∈R.
余弦函数y=cosx的定义域是实数集R
[或(-∞,+∞)],记作:y=cosx,x∈R.
学习新知
我们已经学过函数,并掌握了讨论一个函数性质的几个角度,你还记得有哪些吗?在上一次课中,我们已经学习了正弦函数的y=sinx在R上图像,下面请同学们根据图像一起讨论一下它具有哪些性质?
新课引入
正弦函数y=sinx,x∈R
①当且仅当x= +2kπ,k∈Z时,正弦函数取得最大值1;
②当且仅当x=- +2kπ,k∈Z时,正弦函数取得最小值-1
(2)值域:因为正弦线的长度小于或等于单位圆的半径的长度;从正弦曲线可以看出,正弦曲线分布在两条平行线y=1和y=-1之间,所以
|sinx|≤1,即-1≤sinx≤1,
也就是说,正弦函数的值域是[-1,1].
同理余弦函数的值域是[-1,1]
学习新知
余弦函数y=cosx,x∈R
①当且仅当x=2kπ,k∈Z时,余弦函数取得最大值1;
②当且仅当x=2kπ+π,k∈Z时,余弦函数取得最小值-1
-
-
-
-
-
-
-
-
-
1
-1
-
-
-
-
-
-
-
-
-
1
-1
学习新知
(1)今天是星期一,则过了七天是星期几?
过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点
运动的规律如何呢?
在数学当中,有没有周期现象?
学习新知
(1) 正弦函数的图象是有规律不断重复出现的;
(2) 规律是:每隔2 重复出现一次(或者说每隔2k ,k Z重复出现);
(3) 这个规律由诱导公式sin(2k +x)=sinx可以说明.
正弦函数的性质1——周期性
结论:象这样一种函数叫做周期函数.
学习新知
一般地,设函数f(x)的定义域为D,如果存在一个非零常数T,使得对每一个x∈D,都有x+T∈D 且f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期
由此可知,2π,4π,……,-2π,-4π,
……2kπ (k∈Z且k≠0)都是正弦函数和余弦函数的周期,最小正周期是2π.
周期函数定义:
学习新知
对于一个周期函数f(x),如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做 f(x)的最小正周期。
注意: (1) 周期函数中,x 定义域M,则必有x+T M, 且若T>0,则定义域无上界;T<0则定义域无下界;
(2) “每一个值”,只要有一个反例,则f (x)就不为周期函数(如f (x0+T) f (x0));
(3) T往往是多值的(如y=sinx, T=2 , 4 , … , -2 , - 4 , …都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期).
学习新知
学习新知
想一想
求下列函数的周期
解:(1)∵cos(x+2π)=cosx,
∴3cos(x+2π)=3cosx
∴函数y= 3cosx,x∈R的周期为2π
(2)设函数y=sin2x, x∈R的周期为T,则
sin2(x+T)=sin(2x+2T)=sin2x
∵正弦函数的最小正周期为2π ,
∴ y=sin2x ,x∈R的周期为π
典型例题
例:求下列函数的周期
解:设函数 的周期为T,则
∵正弦函数的最小正周期为2π ,
∴
∴函数 的周期为4π
典型例题
求下列三角函数的周期:
y=sin(x+ ); (2) y=3sin( + )
解: (1) 令z= x+ 而 sin(2 +z)=sinz
即:f (2 +z)=f (z) ,
f [(x+2 )+ ]=f (x+ )
∴函数的周期T=2 .
巩固练习
(2)解:令z= , 则
f (x)=3sinz=3sin(z+2 )
∴函数的周期T=4 .
=f (x+4 )
=3sin( )
=3sin( +2 )
一般结论:
学习新知
(3) y=|sinx|
解:f(x+π)=|sin(x+π)|=|sinx|,
所以函数的周期是T=π.
求下列三角函数的周期:
深化练习
正弦、余弦函数的性质2——奇偶性
请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么?
学习新知
是奇函数
是偶函数
例2.判断下列函数的奇偶性
典型例题
奇函数
非奇非偶函数
非奇非偶函数
(1)函数y=sinx的图象还有其他对称中心吗
(2)函数y=sinx的图象是轴对称图形吗?
学习新知
(3)函数y=cosx的图象还有其他对称轴吗?
(4) 函数y=cosx的图象是中心对称图形吗
定义域
值域
最大值
最小值
奇偶性
周期性
y=sinx
y=cosx
函数
性质
R
R
[-1,1]
[-1,1]
仅当
时取得最大值1
仅当
时取得最大值1
仅当
时取得最小值-1
仅当
时取得最小值-1
奇函数
偶函数
2π
2π
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
