5.6.2 函数y=Asin(ωx+φ)的图象 课件(共24张PPT)
文档属性
| 名称 | 5.6.2 函数y=Asin(ωx+φ)的图象 课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 09:53:58 | ||
图片预览





文档简介
(共24张PPT)
5.6.2正弦型函数y=Asin(ωx+φ) 的图象
四、三角函数的图象和性质
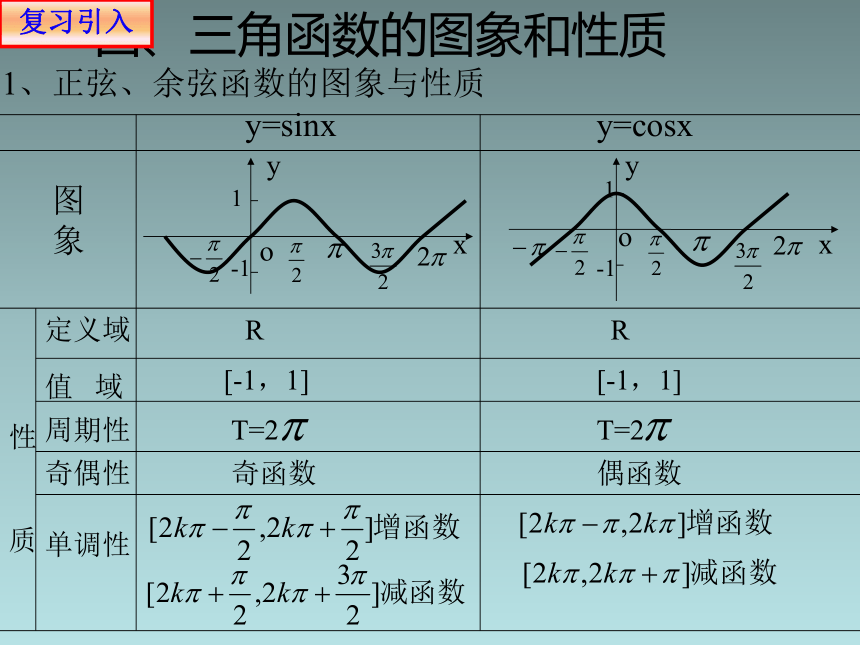
图象
y=sinx
y=cosx
x
o
y
-1
1
x
y
-1
1
性
质
定义域
R
R
值 域
[-1,1]
[-1,1]
周期性
T=2
T=2
奇偶性
奇函数
偶函数
单调性
o
1、正弦、余弦函数的图象与性质
复习引入
复习引入
C
C
复习练习
求三角函数的解析式
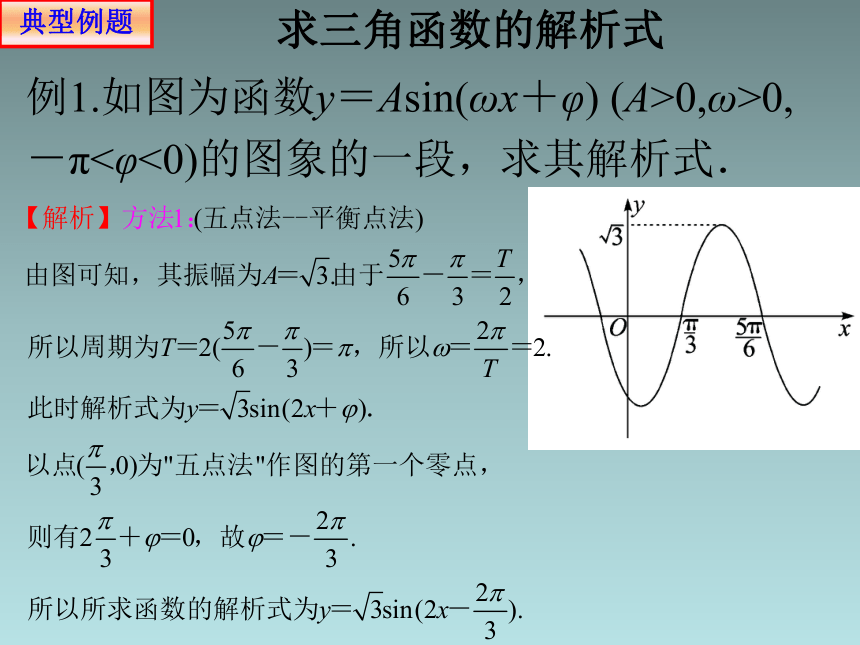
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
典型例题
典型例题
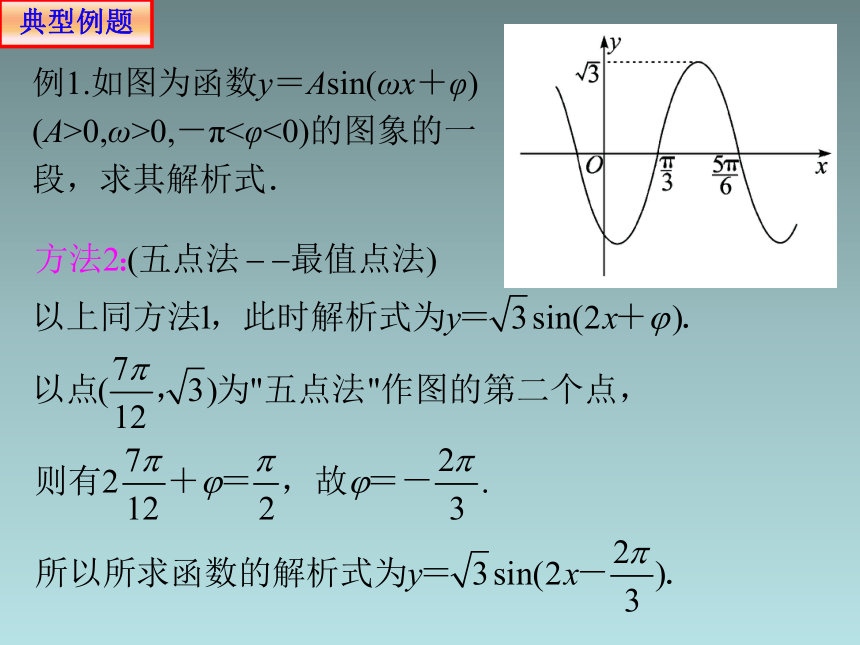
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
典型例题
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
本题由图象观察出最值与周期,就可求出A与ω,再由图象过某点,运用待定系数法求出φ.其中找最高点或最低点比较简便.
已知函数y=Asin(ωx+φ)的图象求其解析式,一般情况下,A与ω易分别根据振幅与周期求出,难点在于求φ.求A、ω、φ的本质是待定系数法.基本方法有:(1)五点法,包括平衡点法与最值点法.在运用平衡点法时,要特别注意分清是第几个平衡点.
(2)变换法,即通过弄清已知图象是由哪个图象变换得到而求出待定系数.
方法小结
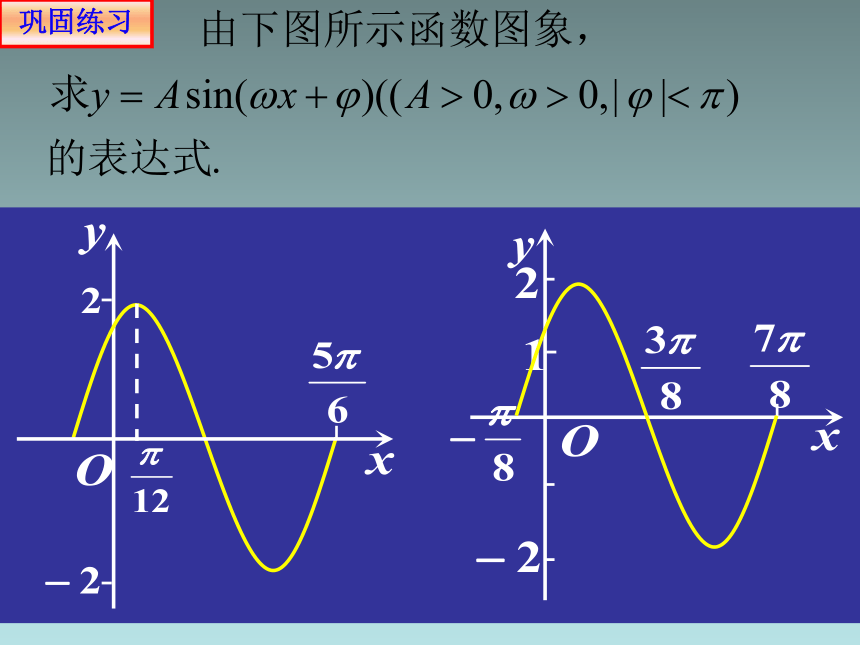
巩固练习
例2.
典型例题
(2) 代点法.
(1) 平移法;
A由图象的振幅决定;
由图象的周期决定;
求 常用的两种方法:
练习. 函数f(x)=Asin(ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,则f(0)的值是________.
方法小结
典型例题
典型例题
典型例题
1.函数f(x)=Asin (ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,则f(0)的值是________.
巩固练习
2. 已知函数y=sin(ωx+φ),在同一周期内,当x= 时函数取得最大值1,当x= 时函数取得最小值-1,则该函数的解析式为( )
A. y=sin(3x- ) B. y=sin(3x+ )
C. y=sin( + ) D. y=sin( - )
B
巩固练习
3.函数y=sin(2x+θ)的图象关于y轴对称,则θ= ( )
(A) 2kπ+ (k∈Z) (B) 2kπ+π(k∈Z) (C) kπ+ (k∈Z) (D) kπ+π(k∈Z)
C
巩固练习
4.函数y=sin(2x-5)的对称中心的坐标为 ;
( , 0) ( k∈Z)
5.函数y=2sin(2x+ )(x∈[-π,0])的单调递减区间是 ;
巩固练习
1.判断正误
①y=Asinωx的最大值是A,最小值是 -A.( )
②y=Asinωx的周期是. ( )
③y=-3sin4x的振幅是3,最大值为3,最小值是-3.( )
2.用图象变换的方法在同一坐标系内由y=sinx的图象画出函数y=-sin(-2x)的图象.
巩固练习
3.下列变换中,正确的是
A.将y=sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到y=sin x的图象
B.将y=sin2x图象上的横坐标变为原来的 倍,纵坐标变为原来的相反数,即得到y=sinx的图象
C.将y=-sin2x图象上的横坐标变为原来的 倍,且变为相反数,即得到y=sinx的图象
D.将y=-3sin2x图象上的横坐标缩小一倍,纵坐标扩大到原来的 倍(纵坐标不变)即可得到y=sinx的图象
巩固练习
巩固练习
课本第241页练习
巩固练习
课本第241页练习
巩固练习
课本第241页练习
通过本节学习,要理解并学会对函数y=sinx进行振幅和周期变换,即会画y=Asinx,y=sinωx的图象,并理解它们与y=sinx之间的关系.
能利用函数图象求函数解析式
课堂小结
(2) 代点法.
(1) 平移法;
A由图象的振幅决定;
由图象的周期决定;
求 常用的两种方法:
5.6.2正弦型函数y=Asin(ωx+φ) 的图象
四、三角函数的图象和性质
图象
y=sinx
y=cosx
x
o
y
-1
1
x
y
-1
1
性
质
定义域
R
R
值 域
[-1,1]
[-1,1]
周期性
T=2
T=2
奇偶性
奇函数
偶函数
单调性
o
1、正弦、余弦函数的图象与性质
复习引入
复习引入
C
C
复习练习
求三角函数的解析式
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
典型例题
典型例题
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
典型例题
例1.如图为函数y=Asin(ωx+φ) (A>0,ω>0,-π<φ<0)的图象的一段,求其解析式.
本题由图象观察出最值与周期,就可求出A与ω,再由图象过某点,运用待定系数法求出φ.其中找最高点或最低点比较简便.
已知函数y=Asin(ωx+φ)的图象求其解析式,一般情况下,A与ω易分别根据振幅与周期求出,难点在于求φ.求A、ω、φ的本质是待定系数法.基本方法有:(1)五点法,包括平衡点法与最值点法.在运用平衡点法时,要特别注意分清是第几个平衡点.
(2)变换法,即通过弄清已知图象是由哪个图象变换得到而求出待定系数.
方法小结
巩固练习
例2.
典型例题
(2) 代点法.
(1) 平移法;
A由图象的振幅决定;
由图象的周期决定;
求 常用的两种方法:
练习. 函数f(x)=Asin(ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,则f(0)的值是________.
方法小结
典型例题
典型例题
典型例题
1.函数f(x)=Asin (ωx+φ)
(A,ω,φ为常数,A>0,ω>0)
的部分图象如图所示,则f(0)的值是________.
巩固练习
2. 已知函数y=sin(ωx+φ),在同一周期内,当x= 时函数取得最大值1,当x= 时函数取得最小值-1,则该函数的解析式为( )
A. y=sin(3x- ) B. y=sin(3x+ )
C. y=sin( + ) D. y=sin( - )
B
巩固练习
3.函数y=sin(2x+θ)的图象关于y轴对称,则θ= ( )
(A) 2kπ+ (k∈Z) (B) 2kπ+π(k∈Z) (C) kπ+ (k∈Z) (D) kπ+π(k∈Z)
C
巩固练习
4.函数y=sin(2x-5)的对称中心的坐标为 ;
( , 0) ( k∈Z)
5.函数y=2sin(2x+ )(x∈[-π,0])的单调递减区间是 ;
巩固练习
1.判断正误
①y=Asinωx的最大值是A,最小值是 -A.( )
②y=Asinωx的周期是. ( )
③y=-3sin4x的振幅是3,最大值为3,最小值是-3.( )
2.用图象变换的方法在同一坐标系内由y=sinx的图象画出函数y=-sin(-2x)的图象.
巩固练习
3.下列变换中,正确的是
A.将y=sin2x图象上的横坐标变为原来的2倍(纵坐标不变)即可得到y=sin x的图象
B.将y=sin2x图象上的横坐标变为原来的 倍,纵坐标变为原来的相反数,即得到y=sinx的图象
C.将y=-sin2x图象上的横坐标变为原来的 倍,且变为相反数,即得到y=sinx的图象
D.将y=-3sin2x图象上的横坐标缩小一倍,纵坐标扩大到原来的 倍(纵坐标不变)即可得到y=sinx的图象
巩固练习
巩固练习
课本第241页练习
巩固练习
课本第241页练习
巩固练习
课本第241页练习
通过本节学习,要理解并学会对函数y=sinx进行振幅和周期变换,即会画y=Asinx,y=sinωx的图象,并理解它们与y=sinx之间的关系.
能利用函数图象求函数解析式
课堂小结
(2) 代点法.
(1) 平移法;
A由图象的振幅决定;
由图象的周期决定;
求 常用的两种方法:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
