数学高中苏教版选修(2-2)1.4《导数在实际生活中的应用》课件
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.4《导数在实际生活中的应用》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 154.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-03 00:00:00 | ||
图片预览






文档简介
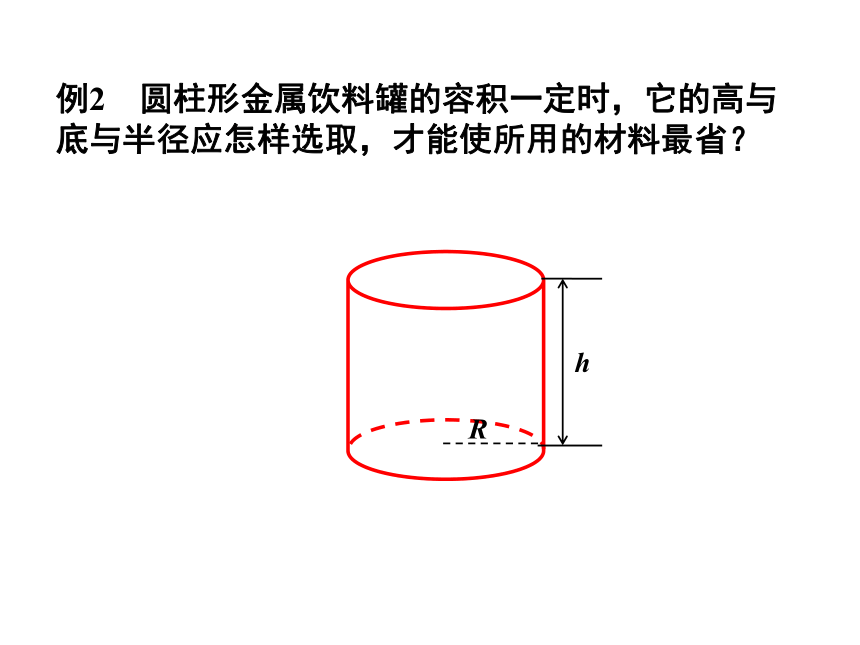
课件16张PPT。高中数学 选修2-21.4 导数在实际生活中的应用新课引入 导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以求出实际生活中的某些最值问题.1.几何方面的应用.2.物理方面的应用.3.经济学方面的应用.(面积和体积等的最值)(利润方面最值)(功和功率等最值)例1 在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?解:设箱底边长为x cm, 箱子容积为V=x2 h则箱高V ′=60x-3x2/2令V ′=0,得x=40,x=0(舍去)得V (40)=16000答:当箱底边长为x=40时,箱子容积最大,最大值为16000cm3.当x∈(0,40)时V ′(x)>0;当x∈(40,60)时V ′(x)<0;∴V (40)为极大值,且为最大值.例2 圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?解:设桶底面半径为R,因为S(R)只有一个极值,所以它是最小值.答:当罐高与底的直径相等时,所用材料最省.3变式:当圆柱形金属饮料罐的表面积为定值
S 时,它的高与底面半径应怎样选取,
才能使所用材料最省?提示:S=2πRh+2πR2 h=V(R)= πR2= (S-2πR2)R= SR-πR3V ′(R)=0 S=6πR2 6πR2= 2πRh+2πR2 h=2R.例3 在如图所示的电路中,已知电源的内阻为r,电动势为E,外电阻R为多大时,才能使电功率最大?最大电功率是多少?解:电功率P=I2R,其中I= 为电流强度,则 P=[E/(R+r)]2R=
由P′=0,解得:R=r.
列表分析,
当R=r时,P取得极大值,且是最大值.最大值为
P= .
答:当外电阻R等于内电阻r时,电功率最大,最大
电功率是 .
例4 强度分别为a,b的两个点光源A,B,它们间的距离为d,试问在连接这两个光源的线段AB上,何处照度最小?试就a=8,b=1,d=3时回答上述问题(照度与光的强度成正比,与光源距离的平方成反比.解:如图,设点P在线段AB上,且P距光源A为x,
则P距光源B为3-x(0<x<3).P点受A光源的照度为(其中,k为比例常数)P点受B光源的照度为从而,P点的总照度为:解得x=2,故当0<x<2时,I′(x)<0;当2<x<3时, I′(x)>0.因此,x=2时,I取得极小值,且是最小值.答:在连结两光源的线段AB上,距光源A为2处的照度最小.例5 在经济学中,生产x单位产品的成本称为成
本函数,记为C(x);出售x单位产品的收益称为收
益函数,记为R(x); R(x)-C(x)称为利润函数,
记为P(x).
(1)设C(x)=10-6x3-0.003x2+5x+1000,生产多
少单位产品时,边际成本C ′(x)最低?
(2)设C(x)=50x+10000,产品的单价p=100-0.01x,怎样定价可使利润最大?解:(1)c′(x)=3×10-6x2-0.006x+5=g(x),
g′(x) =6×10-6x-0.006=0,
解得:x=1000,而g(x)在x>0上仅有一个极小值,故x=1000时边际成本最低.(2)P(x)= R(x) - C(x) =x(100-0.01x)-(50x+10000)
= -0.01x2+50x- 10000 ,
x=2500,而P(x)最大,此时P=100-25=75.答:生产1000个单位产品时,边际成本最低;当生产的单价为75时,利润最大.四、课堂练习
1.将正数a分成两部分,使其立方和为最小,这两部分应分成________和________.
2.在半径为R的圆内,作内接等腰三角形,当底边上高为____时,它的面积最大.
3.有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,问剪去的小正方形边长应为多少?
4.一条水渠,断面为等腰梯形,如图所示,在确定断面尺寸时,希望在断面ABCD的面积为定值S时,使得湿周l=AB+BC+CD最小,这样可使水流阻力小,渗透少,求此时的高h和下底边长b.
?
?
?
五、回顾反思
(1)解有关函数最大值、最小值的实际问题,需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;所得结果要符合问题的实际意义.
(2)根据问题的实际意义来判断函数最值时,如果函数在此区间上只有一个极值点,那么这个极值就是所求最值,不必再与端点值比较.
(3)相当多有关最值的实际问题用导数方法解决较简单 .
S 时,它的高与底面半径应怎样选取,
才能使所用材料最省?提示:S=2πRh+2πR2 h=V(R)= πR2= (S-2πR2)R= SR-πR3V ′(R)=0 S=6πR2 6πR2= 2πRh+2πR2 h=2R.例3 在如图所示的电路中,已知电源的内阻为r,电动势为E,外电阻R为多大时,才能使电功率最大?最大电功率是多少?解:电功率P=I2R,其中I= 为电流强度,则 P=[E/(R+r)]2R=
由P′=0,解得:R=r.
列表分析,
当R=r时,P取得极大值,且是最大值.最大值为
P= .
答:当外电阻R等于内电阻r时,电功率最大,最大
电功率是 .
例4 强度分别为a,b的两个点光源A,B,它们间的距离为d,试问在连接这两个光源的线段AB上,何处照度最小?试就a=8,b=1,d=3时回答上述问题(照度与光的强度成正比,与光源距离的平方成反比.解:如图,设点P在线段AB上,且P距光源A为x,
则P距光源B为3-x(0<x<3).P点受A光源的照度为(其中,k为比例常数)P点受B光源的照度为从而,P点的总照度为:解得x=2,故当0<x<2时,I′(x)<0;当2<x<3时, I′(x)>0.因此,x=2时,I取得极小值,且是最小值.答:在连结两光源的线段AB上,距光源A为2处的照度最小.例5 在经济学中,生产x单位产品的成本称为成
本函数,记为C(x);出售x单位产品的收益称为收
益函数,记为R(x); R(x)-C(x)称为利润函数,
记为P(x).
(1)设C(x)=10-6x3-0.003x2+5x+1000,生产多
少单位产品时,边际成本C ′(x)最低?
(2)设C(x)=50x+10000,产品的单价p=100-0.01x,怎样定价可使利润最大?解:(1)c′(x)=3×10-6x2-0.006x+5=g(x),
g′(x) =6×10-6x-0.006=0,
解得:x=1000,而g(x)在x>0上仅有一个极小值,故x=1000时边际成本最低.(2)P(x)= R(x) - C(x) =x(100-0.01x)-(50x+10000)
= -0.01x2+50x- 10000 ,
x=2500,而P(x)最大,此时P=100-25=75.答:生产1000个单位产品时,边际成本最低;当生产的单价为75时,利润最大.四、课堂练习
1.将正数a分成两部分,使其立方和为最小,这两部分应分成________和________.
2.在半径为R的圆内,作内接等腰三角形,当底边上高为____时,它的面积最大.
3.有一边长分别为8与5的长方形,在各角剪去相同的小正方形,把四边折起作成一个无盖小盒,要使纸盒的容积最大,问剪去的小正方形边长应为多少?
4.一条水渠,断面为等腰梯形,如图所示,在确定断面尺寸时,希望在断面ABCD的面积为定值S时,使得湿周l=AB+BC+CD最小,这样可使水流阻力小,渗透少,求此时的高h和下底边长b.
?
?
?
五、回顾反思
(1)解有关函数最大值、最小值的实际问题,需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;所得结果要符合问题的实际意义.
(2)根据问题的实际意义来判断函数最值时,如果函数在此区间上只有一个极值点,那么这个极值就是所求最值,不必再与端点值比较.
(3)相当多有关最值的实际问题用导数方法解决较简单 .
