数学高中苏教版选修(2-2)1.5《定积分》课件1
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.5《定积分》课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 78.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-03 10:00:08 | ||
图片预览






文档简介
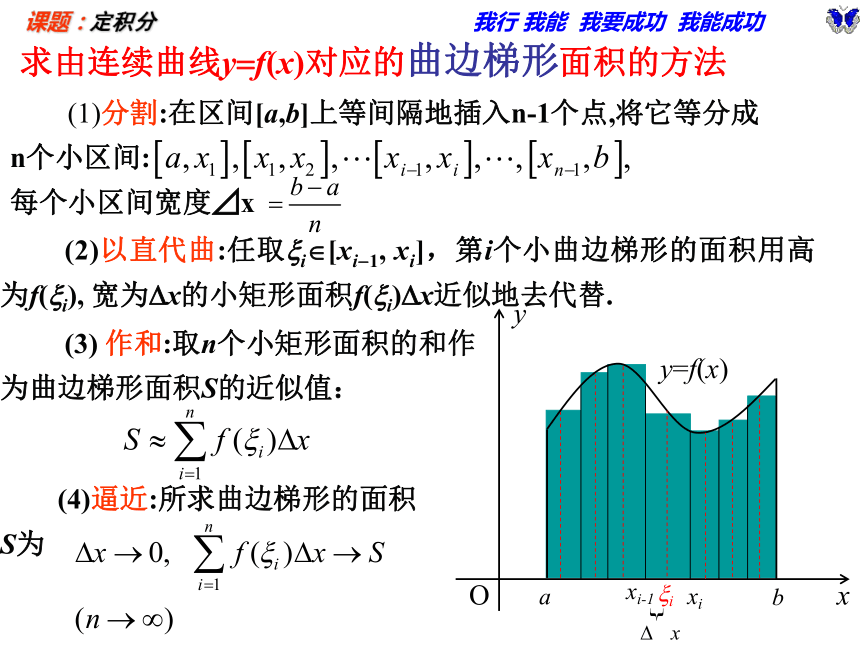
课件21张PPT。微积分在几何上主要解决两个基本问题1.如何确定曲线上一点处切线的斜率;2.如何求曲线下方“曲线梯形”的面积。直线几条线段连成的折线曲线?知识回顾:用 “以直代曲”解决问题的思想和具体操作过程:分割以直代曲作和逼近求由连续曲线y=f(x)对应的曲边梯形面积的方法 (2)以直代曲:任取xi?[xi-1, xi],第i个小曲边梯形的面积用高为f(xi), 宽为Dx的小矩形面积f(xi)Dx近似地去代替. (4)逼近:所求曲边梯形的面积S为 (3) 作和:取n个小矩形面积的和作为曲边梯形面积S的近似值:xi-1xixi (1)分割:在区间[a,b]上等间隔地插入n-1个点,将它等分成
n个小区间:
每个小区间宽度⊿x如果当n?+∞时,Sn 就无限接近于某个常数,这个常数为函数f(x)在区间[a, b]上的定积分,记作从求曲边梯形面积S的过程中可以看出,通过“四个步骤”:
分割---以直代曲----求和------逼近.定积分的定义:一般地,设函数f(x)在区间[a,b]上有定义,将区间[a,b]等分成n个小区间,每个小区的长度为 ,在每个小区间上取一点,依次为x1,x2,…….xi,….xn,作和
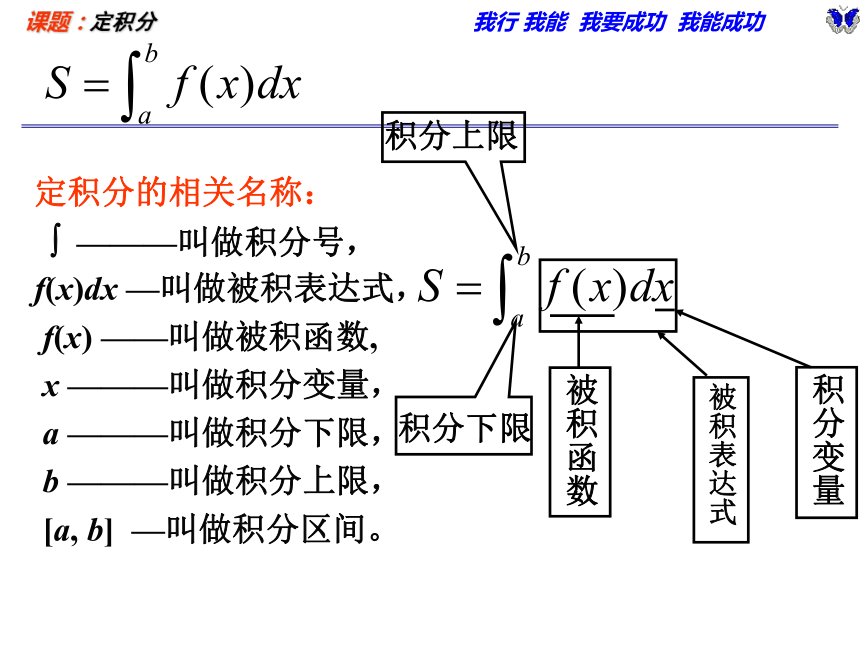
如果 无限趋近于0时,Sn无限趋近于常数S,那么称常数S为函数f(x)在区间[a,b]上的定积分,记作: .定积分的相关名称:
? ———叫做积分号,
f(x)dx —叫做被积表达式,
f(x) ——叫做被积函数,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。积分下限积分上限 按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为 (2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为 (3) 设物体在变力F=F(r)的方向上有位移,则F在位移区间[a, b]内所做的功W为注 :定积分数值只与被积函数及积分区间 [a, b] 有关, 与积分变量记号无关1.由曲线y=x2+1与直线x=1,x=3及x轴所围成的曲边梯形的面积,用定积分表示为____________.2. 中,积分上限是___,积分下限是___,积分区间是______2-2[-2,2]3.定积分 =__________.8思考: 函数在区间[a,b]上的定积分 能否为负的?定积分 定积分 =__________.定积分的几何意义. 曲线 y = f (x)
直线 x = a, x = b, y = 0 所
围成的曲边梯形的面积当函数 f (x) ? 0 , x?[a, b] 时
定积分 几何意义就是位于 x 轴下方的曲边梯形面积的相反数. 用定积分表示下列阴影部分面积 S=____;S=______;S=______;当函数 f (x)在 x?[a, b] 有正有负时, 定积分 几何意义就是图中几个曲边图形面积的代数和,(x轴上方面积取正号,x轴下方面积取负号) 定积分的几何意义: 在区间[a,b]上曲线与x轴所围成图形面积的代数和(即x轴上方的面积减去x轴下方的面积). 例:计算下列定积分.
求定积分,只要理解被积函数和定积分的意义,并作出图形,即可解决。 定积分的基本性质 性质1. 性质2. 定积分的基本性质 定积分关于积分区间具有可加性性质3. 小结:1.定积分的实质:特殊和式的逼近值.2.定积分的思想和方法:求近似以直(不变)代曲(变)取逼近3.定积分的几何意义及简单应用 1.曲边梯形面积问题;
2.变力作功问题;
3.变速运动的距离问题.我们把这些问题从具体的问题中抽象出来,作为一个数学概念提出来就是今天要讲的定积分。由此我们可以给定积分的定义……
它们都归结为:分割、近似求和、取逼近值问题情境: 课后作业:课本 P52 习题1.5
No.1、4.
n个小区间:
每个小区间宽度⊿x如果当n?+∞时,Sn 就无限接近于某个常数,这个常数为函数f(x)在区间[a, b]上的定积分,记作从求曲边梯形面积S的过程中可以看出,通过“四个步骤”:
分割---以直代曲----求和------逼近.定积分的定义:一般地,设函数f(x)在区间[a,b]上有定义,将区间[a,b]等分成n个小区间,每个小区的长度为 ,在每个小区间上取一点,依次为x1,x2,…….xi,….xn,作和
如果 无限趋近于0时,Sn无限趋近于常数S,那么称常数S为函数f(x)在区间[a,b]上的定积分,记作: .定积分的相关名称:
? ———叫做积分号,
f(x)dx —叫做被积表达式,
f(x) ——叫做被积函数,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。积分下限积分上限 按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为 (2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为 (3) 设物体在变力F=F(r)的方向上有位移,则F在位移区间[a, b]内所做的功W为注 :定积分数值只与被积函数及积分区间 [a, b] 有关, 与积分变量记号无关1.由曲线y=x2+1与直线x=1,x=3及x轴所围成的曲边梯形的面积,用定积分表示为____________.2. 中,积分上限是___,积分下限是___,积分区间是______2-2[-2,2]3.定积分 =__________.8思考: 函数在区间[a,b]上的定积分 能否为负的?定积分 定积分 =__________.定积分的几何意义. 曲线 y = f (x)
直线 x = a, x = b, y = 0 所
围成的曲边梯形的面积当函数 f (x) ? 0 , x?[a, b] 时
定积分 几何意义就是位于 x 轴下方的曲边梯形面积的相反数. 用定积分表示下列阴影部分面积 S=____;S=______;S=______;当函数 f (x)在 x?[a, b] 有正有负时, 定积分 几何意义就是图中几个曲边图形面积的代数和,(x轴上方面积取正号,x轴下方面积取负号) 定积分的几何意义: 在区间[a,b]上曲线与x轴所围成图形面积的代数和(即x轴上方的面积减去x轴下方的面积). 例:计算下列定积分.
求定积分,只要理解被积函数和定积分的意义,并作出图形,即可解决。 定积分的基本性质 性质1. 性质2. 定积分的基本性质 定积分关于积分区间具有可加性性质3. 小结:1.定积分的实质:特殊和式的逼近值.2.定积分的思想和方法:求近似以直(不变)代曲(变)取逼近3.定积分的几何意义及简单应用 1.曲边梯形面积问题;
2.变力作功问题;
3.变速运动的距离问题.我们把这些问题从具体的问题中抽象出来,作为一个数学概念提出来就是今天要讲的定积分。由此我们可以给定积分的定义……
它们都归结为:分割、近似求和、取逼近值问题情境: 课后作业:课本 P52 习题1.5
No.1、4.
