数学高中苏教版选修(2-2)1.5《定积分》课件
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.5《定积分》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 684.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-03 00:00:00 | ||
图片预览









文档简介
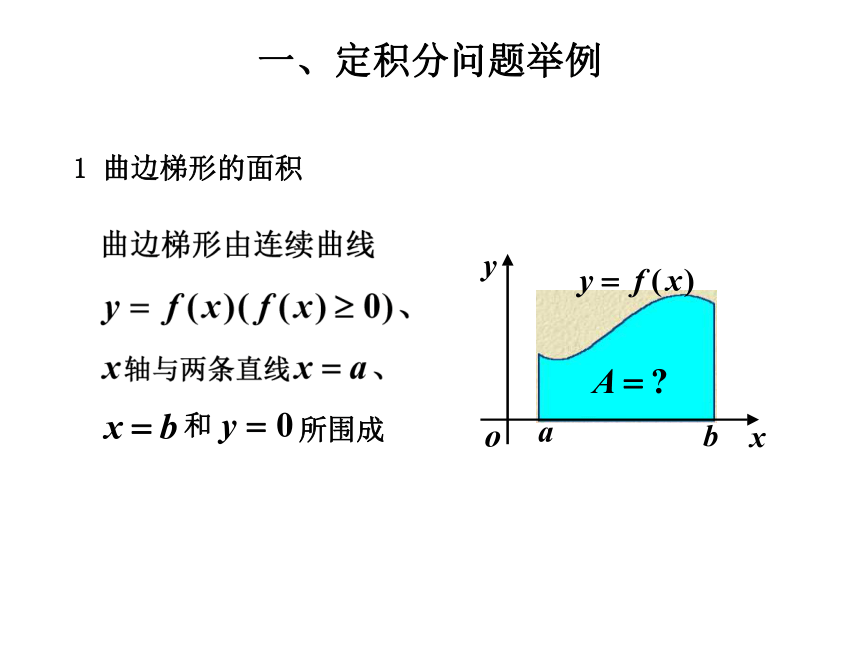
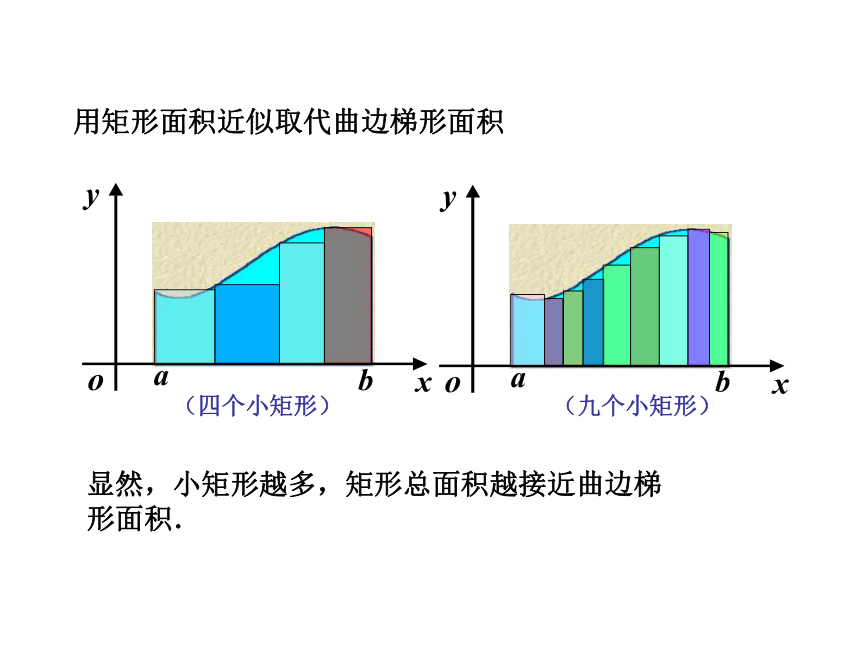
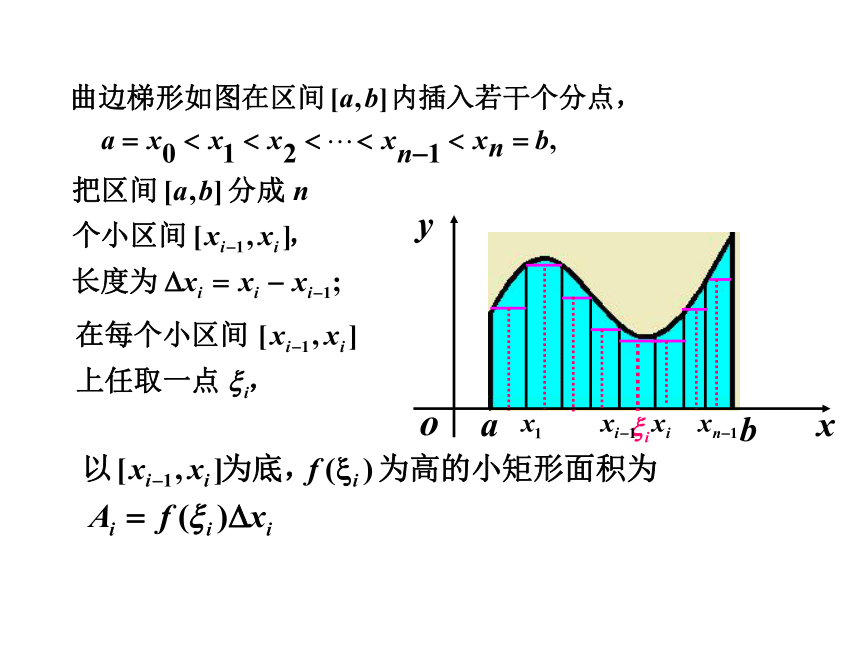
课件112张PPT。定积分定积分三、定积分的性质一、定积分问题举例二、定积分的定义1 曲边梯形的面积一、定积分问题举例用矩形面积近似取代曲边梯形面积显然,小矩形越多,矩形总面积越接近曲边梯形面积.(四个小矩形)(九个小矩形)曲边梯形如图曲边梯形面积的近似值为2 变速直线运动的路程思路:把整段时间分割成若干小段,每小段上速度看作不变,求出各小段的路程再相加,便得到路程的近似值,最后通过对时间的无限细分过程求得路程的精确值.二、定积分的定义注:存在定理定积分的几何意义几何意义:解解极限运算与对数运算换序得对定积分的补充规定:说明 在下面的性质中,假定定积分都存在,且不考虑积分上下限的大小.三、定积分的性质(此性质可以推广到有限多个函数作和的情况)(定积分对于积分区间具有可加性)性质5的推论:性质5的推论:(此性质可用于估计积分值的大致范围)由闭区间上连续函数的介值定理知积分中值公式的几何解释: 微积分基本公式 三、牛顿—莱布尼茨公式、变速直线运动中位置函数与速度
函数的联系二、积分上限函数及其导数一、变速直线运动中位置函数与速度函数的考察定积分二、积分上限函数及其导数积分上限函数的性质由积分中值定理得补充定理的重要意义:(1)肯定了连续函数的原函数是存在的.(2)初步揭示了积分学中的定积分与原函数之间的联系.三、牛顿—莱布尼茨公式微积分基本公式表明:求定积分问题转化为求原函数的问题.分析:这是 型不定式,应用洛必达法则. 定积分的换元法和分部积分法一、定积分的换元法二、定积分的分部积分法定理一、定积分的换元法应用换元公式时应注意:令定积分的分部积分公式二、定积分的分部积分法例9 证明定积分公式 定积分的应用第一节 定积分的元素法第二节 定积分在几何学上的应用第三节 定积分在物理学上的应用ab 定积分的元素法面积表示为定积分的步骤如下:(n. y提示元素法的一般步骤:这个方法通常叫做元素法.应用方向:平面图形的面积;体积;平面曲线的弧长;功;水压力;引力和平均值等. 定积分在几何学上的应用 一、平面图形的面积二、体积三、平面曲线的弧长一、平面图形的面积两曲线的交点2、极坐标系情形2a旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的立体.这直线叫做旋转轴.二、体积1 、旋转体的体积旋转体的体积为补充2、平行截面面积为已知的立体的体积如果一个立体不是旋转体,但却知道该立体上垂直于一定轴的各个截面面积,那么,这个立体的体积也可用定积分来计算.解取坐标系如图底圆方程为截面面积立体体积三、平面曲线弧长的概念曲线弧为弧长1、参数方程解星形线的参数方程为根据对称性第一象限部分的弧长证根据椭圆的对称性知故原结论成立.弧长元素弧长2、直角坐标方程解所求弧长为解曲线弧为弧长极坐标方程解解例17 计算摆线的一拱 的长度.解 弧长元素为从而,所求弧长
函数的联系二、积分上限函数及其导数一、变速直线运动中位置函数与速度函数的考察定积分二、积分上限函数及其导数积分上限函数的性质由积分中值定理得补充定理的重要意义:(1)肯定了连续函数的原函数是存在的.(2)初步揭示了积分学中的定积分与原函数之间的联系.三、牛顿—莱布尼茨公式微积分基本公式表明:求定积分问题转化为求原函数的问题.分析:这是 型不定式,应用洛必达法则. 定积分的换元法和分部积分法一、定积分的换元法二、定积分的分部积分法定理一、定积分的换元法应用换元公式时应注意:令定积分的分部积分公式二、定积分的分部积分法例9 证明定积分公式 定积分的应用第一节 定积分的元素法第二节 定积分在几何学上的应用第三节 定积分在物理学上的应用ab 定积分的元素法面积表示为定积分的步骤如下:(n. y提示元素法的一般步骤:这个方法通常叫做元素法.应用方向:平面图形的面积;体积;平面曲线的弧长;功;水压力;引力和平均值等. 定积分在几何学上的应用 一、平面图形的面积二、体积三、平面曲线的弧长一、平面图形的面积两曲线的交点2、极坐标系情形2a旋转体就是由一个平面图形饶这平面内一条直线旋转一周而成的立体.这直线叫做旋转轴.二、体积1 、旋转体的体积旋转体的体积为补充2、平行截面面积为已知的立体的体积如果一个立体不是旋转体,但却知道该立体上垂直于一定轴的各个截面面积,那么,这个立体的体积也可用定积分来计算.解取坐标系如图底圆方程为截面面积立体体积三、平面曲线弧长的概念曲线弧为弧长1、参数方程解星形线的参数方程为根据对称性第一象限部分的弧长证根据椭圆的对称性知故原结论成立.弧长元素弧长2、直角坐标方程解所求弧长为解曲线弧为弧长极坐标方程解解例17 计算摆线的一拱 的长度.解 弧长元素为从而,所求弧长
