近三年(2019-2021)高考真题数学分类汇编 专题15 不等式选讲(Word含答案)
文档属性
| 名称 | 近三年(2019-2021)高考真题数学分类汇编 专题15 不等式选讲(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 20:55:48 | ||
图片预览


文档简介
专题15 不等式选讲
1.【2020年·全国Ⅰ卷(理)】已知函数.
(1)画出的图像;
(2)求不等式的解集.
2.【2019年·全国Ⅱ卷(理)】已知
(1)当时,求不等式的解集;
(2)若时,,求的取值范围.
3.【2020年·全国Ⅲ卷(理)】设a,b,,,.
(1)证明:;
(2)用表示a,b,c的最大值,证明:.
4.【2019年·全国Ⅰ卷(理)】已知为正数,且满足.证明:
(1);
(2)
5.【2020年·全国Ⅱ卷(文)】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
6.【2019年·全国Ⅲ卷(理)】设,且.
(1)求的最小值;
(2)若成立,证明:或.
7.【2021年·全国甲卷(文)】已知函数,.
(1)画出和的图象;
(2)若,求a的取值范围.
8.【2021年·全国乙卷(理)】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
答案以及解析
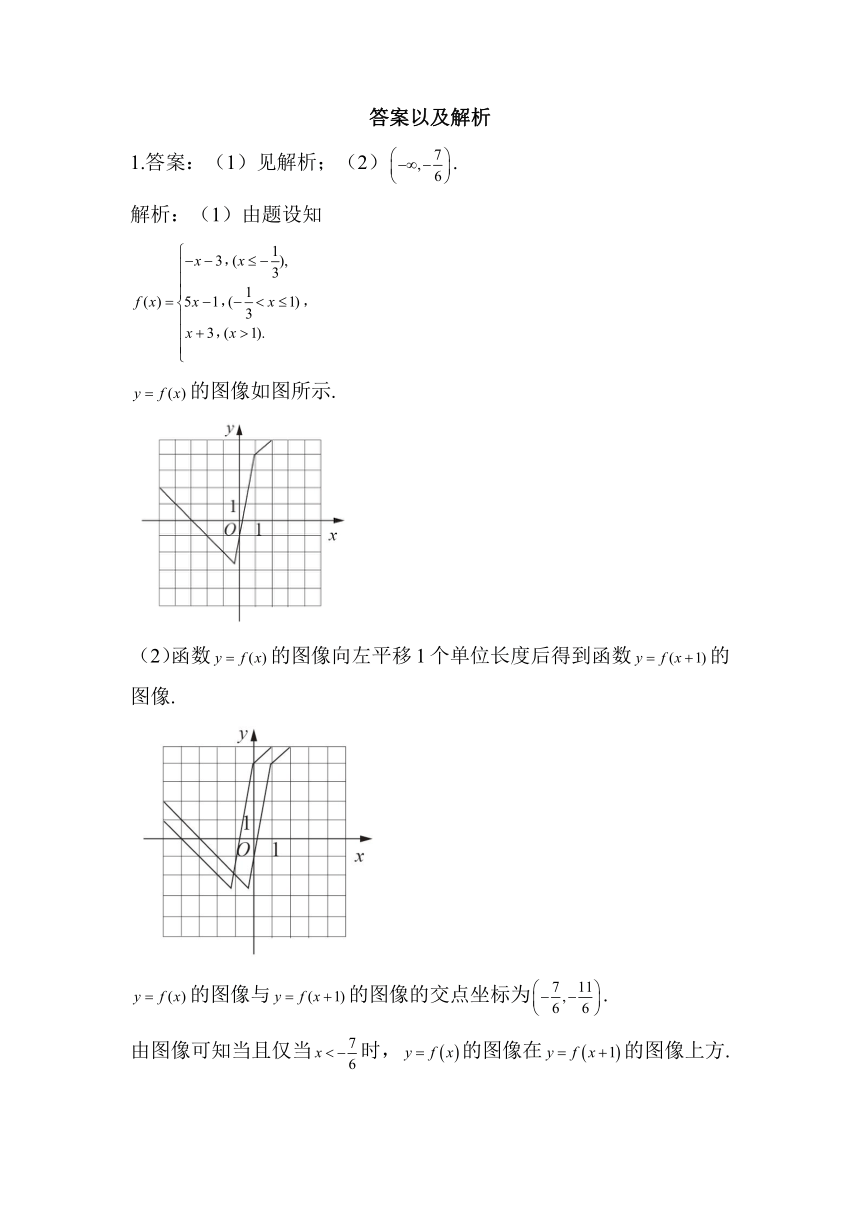
1.答案:(1)见解析;(2).
解析:(1)由题设知
的图像如图所示.
(2)函数的图像向左平移1个单位长度后得到函数的图像.
的图像与的图像的交点坐标为.
由图像可知当且仅当时,的图像在的图像上方.
故不等式的解集为.
2.答案:(1).当时,.
当时,;当时,.
所以,不等式的解集为.
(2).因为,所以.
当,时,
所以,的取值范围是.
3.答案:(1)由题设可知,均不为零,所以
.
(2)不妨设,因为,所以.由,可得,故,所以.
4.答案:(1)因为,又,故有
.
所以.
(2)因为为正数且,故有
.
所以.
5.答案:(1)当时
因此,不等式的解集为或.
(2)因为,故当,即时,.所以当或时,.
当时,.
所以a的取值范围是.
6.答案:(1)由于
,
故由已知得,
当且仅当时等号成立.
所以的最小值为.
(2)由于
,
故由已知,
当且仅当,,时等号成立.
因此的最小值为.
由题设知,解得或.
7.答案:(1)由已知得
所以与的图象为
(2)的图象是由函数的图象向左平移个单位长度或向右平移个单位长度得到的,根据图象可知向右平移不符合题意,向左平移到的图象的右支过的图象上的点时为临界状态,如图所示,此时的图象的右支对应的函数解析式为,则,解得.
因为,所以,
故a的取值范围为.
8.答案:(1)当时,
因为,所以或或
所以或,
所以不等式的解集为.
(2),
当且仅当时等号成立.
若,则,
两边平方可得,解得,
即a的取值范围是.
1.【2020年·全国Ⅰ卷(理)】已知函数.
(1)画出的图像;
(2)求不等式的解集.
2.【2019年·全国Ⅱ卷(理)】已知
(1)当时,求不等式的解集;
(2)若时,,求的取值范围.
3.【2020年·全国Ⅲ卷(理)】设a,b,,,.
(1)证明:;
(2)用表示a,b,c的最大值,证明:.
4.【2019年·全国Ⅰ卷(理)】已知为正数,且满足.证明:
(1);
(2)
5.【2020年·全国Ⅱ卷(文)】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
6.【2019年·全国Ⅲ卷(理)】设,且.
(1)求的最小值;
(2)若成立,证明:或.
7.【2021年·全国甲卷(文)】已知函数,.
(1)画出和的图象;
(2)若,求a的取值范围.
8.【2021年·全国乙卷(理)】已知函数.
(1)当时,求不等式的解集;
(2)若,求a的取值范围.
答案以及解析
1.答案:(1)见解析;(2).
解析:(1)由题设知
的图像如图所示.
(2)函数的图像向左平移1个单位长度后得到函数的图像.
的图像与的图像的交点坐标为.
由图像可知当且仅当时,的图像在的图像上方.
故不等式的解集为.
2.答案:(1).当时,.
当时,;当时,.
所以,不等式的解集为.
(2).因为,所以.
当,时,
所以,的取值范围是.
3.答案:(1)由题设可知,均不为零,所以
.
(2)不妨设,因为,所以.由,可得,故,所以.
4.答案:(1)因为,又,故有
.
所以.
(2)因为为正数且,故有
.
所以.
5.答案:(1)当时
因此,不等式的解集为或.
(2)因为,故当,即时,.所以当或时,.
当时,.
所以a的取值范围是.
6.答案:(1)由于
,
故由已知得,
当且仅当时等号成立.
所以的最小值为.
(2)由于
,
故由已知,
当且仅当,,时等号成立.
因此的最小值为.
由题设知,解得或.
7.答案:(1)由已知得
所以与的图象为
(2)的图象是由函数的图象向左平移个单位长度或向右平移个单位长度得到的,根据图象可知向右平移不符合题意,向左平移到的图象的右支过的图象上的点时为临界状态,如图所示,此时的图象的右支对应的函数解析式为,则,解得.
因为,所以,
故a的取值范围为.
8.答案:(1)当时,
因为,所以或或
所以或,
所以不等式的解集为.
(2),
当且仅当时等号成立.
若,则,
两边平方可得,解得,
即a的取值范围是.
同课章节目录
