人教版五年级下学期数学 分数的意义和性质 整理和复习 课件 (共67张PPT)
文档属性
| 名称 | 人教版五年级下学期数学 分数的意义和性质 整理和复习 课件 (共67张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 12:06:39 | ||
图片预览






文档简介
(共67张PPT)
整理和复习
分数的意义和性质
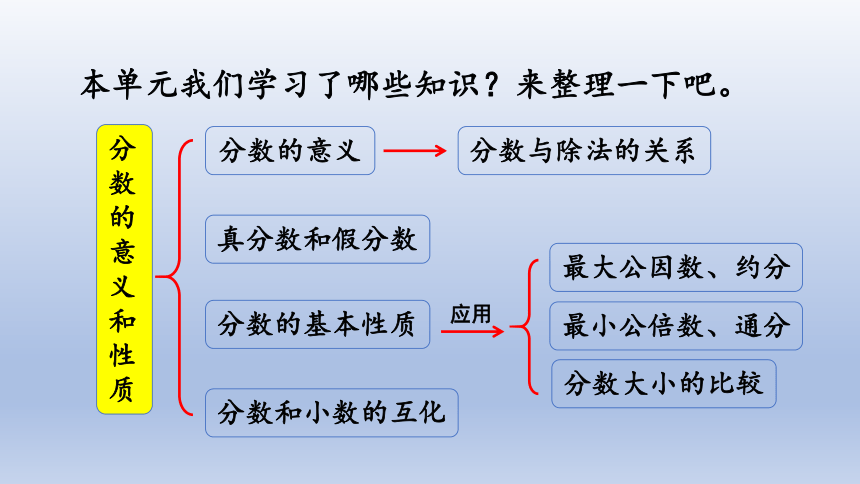
分数的意义和性质
真分数和假分数
分数的基本性质
分数的意义
分数与除法的关系
分数大小的比较
最大公因数、约分
最小公倍数、通分
分数和小数的互化
本单元我们学习了哪些知识?来整理一下吧。
应用
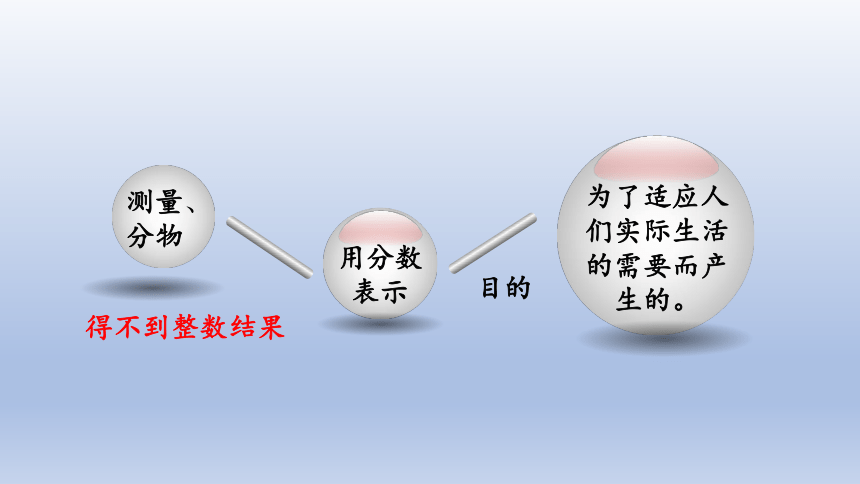
分数的产生
日常中,不能正好得到整数的结果,这时常用分数来表示。
得不到整数结果
目的
用分数表示
为了适应人们实际生活的需要而产生的。
测量、
分物
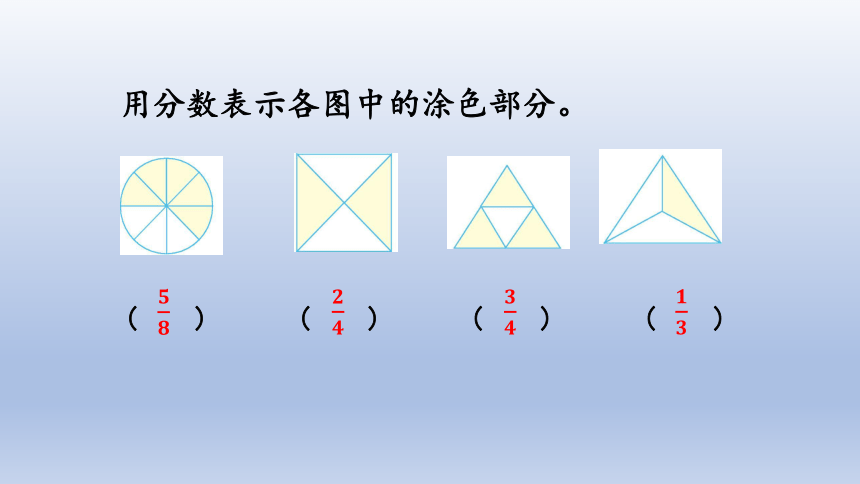
用分数表示各图中的涂色部分。
( ) ( ) ( ) ( )
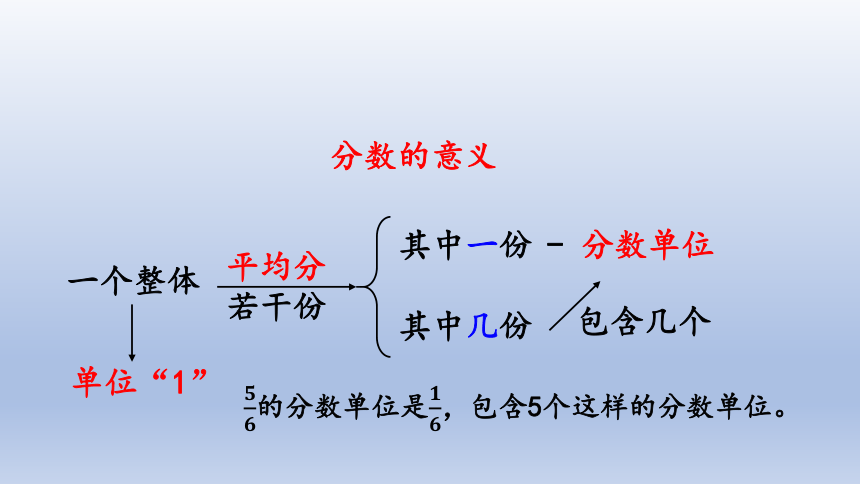
分数的意义
把单位“1”平均分成若干份,表示这样的一份或几份的数就是分数,其中表示一份的数叫分数单位。
分数的意义是什么?分数单位表示什么?
分数的意义
一个整体
平均分若干份
其中一份
其中几份
单位“1”
- 分数单位
的分数单位是,包含5个这样的分数单位。
包含几个
写出下面分数的分数单位。
一个分数的分母是几,它的分数单位就是几分之一。
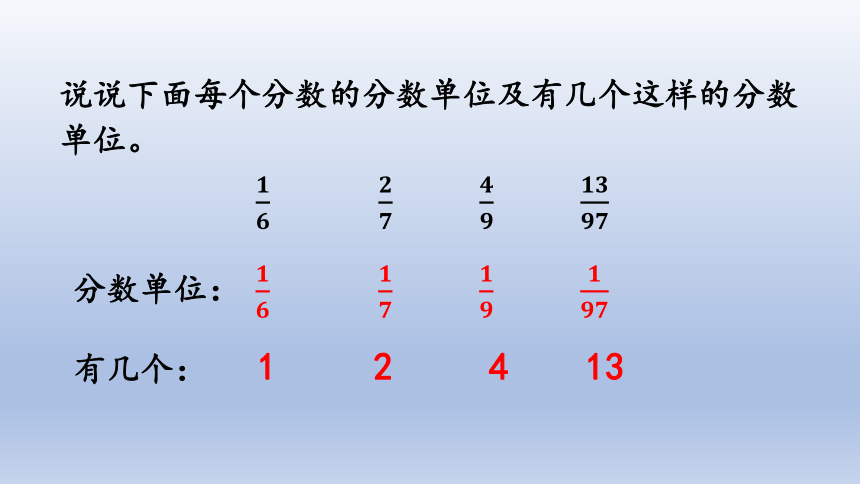
说说下面每个分数的分数单位及有几个这样的分数单位。
分数单位:
有几个:
1 2 4 13
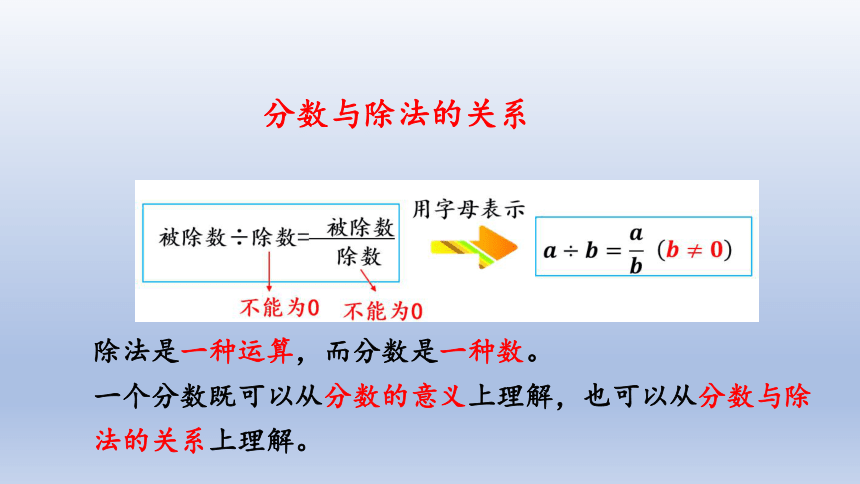
分数与除法的关系
除法是一种运算,而分数是一种数。
一个分数既可以从分数的意义上理解,也可以从分数与除法的关系上理解。
千克表示把3千克平均分成( )份,取其中的( )份,每份是( )千克;也可表示把( )千克平均分成( )份,取其中的( )份,每份是( )千克。
8
1
1
8
3
在括号里填上适当的数。
( ) ÷ ( )
( ) ÷ 27=
5 ÷ ( )=
23 ÷ 49=
13
42
4
49
13
5
23
1.用分数表示下面各算式的商。
(1)5÷9 (2)14÷17 (3)8÷15
2.米可以理解为:
把( )米平均分成( )份,表示其中的( )份;
把( )米平均分成( )份,表示其中的( )份;
=
=
=
3
5
1
1
5
3
求一个数是另一个数的几分之几
2.商是分数,表示的是两个数的倍比关系,后面不写单位。
1.先判断出单位“1”,单位“1”是除数。
五(1)班有男生28人,女生17人,女生人数是全班人数的几分之几?
28+17=45(人)
17÷45 =
答:女生人数是全班人数的。
单位“1”
甲有37张邮票,乙有16张邮票,丙有27张邮票。乙的邮票张数分别是甲和丙的几分之几
16÷37=
16÷27=
答:乙的邮票张数是甲的丙的。
真分数和假分数
真分数:分子比分母小的分数叫做真分数。
假分数:分子比分母大或者分子分母相等的分数
叫做假分数。
带分数:由整数(不包括0)和真分数合成的数叫
做带分数。
<1
≥1
说一说:真分数、假分数和带分数有什么意义与特征?
假分数 整数、带分数
分子小于分母
分数 分子与分母的大小关系 分数与1的大小关系
分数小于1
1<3
3<4
5<6
分析、比较,说说你发现了什么?
像这样分子比分母小的分数叫做真分数。
分数 分子与分母的大小关系 分数与1的大小关系
4>3
3=3
7>4
11>5
= 1
分子大于或等于分母
分数大于或等于1
像这样分子比分母大的分数叫做假分数。
观察,你发现了什么?
=
=
像这样由整数和真分数合成的数叫做带分数。
一又四分之三
二又五分之一
1读作:( ) 2读作:( )
二又五分之二写作:( )
三又八分之五写作:( )
读读写写。
一又二分之一
二又五分之一
下面的分数哪些是真分数,哪些是假分数?
真分数
假分数
分子÷分母
没有余数
有余数
假分数化成整数或带分数的方法
商-整数部分
-整数
余数-带分数的分子
分母不变
-带分数
把下面的带分数化成假分数。
2
4
2
2×3+1=7
4×5+2=22
4
把下面的假分数化成带分数或整数。
15÷2=7……1
8÷5=1……3
21÷7=3
50÷9=5……5
分数的基本性质
分数的分子分母同时乘或除以相同的数(0除外),分数的大小不变。
把、和化成分母是18而大小不变的分数。
先把分母变成18,然后看分母乘还是除以了几,分子也相应的乘或除以几即可。
在括号内填上适当的数。
== == =====
= =
5
2
10
16
4
4
4
3
3
9
28
6
2
公因数和最大公因数
几个数公有的因数,叫做这几个数的公因数;
其中最大的
一个,叫做这几个数的最大公因数。
最大公因数的求法
列举法
集合法
分解质因数法
短除法
找出两个数的公因数和最大公因数。
1.先找两个数各自的因数。
2.再找公因数。
3.找出最大的公因数。
1.先找一个数的因数。
2.从中再找出另一个数的因数。
3.找出最大的公因数。
你有不同看法吗?
8和12的公因数
1
8的因数:
2
4
8
1
12的因数:
2
3
4
6
12
1、2、4是8和12共同的因数。
的公因数。
用分解质因数法。 短除法
最大公因数及其求法
求下列各数的最大公因数。
12和36 9和10 23和46 11和17
12 36
2
6 18
6
1 3
2×6=12
23 46
23
1 2
公因数只有1的两个数叫做互质数。
12和36的最大公因数是12。
23和46的最大公因数是23。
公因数和最大公因数的应用
在铺地砖问题中,要使地面铺满且使用的地砖是整块时,就是求长和宽的公因数;要求地砖的边长最大是多少,就是求长和宽的最大公因数。
4×3=12(人)
48 36
4
12 9
3
4 3
男生:48÷12=4(排) 女生:36÷12=3(排)
男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人?这时男、女生分别有几排?
答:每排最多12人,这时男生4排,女生3排。
约分
把一个分数化成和它相等,但分子分母都比较小的分数,叫做约分。
=
最简分数
分子、分母只有公因数1的分数是最简分数。
是最简分数。
你还能再举例吗
约分的方法
可以用分子和分母的公因数依次约分,也
可以直接用分子和分母的最大公因数约分。
约分时,通常要约成最简分数。
或者
12
15
4
5
=
5
4
=
=( )÷( )=( )÷4==
18
24
3
32
9
分数与除法的关系
分数的
基本性质
把下面的分数约成最简分数。
=
=
=
=
=
把上下两行相等的两个分数用线连起来。
公倍数和最小公倍数
几个数公有的倍数,叫做这几个数的公倍数;
其中最小的
一个,叫做这几个数的最小公倍数。
最小公倍数的求法
列举法
集合法
分解质因数法
短除法
求下列每组数的最小公倍数。
4和15 1和7 4和10
1和7小公倍数
是7。
4 10
2
2 5
2×2×5=20
4×15=60
成倍数关系的两个数的最小公倍数是较大数。
两个互质数的乘积就是它们的最小公倍数。
求下列每组数的最小公倍数。
8和10 6和15 6和9
6 9
3
2 3
3×2×3=18
6 15
3
2 5
3×2×5=30
8 10
2
4 5
2×4×5=40
短除法:所有的除数和商连乘所得积,是最小公倍数。
最小公倍数的应用
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
学校组织体操队,要求队形变成10行、15行时,队形都是长方形。最少需要多少人参加体操队?
就是求10和15的最小公倍数。
10 15
5
2 3
5×2×3=30
答:最少需要30人参加体操队。
同分母分数比较大小
分母相同的两个分数,分子大的分数大。
比较下面各组分数的大小。
○ ○ ○ ○
<
<
<
>
观察这些分数,你发现了什么?
每组分母相同。
分母相同,分子大的分数大。
同分子分数比较大小
分子相同的两个分数,分母大的分数大。
再比较一下:
○ ○ ○ ○
观察这些分数,你发现了什么?
每组分子相同。
<
>
>
>
分子相同,分母大的分数小。
在○里填上“>”“<”或“=”。
○ ○ ○ ○
○ ○ ○ ○
>
<
<
<
>
=
<
>
通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分的方法
==
==
通分时用原分母的最小公倍数作公分母,然后把各分数化成以此作分母的分数。
在比较异分母分数的大小时,如果分母较大,且分数的分子较小,那么可以化成同分子分数进行比较。
=
=
>
把下面每组中的两个分数通分。
(1) =
=
(2) =
=
7
7
35
28
5
5
35
30
2
2
20
18
5
5
20
15
把下面的分数按照从小到大的顺序排列起来。
=
=
=
=
=
<<<<<
如何找到他们的最小公倍数?
小数化成分数
写成分母是10,100,1000,……的分数,再化简。
0.25
=
=
分数化成小数
=5÷14≈0.36
分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
想一想,如何判断一个数能不能化成有限小数?
分母是10,100,1000,……的分数化成小数,可以直接去掉分母,看分母1后面有几个0,就在分子中从最后一位起向左数出几位,点上小数点。
=0.7
=0.39
把小数和相等的分数用线连起来。
0.6 0.03 0.45 3.25 0.18
把下面的分数化成小数(不能化成有限小数的保留两位小数)。
=4÷9≈0.44
=7÷30≈0.23
=5÷6≈0.83
=11÷50=0.22
=0.31
=2÷25=0.8
=23÷20=1.15
做一做,并说说你是怎么想的?
○
○
○
○
<
>
<
>
用分数表示各图中的涂色部分。
8
5
4
7
5
7
在直线上描出表示下面各分数的点。
谢谢聆听
整理和复习
分数的意义和性质
分数的意义和性质
真分数和假分数
分数的基本性质
分数的意义
分数与除法的关系
分数大小的比较
最大公因数、约分
最小公倍数、通分
分数和小数的互化
本单元我们学习了哪些知识?来整理一下吧。
应用
分数的产生
日常中,不能正好得到整数的结果,这时常用分数来表示。
得不到整数结果
目的
用分数表示
为了适应人们实际生活的需要而产生的。
测量、
分物
用分数表示各图中的涂色部分。
( ) ( ) ( ) ( )
分数的意义
把单位“1”平均分成若干份,表示这样的一份或几份的数就是分数,其中表示一份的数叫分数单位。
分数的意义是什么?分数单位表示什么?
分数的意义
一个整体
平均分若干份
其中一份
其中几份
单位“1”
- 分数单位
的分数单位是,包含5个这样的分数单位。
包含几个
写出下面分数的分数单位。
一个分数的分母是几,它的分数单位就是几分之一。
说说下面每个分数的分数单位及有几个这样的分数单位。
分数单位:
有几个:
1 2 4 13
分数与除法的关系
除法是一种运算,而分数是一种数。
一个分数既可以从分数的意义上理解,也可以从分数与除法的关系上理解。
千克表示把3千克平均分成( )份,取其中的( )份,每份是( )千克;也可表示把( )千克平均分成( )份,取其中的( )份,每份是( )千克。
8
1
1
8
3
在括号里填上适当的数。
( ) ÷ ( )
( ) ÷ 27=
5 ÷ ( )=
23 ÷ 49=
13
42
4
49
13
5
23
1.用分数表示下面各算式的商。
(1)5÷9 (2)14÷17 (3)8÷15
2.米可以理解为:
把( )米平均分成( )份,表示其中的( )份;
把( )米平均分成( )份,表示其中的( )份;
=
=
=
3
5
1
1
5
3
求一个数是另一个数的几分之几
2.商是分数,表示的是两个数的倍比关系,后面不写单位。
1.先判断出单位“1”,单位“1”是除数。
五(1)班有男生28人,女生17人,女生人数是全班人数的几分之几?
28+17=45(人)
17÷45 =
答:女生人数是全班人数的。
单位“1”
甲有37张邮票,乙有16张邮票,丙有27张邮票。乙的邮票张数分别是甲和丙的几分之几
16÷37=
16÷27=
答:乙的邮票张数是甲的丙的。
真分数和假分数
真分数:分子比分母小的分数叫做真分数。
假分数:分子比分母大或者分子分母相等的分数
叫做假分数。
带分数:由整数(不包括0)和真分数合成的数叫
做带分数。
<1
≥1
说一说:真分数、假分数和带分数有什么意义与特征?
假分数 整数、带分数
分子小于分母
分数 分子与分母的大小关系 分数与1的大小关系
分数小于1
1<3
3<4
5<6
分析、比较,说说你发现了什么?
像这样分子比分母小的分数叫做真分数。
分数 分子与分母的大小关系 分数与1的大小关系
4>3
3=3
7>4
11>5
= 1
分子大于或等于分母
分数大于或等于1
像这样分子比分母大的分数叫做假分数。
观察,你发现了什么?
=
=
像这样由整数和真分数合成的数叫做带分数。
一又四分之三
二又五分之一
1读作:( ) 2读作:( )
二又五分之二写作:( )
三又八分之五写作:( )
读读写写。
一又二分之一
二又五分之一
下面的分数哪些是真分数,哪些是假分数?
真分数
假分数
分子÷分母
没有余数
有余数
假分数化成整数或带分数的方法
商-整数部分
-整数
余数-带分数的分子
分母不变
-带分数
把下面的带分数化成假分数。
2
4
2
2×3+1=7
4×5+2=22
4
把下面的假分数化成带分数或整数。
15÷2=7……1
8÷5=1……3
21÷7=3
50÷9=5……5
分数的基本性质
分数的分子分母同时乘或除以相同的数(0除外),分数的大小不变。
把、和化成分母是18而大小不变的分数。
先把分母变成18,然后看分母乘还是除以了几,分子也相应的乘或除以几即可。
在括号内填上适当的数。
== == =====
= =
5
2
10
16
4
4
4
3
3
9
28
6
2
公因数和最大公因数
几个数公有的因数,叫做这几个数的公因数;
其中最大的
一个,叫做这几个数的最大公因数。
最大公因数的求法
列举法
集合法
分解质因数法
短除法
找出两个数的公因数和最大公因数。
1.先找两个数各自的因数。
2.再找公因数。
3.找出最大的公因数。
1.先找一个数的因数。
2.从中再找出另一个数的因数。
3.找出最大的公因数。
你有不同看法吗?
8和12的公因数
1
8的因数:
2
4
8
1
12的因数:
2
3
4
6
12
1、2、4是8和12共同的因数。
的公因数。
用分解质因数法。 短除法
最大公因数及其求法
求下列各数的最大公因数。
12和36 9和10 23和46 11和17
12 36
2
6 18
6
1 3
2×6=12
23 46
23
1 2
公因数只有1的两个数叫做互质数。
12和36的最大公因数是12。
23和46的最大公因数是23。
公因数和最大公因数的应用
在铺地砖问题中,要使地面铺满且使用的地砖是整块时,就是求长和宽的公因数;要求地砖的边长最大是多少,就是求长和宽的最大公因数。
4×3=12(人)
48 36
4
12 9
3
4 3
男生:48÷12=4(排) 女生:36÷12=3(排)
男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人?这时男、女生分别有几排?
答:每排最多12人,这时男生4排,女生3排。
约分
把一个分数化成和它相等,但分子分母都比较小的分数,叫做约分。
=
最简分数
分子、分母只有公因数1的分数是最简分数。
是最简分数。
你还能再举例吗
约分的方法
可以用分子和分母的公因数依次约分,也
可以直接用分子和分母的最大公因数约分。
约分时,通常要约成最简分数。
或者
12
15
4
5
=
5
4
=
=( )÷( )=( )÷4==
18
24
3
32
9
分数与除法的关系
分数的
基本性质
把下面的分数约成最简分数。
=
=
=
=
=
把上下两行相等的两个分数用线连起来。
公倍数和最小公倍数
几个数公有的倍数,叫做这几个数的公倍数;
其中最小的
一个,叫做这几个数的最小公倍数。
最小公倍数的求法
列举法
集合法
分解质因数法
短除法
求下列每组数的最小公倍数。
4和15 1和7 4和10
1和7小公倍数
是7。
4 10
2
2 5
2×2×5=20
4×15=60
成倍数关系的两个数的最小公倍数是较大数。
两个互质数的乘积就是它们的最小公倍数。
求下列每组数的最小公倍数。
8和10 6和15 6和9
6 9
3
2 3
3×2×3=18
6 15
3
2 5
3×2×5=30
8 10
2
4 5
2×4×5=40
短除法:所有的除数和商连乘所得积,是最小公倍数。
最小公倍数的应用
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
学校组织体操队,要求队形变成10行、15行时,队形都是长方形。最少需要多少人参加体操队?
就是求10和15的最小公倍数。
10 15
5
2 3
5×2×3=30
答:最少需要30人参加体操队。
同分母分数比较大小
分母相同的两个分数,分子大的分数大。
比较下面各组分数的大小。
○ ○ ○ ○
<
<
<
>
观察这些分数,你发现了什么?
每组分母相同。
分母相同,分子大的分数大。
同分子分数比较大小
分子相同的两个分数,分母大的分数大。
再比较一下:
○ ○ ○ ○
观察这些分数,你发现了什么?
每组分子相同。
<
>
>
>
分子相同,分母大的分数小。
在○里填上“>”“<”或“=”。
○ ○ ○ ○
○ ○ ○ ○
>
<
<
<
>
=
<
>
通分
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分的方法
==
==
通分时用原分母的最小公倍数作公分母,然后把各分数化成以此作分母的分数。
在比较异分母分数的大小时,如果分母较大,且分数的分子较小,那么可以化成同分子分数进行比较。
=
=
>
把下面每组中的两个分数通分。
(1) =
=
(2) =
=
7
7
35
28
5
5
35
30
2
2
20
18
5
5
20
15
把下面的分数按照从小到大的顺序排列起来。
=
=
=
=
=
<<<<<
如何找到他们的最小公倍数?
小数化成分数
写成分母是10,100,1000,……的分数,再化简。
0.25
=
=
分数化成小数
=5÷14≈0.36
分数化成小数,用分子除以分母,除不尽时,要根据需要按“四舍五入”法保留几位小数。
想一想,如何判断一个数能不能化成有限小数?
分母是10,100,1000,……的分数化成小数,可以直接去掉分母,看分母1后面有几个0,就在分子中从最后一位起向左数出几位,点上小数点。
=0.7
=0.39
把小数和相等的分数用线连起来。
0.6 0.03 0.45 3.25 0.18
把下面的分数化成小数(不能化成有限小数的保留两位小数)。
=4÷9≈0.44
=7÷30≈0.23
=5÷6≈0.83
=11÷50=0.22
=0.31
=2÷25=0.8
=23÷20=1.15
做一做,并说说你是怎么想的?
○
○
○
○
<
>
<
>
用分数表示各图中的涂色部分。
8
5
4
7
5
7
在直线上描出表示下面各分数的点。
谢谢聆听
